Феноменологическая модель Рейхардта. Принцип суперпозиции решений

Безуспешные попытки создания общей теории турбулентного движения, даже в рамках несжимаемой жидкости, а также неотложные потребности инженерной практики побудили исследователей заняться построением так называемых феноменологических теорий. Суть этих теорий состоит в том, чтобы, отталкиваясь от экспериментального материала, найти по возможности простые соотношения, генерирующие решения для определенного класса течений.

Наиболее удачная теория такого рода для изобарических турбулентных струй была предложена в 1941 г. Рейхардтом. Он заметил, что распределения скоростей в областях турбулентного перемешивания свободных затопленных струй несжимаемой жидкости достаточно точно описываются уравнениями типа уравнений теплопроводности:

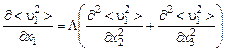, (3.3.1)

где 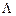– опытный коэффициент, зависящий от продольной координаты.

Формально уравнение Рейхардта (3.3.1) можно получить традиционным методом, осредняя уравнение движения по схеме Рейнольдса.

Покажем это на примере плоской изобарической стационарной струи несжимаемой жидкости.

Запишем уравнение движения струи, отбрасывая члены с молекулярной вязкостью:

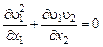. (3.3.2)

После осреднения получим

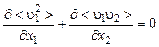. (3.3.3)

Полагая далее, что интенсивность поперечного переноса количества движения пропорциональна поперечному градиенту составляющей количества движения по продольной оси:

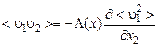, (3.3.4)

приходим к уравнению

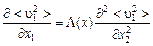, (3.3.5)

которое похоже на уравнение теплопроводности, хотя и сложнее его, так как 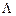зависит от .

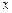В ряде последующих работ метод Рейхардта был обобщен на более сложные типы турбулентных струй: изотермические и неизотермические, затопленные струи и струи, распространяющиеся в спутном потоке, струи с диффузионными факелом горения и т.д. Было показано, что уравнения типа уравнений теплопроводности, записанные в виде

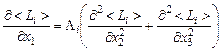, (3.3.6)

позволяют находить распределения газодинамических параметров во всех перечисленных выше случаях. С использованием газодинамических комплексов 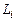автоматически выполняются законы сохранения количества движения, энергии и массы, так как именно эти комплексы входят в интегральные соотношения (3.1.1). Метод Рейхардта, известный в отечественной литературе как метод эквивалентной задачи теории теплопроводности, был обобщен и проверен с привлечением обширного экспериментального материла на различных типах турбулентных струй, в том числе на одиночных и блочных струях, при произвольном профиле распределения параметров в начальном сечении и с учетом возможных физико-химических процессов типа диффузионного горения, диссоциации и ионизации. Накопленный опыт применения уравнений вида (3.3.6) для расчета струйных течений позволяет отметить хорошее соответствие результатов расчета опытным данным.

Наряду с этим многие исследователи обращали внимание на неудовлетворительное физическое обоснование метода Рейхардта. Собственно говоря, сам Рейхардт даже не пытался построить физические модели турбулентного обмена, а ограничился поисками уравнений, которые бы генерировали соответствующие опытным данным распределения газодинамических параметров в турбулентной струе.Такими оказались уравнения типа уравнений теплопроводности. Лишь в дальнейшем появились работы, в которых обсуждался и обосновывался переход от нелинейных дифференциальных уравнений в частных производных пограничного слоя к линейным типа уравнений теплопроводности. В частности, Л.А. Вулис предлагает осуществить такой переход введением некой системы координат, в которой уравнения пограничного слоя преобразуются к виду (3.3.6). Однако предложенная Вулисом модель носит формальный характер и не объясняет физическую сущность процессов, протекающих в струйном пограничном слое.

Причину хорошего соответствия решений уравнений типа уравнений теплопроводности для математических ожиданий комплексов 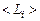опытным данным следует искать в вероятностном характере турбулентного движения.

Действительно, решения уравнений типа уравнений теплопроводности для комплексов 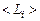удовлетворяют следующим условиям.

1. На больших расстояниях от начального сечения изобарического участка турбулентной струи 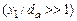распределения комплексов 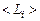по сечениям приближаются к распределениям, даваемым нормальным законом.

2. Справедлив принцип суперпозиции частных решений для комплексов 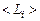(см. формулу (3.1.5)). Принцип суперпозиции частных решений вытекает из линейности уравнений (3.3.6).

Можно показать, что оба сформулированных утверждения непосредственно следуют из известных теорем теории вероятности, если принять во внимание случайный характер движения элементарных масс при переносе их крупномасштабными пульсациями. Так как отклонение каждой такой элементарной массы от линии, параллельной оси струи, – случайная величина, то его можно статистически описать, задав соответствующую плотность вероятности. Из центральной предельной теоремы теории вероятности следует, что после достаточно большого числа пульсаций плотность вероятности отклонения элементарной массы от математического ожидания будет характеризоваться нормальным законом. Если далее предположить, что каждой такой элементарной массе соответствует определенное значение 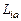, то, по определению математического ожидания случайной величины, придем к первому утверждению. Второе утверждение является следствием теоремы о математическом ожидании суммы случайных величин.

Обратим внимание на следующие два важных момента:

1. Задаваемые в интегральном методе расчета турбулентных струй распределения математических ожиданий комплексов 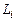в виде соотношений (3.1.3) и (3.1.5) являются решениями уравнений типа уравнений теплопроводности, что легко проверить непосредственной подстановкой этих соотношений в (3.3.6).

2. Линейный характер уравнений типа уравнений теплопроводности позволяет получать аналитические решения на изобарических участках двумерных и трехмерных струй при произвольной форме границы начального сечения и в общем случае неравномерном распределении в нем газодинамических параметров. Поэтому время, затрачиваемое на расчет параметров в струе при использовании полуэмпирической теории турбулентности Рейхардта, существенно меньше, чем при применении других полуэмпирических моделей, оперирующих с нелинейными дифференциальными уравнениями в частных производных. Это обстоятельство и обусловило широкое использование метода Рейхардта в инженерной практике при расчете струйных течений.