Теорема сложения ускорений
В случае непоступательного переносного движения абсолютное ускорение точки равно геометрической сумме переносного, относительного и ускорения Кориолиса.
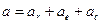
Поворотным ускорением (ускорением Кориолиса) называется составляющая абсолютного ускорения точки в составном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки:
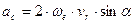
где 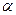 - угол между вектором относительной скорости и осью вращения в переносном движении.
- угол между вектором относительной скорости и осью вращения в переносном движении.
Направление ускорения Кориолиса находится по правилу: Относительную скорость точки следует спроектировать на плоскость, перпендикулярную оси переносного вращения, и повернуть эmy проекцию в той же плоскости на 90°, в сторону переносного вращения.
Ускорение Кориолиса равно нулю в трех случаях:
1) если 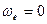 , т.е. в случае поступательного переносного движения.
, т.е. в случае поступательного переносного движения.
2) если 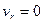 , т.е. в случае относительного покоя точки или в моменты обращения в нуль относительной скорости движущейся точки;
, т.е. в случае относительного покоя точки или в моменты обращения в нуль относительной скорости движущейся точки;
3) если 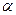 =90º вектор относительной скорости перпендикулярен оси вращения в переносном движении.
=90º вектор относительной скорости перпендикулярен оси вращения в переносном движении.
Пример 1
Вертикальный подъем вертолета происходит согласно уравнению 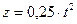 При этом уравнение вращения винта имеет вид
При этом уравнение вращения винта имеет вид 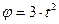 .Определить абсолютные скорость и ускорение точки винта, отстоящей на расстоянии
.Определить абсолютные скорость и ускорение точки винта, отстоящей на расстоянии 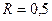 мот вертикальной оси вращения, в конце 5-й с.
мот вертикальной оси вращения, в конце 5-й с.
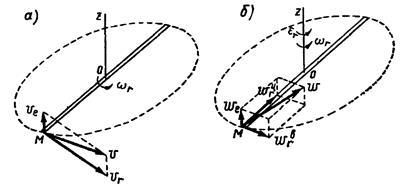
Свяжем подвижную систему отсчета с корпусом вертолета, неподвижную - с Землей.
Относительное движение - вращение винта вокруг его оси является (это движение наблюдает пассажир вертолета, связанный с подвижной системой отсчета).
Переносное движение - является поступательное движение вертолета вертикально вверх.
Применяем теорему о сложении скоростей
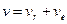
Относительная скорость точки М является окружной скоростью винта вертолета и определяется из соотношения
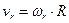
Если известен закон вращения винта 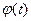 , то угловая скорость определится как первая производная от этого закона движения
, то угловая скорость определится как первая производная от этого закона движения
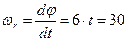 с-1
с-1
Тогда
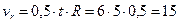 м/с
м/с
Вертолёт совершает поступательное движение. Переносная скорость точки М является скоростью движения вертолета вверх, зная закон движения которого определим
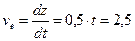 м/с
м/с
Так как 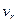 ┴
┴ 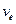 то
то
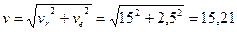 м/с
м/с
Применяем теорему о сложении ускорений
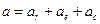
Винт совершает вращательное движение. Следовательно относительное ускорение точки М винта определяется как ускорение точки вращающегося тела.
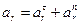
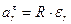
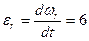 с-2
с-2
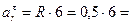 3 м/с2
3 м/с2
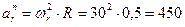 м/с2
м/с2
Переносная скорость точки М является скорости движения вертолета вверх.
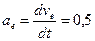 м/с2
м/с2
Ускорение Кориолиса равно нулю так как Вертолёт совершает поступательное движение ( 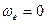 ):
):
Так как 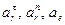 взаимно перпендикулярны, то
взаимно перпендикулярны, то
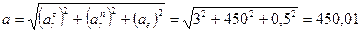 м/с2
м/с2
Пример 2
Диск равномерно вращается с угловой скоростью 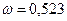 с-1. По диску из его центра по желобу движется точка M, по закону движения
с-1. По диску из его центра по желобу движется точка M, по закону движения 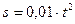 , определить абсолютную скорость и ускорения точки через 2 с после начала движения.
, определить абсолютную скорость и ускорения точки через 2 с после начала движения.
Относительное движение – движение точки по желобу.
Переносное движение – вращение диска.
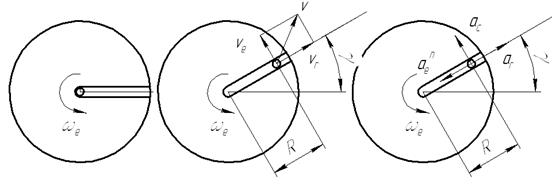
Определение положения точки
Определим, на какое расстояние переместится точка за время t по желобу
 м
м
Определим, на какой угол повернется желоб за время t
Если тело вращается равномерно, то за 1 сек тело повернется на 1 радиан (57,32º), тогда за 0,523 с тело повернется на 0,523 рад или 57,32·0,523 = 30º
Покажем на рисунке положение точки в момент времени t = 0,523 с.
Применяем теорему о сложении скоростей
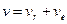
Относительную скорость точки М определим зная закон движения по желобу
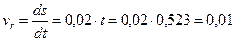 м/с
м/с
Переносная скорость точки М является окружной скоростью.
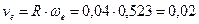 м/с
м/с
Так как 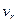 ┴
┴ 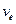 то
то
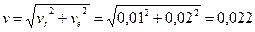 м/с
м/с
Применяем теорему о сложении ускорений
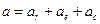
Относительное ускорение точки М определим зная закон движения по желобу
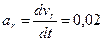 м/с2
м/с2
Переносное ускорение точки М складывается для вращательного движения из нормального и тангенциального ускорений.
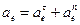
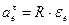
Так как тело движется с постоянной угловой скоростью 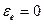 следовательно
следовательно 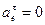
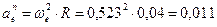 м/с2
м/с2
Ускорение Кориолиса:
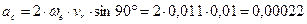 м/с2
м/с2
Абсолютное ускорение
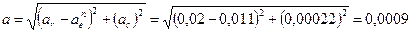 м/с2
м/с2
Дата добавления: 2018-11-25; просмотров: 1018;
