Метод Фурье для уравнения свободных колебаний струны
Метод Фурье или метод разделения переменных является одним из наиболее распространенных методов решения уравнений в частных производных. Изложение этого метода мы проведем для задачи о свободных колебаниях струны, закрепленной на концах. Эта задача, как было показано в п. 1.24, сводится к решению однородного уравнения
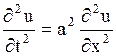
| (1.132) |
при однородных граничных условиях
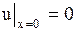 , , 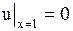
| (1.133) |
и начальных условиях
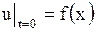 , , 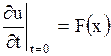 , , 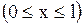 . .
| (1.134) |
Выделим две части метода Фурье. Первая часть заключается в отыскании частных решений уравнения (1.132), удовлетворяющих граничным условиям (1.133). Вторая часть - нахождение общего решения и удовлетворение начальным условиям (1.134).
Будем искать частные решения (1.132), не равные тождественно нулю, в виде произведения двух функций
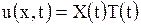 , ,
| (1.135) |
удовлетворяющие граничным условиям (1.133).
Дифференцируя дважды выражение (1.135) по 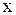 и по
и по 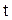 , получим
, получим
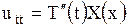 ,
, 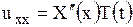 .
.
Подставляя найденные производные в уравнение (1.132), получим
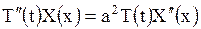
или, деля обе части равенства на 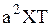 ,
,
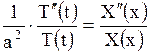 .
.
Последнее равенство, левая часть которого зависит от 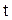 , а правая - только от
, а правая - только от 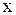 , возможно лишь в том случае, когда обе части его не зависят ни от
, возможно лишь в том случае, когда обе части его не зависят ни от 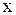 ни от
ни от 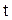 , т.е. представляют собой одну и ту же постоянную. Обозначим эту постоянную через
, т.е. представляют собой одну и ту же постоянную. Обозначим эту постоянную через 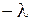 (Знак числа
(Знак числа 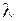 будет обоснован ниже). Итак, имеем
будет обоснован ниже). Итак, имеем
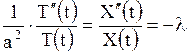 . .
| (1.136) |
Из равенства (1.136) получим два обыкновенных дифференциальных уравнения
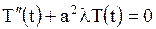 , ,
| (1.137) |
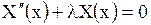 . .
| (1.138) |
Таким образом, уравнение (1.132) распалось на два уравнения, из которых одно содержит функцию только от 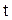 , а другое - функцию только от
, а другое - функцию только от 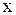 или, как говорят, в уравнении (1.132) переменные разделились.
или, как говорят, в уравнении (1.132) переменные разделились.
Поскольку мы ищем решения вида (1.135), удовлетворяющие граничным условиям (1.133), то при любом значении 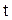 должны соблюдаться равенства
должны соблюдаться равенства
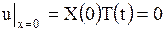 ,
, 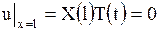 .
.
Если бы обращался в нуль второй сомножитель ( 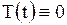 ), то функция
), то функция 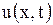 равнялась бы нулю при всех значениях
равнялась бы нулю при всех значениях 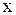 и
и 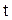 . Такой случай интереса не представляет. Поскольку мы ищем нетривиальные решения, т.е. не равные тождественно нулю, то мы должны считать, что
. Такой случай интереса не представляет. Поскольку мы ищем нетривиальные решения, т.е. не равные тождественно нулю, то мы должны считать, что
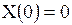 и и 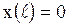 . .
| (1.139) |
Для определения функции 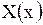 мы пришли к следующей краевой задаче для обыкновенного дифференциального уравнения: найти такие значения параметра
мы пришли к следующей краевой задаче для обыкновенного дифференциального уравнения: найти такие значения параметра 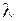 , при которых существуют нетривиальные решения уравнения (1.138), удовлетворяющие граничным условиям (1.139). Эту задачу называют задачей Штурма-Лиувилля.
, при которых существуют нетривиальные решения уравнения (1.138), удовлетворяющие граничным условиям (1.139). Эту задачу называют задачей Штурма-Лиувилля.
Те значения параметра 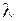 , при которых задача (1.138) - (1.139) имеет нетривиальные решения, называются собственными значениями, а сами эти решения - собственными функциями.
, при которых задача (1.138) - (1.139) имеет нетривиальные решения, называются собственными значениями, а сами эти решения - собственными функциями.
Найдем теперь собственные значения и собственные функции задачи (1.138) - (1.139). Нужно рассмотреть три случая, когда 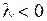 ,
, 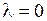 и
и 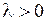 .
.
Уравнение (1.138) есть линейное однородное уравнение 2-го порядка с постоянными коэффициентами. Для его решения надо составить характеристическое уравнение
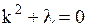 ;
;
отсюда 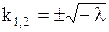 , следовательно, вид решения зависит от знака
, следовательно, вид решения зависит от знака 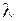 .
.
А. Пусть 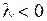 . Тогда корни характеристического уравнения действительны и различны и общее решение уравнения (1.138) имеет вид
. Тогда корни характеристического уравнения действительны и различны и общее решение уравнения (1.138) имеет вид
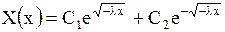 .
.
Удовлетворяя граничным условиям (1.139), получим
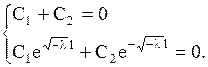
Так как определитель этой однородной системы
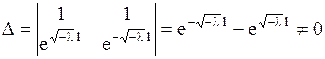 ,
,
то, как известно, система имеет единственное решение 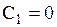 и
и 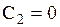 . Следовательно,
. Следовательно, 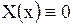 .
.
Таким образом, в этом случае решений, отличных от нуля, не существует.
Б. Пусть 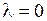 . Тогда оба корня характеристического уравнения равны нулю и
. Тогда оба корня характеристического уравнения равны нулю и
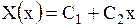 .
.
Граничные условия (1.139) дают:
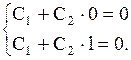
Отсюда 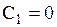 ,
, 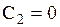 и, следовательно,
и, следовательно, 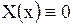 .
.
В. Пусть 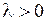 . Корни характеристического уравнения мнимые (
. Корни характеристического уравнения мнимые ( 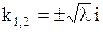 ) и решение уравнения (1.138) имеет вид
) и решение уравнения (1.138) имеет вид
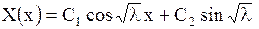 .
.
Удовлетворяя условиям (1.139), получим
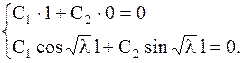
Из первого уравнения следует, что 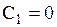 , а из второго следует, что
, а из второго следует, что 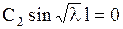 . Последнее равенство возможно, когда
. Последнее равенство возможно, когда 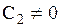 , ибо в противном случае
, ибо в противном случае 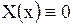 . Поэтому
. Поэтому
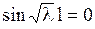 ,
,
откуда определяем 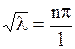 , где
, где 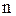 - любое целое число
- любое целое число 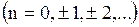 .
.
Следовательно, нетривиальные решения задачи (1.138) - (1.139) возможны лишь при значениях
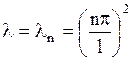 . .
| (1.140) |
Решение, отвечающее фиксированному значению 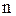 , обозначим через
, обозначим через 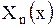 . Оно имеет вид
. Оно имеет вид
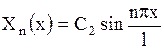 .
.
Для дальнейшего можем положить 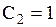 .
.
Итак, собственным значениям 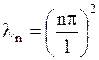 соответствуют собственные функции
соответствуют собственные функции
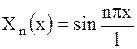 , , 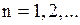 . .
| (1.141) |
Заметим, что в соотношениях (1.140), (1.141) мы ограничились только положительными значениями для 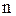 , так как отрицательные значения
, так как отрицательные значения 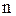 не дают новых решений.
не дают новых решений.
Обратимся теперь к отысканию функций 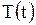 . Каждому собственному числу
. Каждому собственному числу 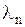 будет соответствовать свое решение уравнения (1.137), которое обозначим через
будет соответствовать свое решение уравнения (1.137), которое обозначим через 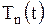 . Для функции
. Для функции 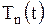 имеем уравнение
имеем уравнение
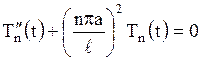 .
.
Общее решение этого уравнения имеет вид
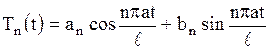 ,
,
где 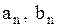 - произвольные постоянные.
- произвольные постоянные.
Таким образом, функция
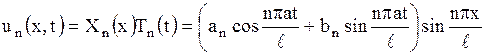 , ,
| (1.142) |
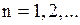 , удовлетворяет уравнению (1.132) и граничным условиям (1.133) при любых
, удовлетворяет уравнению (1.132) и граничным условиям (1.133) при любых 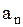 и
и 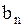 .
.
Перейдем ко второй части метода Фурье.
При помощи собственных функций построим решения, удовлетворяющие начальным условиям (1.134).
Возьмем общее решение уравнения (1.142) в виде ряда
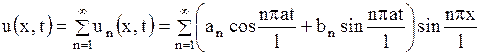 . .
| (1.144) |
Если ряд (1.144) сходится равномерно в области 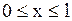 ,
, 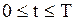 , то сумма его является непрерывной функцией в этой области. В силу однородности и линейности уравнения (1.132) ряд (1.144) будет также решением, если его можно почленно дифференцировать по
, то сумма его является непрерывной функцией в этой области. В силу однородности и линейности уравнения (1.132) ряд (1.144) будет также решением, если его можно почленно дифференцировать по 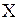 и по
и по 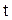 . Действительно, при указанных условиях получим
. Действительно, при указанных условиях получим
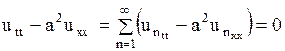 ,
,
так как функции 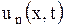 удовлетворяют уравнению (1.132).
удовлетворяют уравнению (1.132).
Далее, поскольку каждое слагаемое в (1.144) удовлетворяет граничным условиям (1.133), то этим условиям будет удовлетворять и сумма ряда, т.е. функция 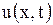 . Остается определить постоянные
. Остается определить постоянные 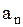 и
и 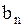 так, чтобы функция (1.144) удовлетворяла начальным условиям.
так, чтобы функция (1.144) удовлетворяла начальным условиям.
Продифференцируем ряд (1.144) по 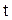 :
:
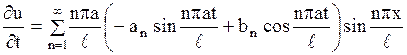 . .
| (1.145) |
Подставляя 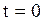 в (1.144) и (1.145), получим в силу начальных условий (1.134):
в (1.144) и (1.145), получим в силу начальных условий (1.134):
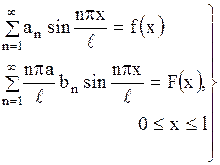
| (1.146) |
Формулы (1.146) представляют собой разложение заданных функций 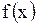 и
и 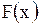 в ряд Фурье по синусам на интервале
в ряд Фурье по синусам на интервале 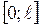 .
.
Из теории рядов Фурье известно, что всякая функция 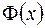 , непрерывная на отрезке
, непрерывная на отрезке 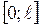 вместе со своей производной первого порядка и удовлетворяющая условию
вместе со своей производной первого порядка и удовлетворяющая условию 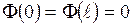 , разлагается в абсолютно и равномерно сходящийся ряд Фурье по синусам:
, разлагается в абсолютно и равномерно сходящийся ряд Фурье по синусам:
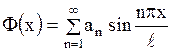 ,
,
где
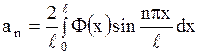 .
.
Предполагая, что функции 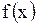 и
и 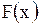 удовлетворяют указанным условиям, мы можем утверждать, что
удовлетворяют указанным условиям, мы можем утверждать, что 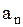 и
и 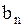 - коэффициенты Фурье, которые вычисляются по известным формулам:
- коэффициенты Фурье, которые вычисляются по известным формулам:
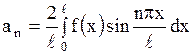 , ,
| (1.147) |
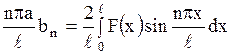 ,
,
откуда
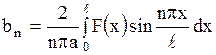 . .
| (1.148) |
Таким образом, ряд (1.144), в котором 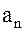 и
и 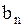 вычисляются по формулам (1.147), (1.148), дает решение смешанной краевой задачи (1.132)…(1.134).
вычисляются по формулам (1.147), (1.148), дает решение смешанной краевой задачи (1.132)…(1.134).
Дата добавления: 2018-11-25; просмотров: 362;
