Коэффициент корреляции и гипотеза о значимости связи.

Коэффициент корреляции между случайными переменными X и Y определяется как

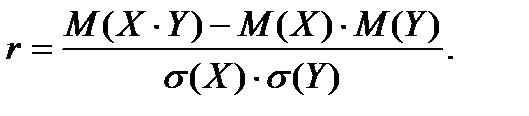
Его оценкой является выборочный коэффициент корреляции, который можно вычислить как:

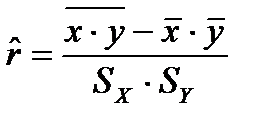, где

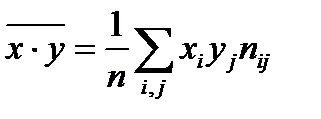– выборочное среднее произведение величин Х и Y,

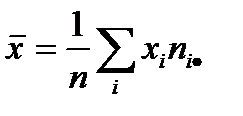– выборочное среднее значение случайной величины Х,

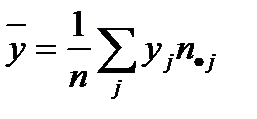– выборочное среднее значение случайной величины Y,

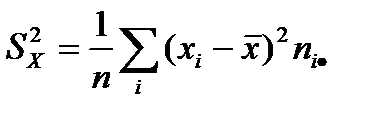– выборочная дисперсия случайной величины Х,

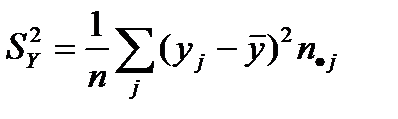– выборочная дисперсия случайной величины Y,

Выборочный коэффициент корреляции обладает свойствами, аналогичными свойствам теоретического коэффициента корреляции:

1) Коэффициент корреляции принимает значения из промежутка [-1; 1]

.

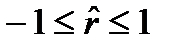2) Если переменные Х и Y умножить на одно и то же число, то коэффициент корреляции не измениться.

3) Если 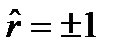, то корреляционная связь между переменными представляет собой линейную зависимость.

После вычисления выборочного коэффициента корреляции проверяют гипотезу о значимости связи, так как выборочный коэффициент корреляции, как правило, не совпадает с теоретическим коэффициентом корреляции и может не равняться нулю из–за отбора переменных в выборку.

Обычно проверяется основная гипотеза об отсутствии корреляционной связи.

Н₀: r = 0 против альтернативы Н₁: r ¹ 0.

В случае справедливости основной гипотезы Н₀ статистика

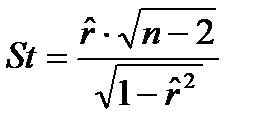
имеет распределение Стьюдента с n-2 степенями свободы.

Считают, что выборочный коэффициент корреляции значимо отличается от нуля, если значение статистики по модулю больше критического

,

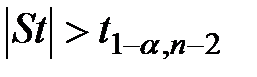где 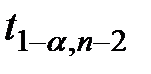- критическое значение распределения Стьюдента, определённое на уровне значимости a при числе степеней свободы, равном n-2 (т.е. квантиль уровня 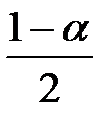распределения Стьюдента с n-2 степенями свободы).