Основы теории кодирования

Кодомназывается система условных знаков (символов), для передачи, обработки и хранения информации.

Пусть А – произвольный алфавит. Элементы алфавита А называются буквами, а конечные вектора, составленные из букв – словами.

Длина слова – число букв в слове 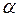, обозначается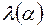

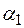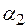Соединение слов и обозначим через 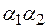, а соединение n одинаковых слов 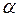– через 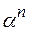. Слово 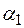называется началом слова 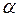, если существует слово 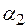, такое что .

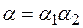Рассмотрим алфавит .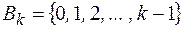

Произвольное отображение произвольного множества М в множество слов в алфавите 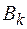называется k-ичным кодированием множества М.

При k = 2, 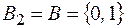– двоичное множество.

Пример 1.

Кодирование (отображение) Е – двоичная запись натуральных чисел с помощью минимального количества букв.

Числу 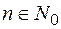ставится в соответствие слово

,

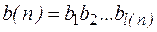наименьшей длины, удовлетворяющее условию:

.

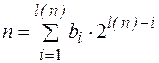При этом 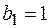, а длина слова 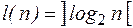. Последнее условие означает, что n удовлетворяет неравенству

.

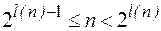Пусть n = 12.

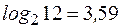, т. е. это дробное число между 3 и 4. Инкремент этого логарифма равен 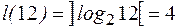, так как это следующее целое, идущее за ним.

Аналогично 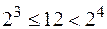. Значит, .

.

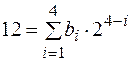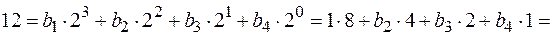
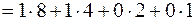Таким образом, двоичный код числа 12 имеет вид:

.

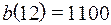Пример 2.

Кодирование 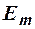– двоичная запись натуральных чисел с помощью m букв.

Числу 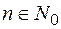, удовлетворяющему условию

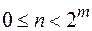
ставится в соответствие слово

.

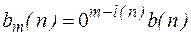Пусть n = 12, m = 3.

Так как неверно то, что 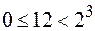, то это означает, что код 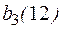построить невозможно.

Пусть n = 12, m = 6.

Так как верно то, что 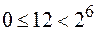, то это означает, что код 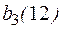построить можно, его вид:

.

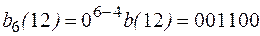Побуквенное кодирование – это кодирование слов в алфавите А таким образом, что сначала кодируются буквы алфавита 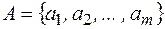двоичными словами из множества кодовых слов 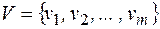, а затем уже слово, составленное в алфавите А заменяется последовательностью кодовых слов, соответствующих его буквам. Пример побуквенного кодирования слов – азбука Морзе.

Код называется разделимым, если разным словам в алфавите А всегда соответствуют разные слова в алфавите V.

Утверждение 1.

Побуквенное кодирование является взаимно однозначным тогда и только тогда, когда оно задается с помощью разделимого кода.

Равномерный код – это код, в котором все кодовые слова имеют одинаковую длину.

Утверждение 2.

Равномерный код всегда разделим.

Код называется префиксным, если никакое кодовое слово из V не является началом другого кодового слова.

Утверждение 3.

Префиксный код всегда является разделимым, но разделимый код не обязательно является префиксным. Т. е. префиксность является достаточным условием разделимости, но не является необходимым условием.

Пусть источник случайным образом генерирует буквы алфавита 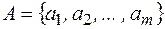, причем вероятность появления каждой буквы известна. Таким образом задано распределение вероятностей Р вида:

			…
			…

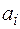
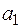
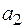
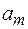
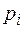
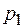
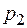
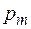
Так как алфавит фиксирован, то это распределение можно записать в виде: .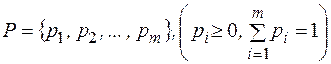

Стоимостью кода V при распределении P назовем число

.

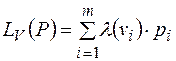Оно характеризует среднее количество букв кодирующих слов, приходящихся на одну букву алфавита А при кодировании V. Очевидно, что при различных кодированиях одного и того же алфавита, стоимость кодов будет различной.

Префиксный код 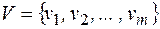называется оптимальным при распределении 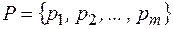, если его стоимость минимальна по сравнению с другими кодами алфавита А при распределении Р.

Пример 3.

Код Р. Фано, близкий к оптимальному, заключается в следующем. Упорядоченный (в порядке не возрастания вероятностей) список букв алфавита делится на две последовательные части так, чтобы суммы вероятностей входящих в них букв отличались как можно меньше. Буквам из 1-ой части присваивается символ 0, из 2-ой – 1. С каждой частью поступают аналогично. Так делается пока, в каждой из частей не окажется по одной букве. Полученные последовательности нулей и единиц является кодом Фано данного алфавита.

В таблице приведен пример построения кода Фано для распределения Р = {0.30, 0.18, 0.14, 0.14, 0.11, 0.06, 0.05, 0.02}.

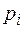
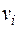
a		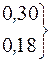0,48	0,30
b	0,18
c		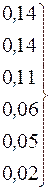0,52		0,28	0,14
d	0,14
e		0,24		0,11
f		0,13		0,06
g		0,07	0,05
h	0,02

Найдем стоимость полученного кода.

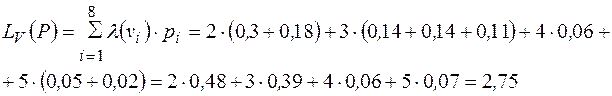
Теорема Хаффмена

Если 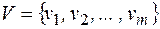– оптимальный двоичный код при распределении 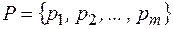, и некоторая вероятность 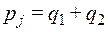, причем

,

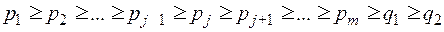то код 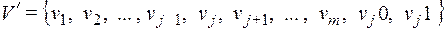так же является оптимальным при распределении

.

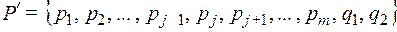Код 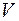является расширением кода .

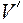Пример 4.

Построение оптимального кода Хаффмена заключаются в следующем. Пусть в упорядоченном по невозрастанию вероятностей списке две последние вероятност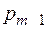и и 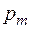. Эти вероятности из списка исключаются, а их сумма вставляется в список таким образом, чтобы вероятности по-прежнему не убывали. Делаем так, пока в списке не останется две вероятности. Первой из них присваивается символ 0, второй – символ 1. Получаем оптимальный код, состоящий из 2 кодовых слов. Далее, используя теорему расширяем его до кода из 3 слов, и т. д. Пока не получим список исходных вероятностей.

Ниже приведен пример построения кода Хаффмена для распределения Р = {0.5, 0.2, 0.2, 0.1}.

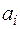
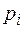
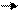
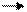
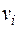
a	0,5		0,5		0,5
b	0,2		0,3		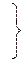0,5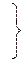
c	0,2		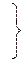0,2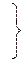
d	0,1

Найдем стоимость полученного кода.

.

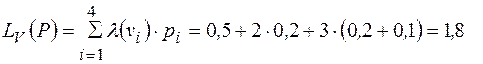Рассмотрим равномерный код с обнаружением и исправлением ошибок.

Однозначной ошибкойтипазамещения называют результат замены одного из символов 0 на 1 или 1 на 0. Кратностью ошибки s называется число ошибок одного типа. Например, если передаваемое слово 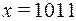, а на приемной станции получено 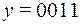, то в слове произошла ошибка типа замещения.

Функция Хемминга 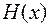, задается на двоичных векторах 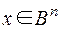. Это вектор минимальной длины l, полученный в результате покоординатного сложения по модулю 2 двоичных кодов номеров тех координат вектора х, которые равны 1.

Здесь l – та длина двоичного кода, которой достаточно, чтобы закодировать номера всех координат слова х.

.

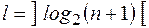Таким образом,

.

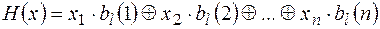Пример 5.

Найти функцию Хемминга для двоичного слова 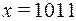. Так как 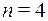, то 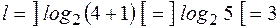. Найдем двоичные коды длины 3 для всех номеров координат слова х .

n

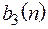
Тогда = =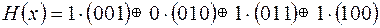

= = .

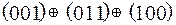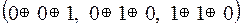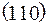Кодом Хемминга называется подмножество двоичных слов 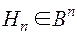, для каждого из которых функция Хемминга равна нулевому вектору. Таким образом .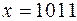

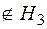Утверждение.

Количество двоичных слов 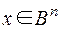, принадлежащих коду Хемминга равно .

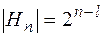Теорема Хемминга

Код Хемминга является кодом с исправлением одного замещения.

Пример 6.

Пусть при передаче по каналу связи в двоичном слове 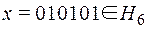произошло замещение 5-ого символа, в результате чего получилось слово 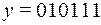. Найдем функцию Хемминга 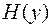. . 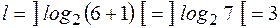Сложим по модулю 2 двоичные коды номеров только тех координат вектора у, которые равны 1.

.

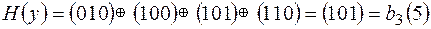Полученный результат является двоичным кодом номера того места, на котором произошло замещение.