АЛГЕБРА ЛОГИЧЕСКИХ ФУНКЦИЙ
Основные определения
Двоичное (бинарное) множество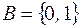 
, где логический символ 0 означает – «ложь», логический символ 1 означает – «истина».
Логической функцией называется операция типа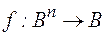 
. 
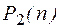– множество всех логических функций от n переменных. 
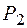– множество всех логических функций.
Утверждение:
.
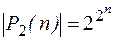Единичным набором значений аргументов называется набор, на котором функция равна 1. Множество единичных наборовфункции f называется единичным множеством –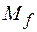 
.
Нулевым набором значений аргументов называется набор, на котором функция равна 0. Множество нулевых наборовфункции f называется нулевым множеством –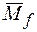 
.
Таблица логических функций одной переменной
| х |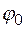 
| 
| 
| 
|
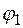
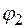
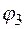
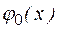= 0 – функция-константа 0;
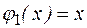– тождество переменной х;
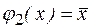– отрицание переменной х;
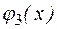= 1 – функция-константа 1.
Таблица логических функций двух переменных
| x | y | ||||||||
| x | y | ||||||||
Функции № 0 и № 15 – функции константы 0 и 1.
Константы принимают одно и то же значение при любых наборах значений аргументов.
Функция № 1 – конъюнкция x и y. Обозначение конъюнкции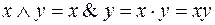 
. Конъюнкция принимает значение 1 только в случае, когда и х и у равны 1.
Функция № 7 – дизъюнкция x и y. Обозначение дизъюнкции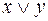 
. Дизъюнкция принимает значение 1 тогда, когда х или у равны 1 (т.е. хотя бы один аргумент).
Функция № 9 – эквивалентность x и y. Обозначение эквивалентности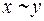 
. Эквивалентность принимает значение 1 только в случае, когда х и у равны.
Функция № 6 – сложение по модулю 2 x и y. Обозначение сложения по модулю 2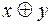 
. Сложение по модулю 2 принимает значение 1 только в случае, когда сумма х и у нечетна.
Функция № 13 – импликация x и y. Обозначение импликации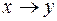 
. Импликация принимает значение 0 только в случае, когда из «истины» следует «ложь».
Функция № 11 – импликация у и х. Обозначение –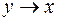 
.
Функция № 14 – штрих Шеффера x и y. Обозначение штриха Шеффера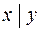 
. Штрих Шеффера является отрицанием конъюнкции: 
.
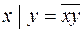Функция № 8 – стрелка Пирса x и y. Обозначение стрелки Пирса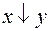 
. Стрелка Пирса является отрицанием дизъюнкции: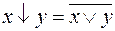 
Введем обозначения:
; 
.
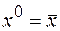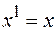Дата добавления: 2018-09-24; просмотров: 1418;