Второе начало термодинамики
Анализ работы идеальной тепловой машины по циклу Карно, показал, что коэффициент полезного действия h, не зависит от природы рабочего тела, а определяется только температурным интервалом, в котором совершается работа (теорема Карно-Клаузиуса):
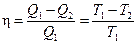 или
или 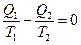 ,
,
где Q1 – количество теплоты, сообщенное рабочему телу при температуре T1; Q2 – количество теплоты, отданное рабочим телом при температуре T2.
Если представить цикл Карно суммой бесконечно малых циклов, в каждом из которых 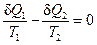 , то в циклическом процессе
, то в циклическом процессе 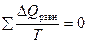 , а это значит, что интеграл, взятый по замкнутому контуру, равен нулю:
, а это значит, что интеграл, взятый по замкнутому контуру, равен нулю: 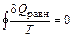 . Следовательно, подынтегральная функция
. Следовательно, подынтегральная функция 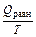 является функцией состояния. Эту функцию Рудольф Клаузиус (Clausius) назвал энтропией (S) (entropia — превращение).
является функцией состояния. Эту функцию Рудольф Клаузиус (Clausius) назвал энтропией (S) (entropia — превращение).
Для обратимого (равновесного) процесса изменение энтропии равно:
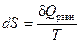 ,
, 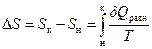 .
.
Для необратимого (неравновесного) процесса, как было показано на примере расширения идеального газа, работа, производимая системой в самопроизвольном процессе, меньше работы, производимой в равновесном процессе: Wнеравн< Wравн. Принимая во внимание первое начало термодинамики dU =dQ + dW и учитывая, что внутренняя энергия – функция состояния (dUравн=dUнеравн), получаем, что dQнеравн >dQравн. Соответственно для необратимого (неравновесного) процесса изменение энтропии 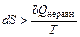 .
.
В общем случае для любого процесса можно написать:
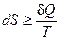 ,
, 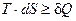 .
.
Знак равенства относится к равновесным процессам, знак неравенства – к неравновесным.
Согласно первому началу термодинамики dQ = dU + p×dV, следовательно, T×dS ³ dU + p×dV. В изолированной системе dU = dV =0, а так как Т >0, то dS ³0.
Второе начало термодинамики утверждает, что в изолированной системе самопроизвольно протекают процессы с увеличением энтропии, которые прекращаются при достижении ее максимального значения, соответствующего состоянию термодинамического равновесия.
Энтропия играет большую роль во всех процессах в природе, в частности является одним из факторов, определяющих направление самопроизвольного протекания химических реакций и достижения равновесия в системах.
Энтропия
Физический смысл энтропии раскрывает статистическая физика, рассматривая энтропию как меру вероятности пребывания системы в данном термодинамическом состоянии (принцип Больцмана). Величина энтропии пропорциональна термодинамической вероятности состояния системы.
Состояние термодинамической системы характеризуется набором термодинамических параметров и функций. Их значения характеризуют макросостояние системы и не связаны с положением отдельных частиц в пространстве и их энергией. Таким образом, макросостояние характеризует совокупность взаимодействующих частиц, систему в целом. Очевидно, что конкретное макросостояние может быть реализовано при различном положении отдельных частиц в пространстве и их энергии, варианты которых соответствуют микросостояниям системы. Таким образом, конкретному макросостоянию системы соответствует набор ее микросостояний.
Термодинамическая вероятность (w) состояния системы определяется числом микросостояний, которым можно реализовать данное макросостояние:
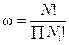 ,
,
где N – число энергетических состояний; Ni – число частиц с данной энергией.
Таким образом,термодинамическая вероятность, в отличие от математической, не может быть меньше единицы (w ³ 1).
Пример.Система состоит из трех частиц: a, b, c. Частицы могут находиться в трех энергетических состояниях: 1, 2, 3. Система может находиться в различных макросостояниях, которые могут быть реализованы различными способами.
1) Первое макросостояние. Все три частицы находятся в первом энергетическом состоянии:
| a, b, c | - | - |
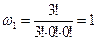 ; (0! = 1).
; (0! = 1).
Данное макросостояние реализуется единственным способом.
2) Второе макросостояние. Две частицы – в первом, а третья – во втором энергетических состояниях:
| a, b | c | - |
| a, c | b | - |
| b, c | a | - |
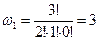 .
.
Данное макросостояние реализуется тремя способами.
3) Третье макросостояние. Все частица находятся в разных энергетических состояниях:
| a | b | c |
| a | c | b |
| b | a | c |
| a | a | b |
| b | c | a |
| c | b | a |
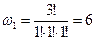 .
.
Данное макросостояние реализуется шестью способами.
Термодинамическая вероятность системы связана с ее энтропией уравнением Больцмана (Boltzmann):
S = k×lnw,
где k = 1,38×10-23Дж/К – константа Больцмана (k = R/NА); w – термодинамическая вероятность состояния системы.
Величина энтропии является количественной характеристикой степени упорядоченности системы: чем более упорядочена система, тем меньше вариантов микросостояний, которыми может быть реализовано ее состояние.
Статистическое толкование понятия энтропия позволяет иным образом сформулировать второе начало термодинамики. В изолированной системе самопроизвольно будут протекать процессы с увеличением термодинамической вероятности, а состояние равновесия соответствует состоянию с максимальной вероятностью.
Очевидно, что из трех рассмотренных в примере макросостояний системы третье наиболее вероятно. Необходимо отметить, что рассматриваемая система, состоящая из трех частиц, приведена исключительно для иллюстрации понятия "термодинамическая вероятность". В реальных системах анализируемое число частиц должно быть достаточно велико (статистически значимо).
Можно определить абсолютное значение энтропии веществ, поскольку известно состояние системы с нулевым значением энтропии. Энтропия идеального кристалла при 0 К равна нулю (постулат Планка – третье начало термодинамики). Поэтому энтропия любого вещества, простого или сложного, является абсолютной и всегда имеет положительное значение.
Размерность величины энтропии [Дж/К]. Энтропия одного моля вещества в стандартных термодинамических условиях S0298 [Дж/моль×К] называется стандартной энтропией вещества, ее значения для различных веществ приведены в справочной литературе (термодинамические характеристики веществ).
Рассмотрим факторы, влияющие на величину энтропии.
Изменение энтропии при фазовых превращениях (плавление↔кристаллизация – DmH; испарение↔конденсация – DvH; полиморфные превращения кристаллов):
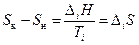 .
.
DiH и Ti – соответственно энтальпия и температура фазового перехода. Энтропия в результате фазового перехода от низкотемпературной фазы к высокотемпературной растет (DiS>0), при обратном переходе уменьшается на ту же величину (DiS<0). Поэтому стандартная энтропия вещества в кристаллическом состоянии меньше, чем в жидком, а в жидком меньше, чем в газообразном. Данный факт очевиден: чем меньше упорядоченность системы, тем энтропия больше. В ряду "кристалл, жидкость, газ" упорядоченность уменьшается.
Пример.
| Фаза | лед | жидкая вода | водяной пар |
| S0298, Дж/моль×К | 39,33 | 69,95 | 188,72 |
| Фаза | углерод (алмаз) | углерод (графит) |
| S0298, Дж/моль×К | 2,37 | 5,74 |
Состав и структура молекул. С усложнением молекулы уменьшается упорядоченность системы, поэтому 1 моль вещества, образованного более сложными молекулами, имеет бόльшую величину энтропии.
Пример.
| Кислород (газ) | атомарный (О) | молекулярный (О2) | озон (О3) |
| S0298, Дж/моль×К | 160,95 | 205,04 | 238,82 |
Температура. Увеличение температуры всегда приводит к росту энтропии. Температура является характеристикой (мерой) теплового движения молекул и атомов. Поэтому с ростом температуры растет интенсивность движения частиц и соответственно уменьшается упорядоченность системы:
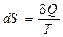 ,
, 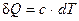 →
→ 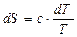 .
.
При нагревании в изобарных условиях (при постоянном давлении) изменение энтропии
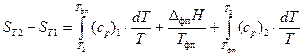 .
.
Если в температурный интервал Т1–Т2 попадают фазовые переходы (плавление↔кристаллизация; испарение↔конденсация; полиморфные превращения кристаллов), то при температуре фазового перехода Тфп энтропия вещества изменяется скачком на величину DфпH/Тфп (DфпH – энтальпия фазового перехода). Меняется скачком и теплоемкость вещества (ср – изобарная теплоемкость соответствующей фазы).
Изменение энтропии при протекании химических реакций. Поскольку энтропия является функцией состояния, то ее изменение при протекании химическойреакции равно разности между суммой энтропий продуктов реакции и суммой энтропий исходных веществ (с учетом числа молей веществ). Часто приводят изменение энтропии в ходе реакции для стандартных условий:
DrS0298=(åni×S0298i)продукты–(åni×S0298i)исх. вещества .
Пример. Определить изменение энтропии в стандартных условиях при протекании реакции: CH4 (газ) + CO2 (газ) = 2CO (газ) + 2H2 (газ)
| Вещество | CH4 (газ) | CO2 (газ) | CO (газ) | 2H2 (газ) |
| S0298, Дж/моль×К | 186,27 | 213,66 | 197,55 | 130,52 |
Решение.
DrS0298=(åni×S0298i)продукты–(åni×S0298i)исх. вещества,
DrS0298 = (2×197,55 + 2×130,52) – (1×186,27 + 1×213,66) = 256,21 [Дж/K].
Отметим, что второе начало термодинамики нельзя распространять на неограниченную (бесконечную) систему. В этом случае термодинамическая вероятность становится неопределенной (бесконечное число состояний). Допустимо рассматривать системы ограниченного масштаба. С другой стороны, нельзя распространять второе начало термодинамики на системы, состоящие из малого числа частиц. Вследствие своего вероятностного характера оно применимо только к системам, состоящим из статистически значимого (более 1012 ÷ 1014) числа частиц, и выполняется тем точнее, чем больше частиц в системе.
Дата добавления: 2017-02-20; просмотров: 659;
