Химический потенциал

Энергетические превращения, происходящие в системах при совершении процессов в различных условиях, описываются с использованием соответствующих термодинамических функций U, H, G, A. Необходимо отметить, что эти функции вводились для идеального процесса, в котором количество каждого вещества считалось неизменным и равным одному молю. Однако их величины должны зависеть от количества данного вещества в системе, которое может изменяться в ходе процесса. Например, в замкнутой системе при протекании химической реакции уменьшается количество исходных веществ и увеличивается количество продуктов при сохранении общей массы вещества (меняется качественный и количественный состав системы). Для учета влияния этого обстоятельства на величины термодинамических функций было введено понятие химического потенциала.

Приращение внутренней энергии системы при увеличении количества данного вещества в условиях постоянства энтропии системы и ее объема, при постоянстве количеств остальных веществ, получило название химический потенциал i-го вещества:

.

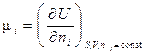Можно показать, что величина химического потенциала i-го вещества определяется изменением термодинамической функции при изменении количества данного вещества на один моль в процессах, протекающих при постоянстве соответствующих параметров и неизменном количестве остальных веществ:

.

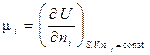
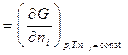
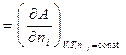
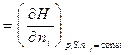В изобарно-изотермических процессах изменение энергии Гиббса при изменении количества i-го вещества будет определяться выражением dG =m_i×dn_i. При протекании химической реакции изменяются количества всех веществ, участвующих в реакции, поэтому dG =Sm_i×dn_i.

Условием равновесия химической реакции, происходящей в изобарно-изотермических условиях, D_rG =0, следовательно, Sm_i×dn_i = 0. Для реакции n_аA + n_bB = n_сC + n_dDусловием равновесия будет Sm_i×n_i = 0,

(m_c×n_C + m_d×n_D)–(m_a×n_A + m_b×n_B)=0.

Очевидно, что химический потенциал i-го вещества будет зависеть от его количества в единице объема – от концентрации вещества. Эту зависимость можно получить, рассмотрев изменение энергии Гиббса при изобарно-изотермическом смешивании двух идеальных газов.

Пусть два идеальных газа, находящихся в стандартных условиях, разделены перегородкой и занимают объемы V₁ и V₂ соответственно (рис.5.5).

Рис. 5‑5 Смешивание двух идеальных газов в изобарно-изотермических условиях в результате взаимной диффузии

Количество первого газа равно одному молю (n₁=1), а второго n₂. Если убрать перегородку, происходит смешивание газов в результате взаимной диффузии. Каждый газ займет весь объем системы, и объем каждого составит V₁ + V₂. При этом концентрация каждого газа (количество вещества в единице объема) уменьшится. Каждый газ совершит работу расширения при постоянном давлении и температуре. Очевидно, что в результате этого процесса энергия Гиббса системы уменьшится на величину совершенной работы расширения.

Изменение энергии Гиббса в результате уменьшения концентрации первого газа будет равно его работе расширения. Работа расширения первого газа определяется следующим образом:

dA = p⁰×dV,учитывая, что p×V =n×R×T и n₁=1,

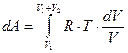® A =–R×T×ln .

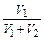Поскольку равные объемы идеальных газов содержат одинаковое число молей вещества,

,

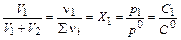где X₁ – мольная доля 1-го газа; p₁ – парциальное давление 1-го газа; р⁰ = 1,013×10⁵ Па – стандартное давление; С₁ – молярная концентрация 1-го газа; С⁰=1 моль/л стандартная концентрация.

Таким образом, энергия Гиббса 1-го газа изменится на величину DG₁=R×T×lnX₁. Поскольку n₁=1 моль, то, очевидно, D_fG_i =D_fG⁰_i + R×T×lnX_i.

Таким образом, химический потенциал вещества зависит от его концентрации в смеси:

m_i =m_i⁰ + R×T×lnX_i, m_i =m_i⁰ + R×T×ln 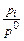, m_i =m_i⁰ + R×T×ln .

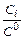Необходимо отметить, что данные концентрационные зависимости химического потенциала характеризуют идеальные газы и растворы. Межмолекулярные взаимодействия в реальных газах и растворах приводят к отклонению расчетных химических потенциалов от величин, полученных для идеальных систем. Для учета этого вводятся понятия фугитивности иактивности.

Фугитивность f (летучесть) – термодинамическая величина, служащая для описания свойств реальных газовых смесей. Она позволяет применять уравнения, выражающие зависимость химического потенциала идеального газа от температуры, давления и состава системы. При этом парциальное давление компонента газовой смеси p_i заменяется на его фугитивность f_i. Межмолекулярное взаимодействие приводит к уменьшению значения эффективного парциального давления компонента газовой смеси. Для учета этого величина парциального давления умножается на коэффициент фугитивности (g_i<1).Очевидно, что при p_i®0 g_i®1 и f_i ® p_i.

В отличие от идеальных, в реальных растворах имеются межмолекулярные взаимодействия и взаимодействия между ионами, образующимися в результате электролитической диссоциации. Это приводит к тому, что эффективная концентрация молекул и ионов в реальных растворах уменьшается. Поэтому при вычислении химического потенциала используют вместо концентрации С величину активности а. Активность и молярная концентрация i-го компонента связаны соотношением а_i =g_i×С_i, где g_i – молярный коэффициент активности (g_i<1). Очевидно, что при С_i®0 g_i®1 и а_i ® С_i.

Контрольные вопросы.

1. Термодинамическая система, параметры и функции состояния. Термодинамический процесс.

2. Первое начало термодинамики. Внутренняя энергия и энтальпия.

3. Тепловой эффект химической реакции. Энтальпия образования вещества.

4. Температурная зависимость энтальпии.

5. Энтропия. Второе начало термодинамики.

6. Направление протекания химического процесса.Энергия Гиббса.

7. Температурная зависимость величины энергии Гиббса.

8. Концентрационная зависимость энергии Гиббса. Активность и фугитивность.

9. Термодинамические расчеты теплового эффекта химической реакции.

10 Оценка термодинамической возможности протекания химической реакции.