Интегральная функция распределения

Интегральная функция распределения позволяет задать как дискретную, так и непрерывную случайную величину.

Интегральная функция распределения (ИФР) – это функция F(x), определяющая для каждого возможного значения x вероятность того, что случайная величина X примет значение меньшее x, т. е.

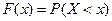
Геометрический смысл интегральной функции распределения – это вероятность того, что случайная величина X примет значение, которое на числовой оси лежит левее точки x.

Свойства интегральной функции распределения:

1. Значения интегральной функции распределения принадлежат отрезку

[0;1] : .

2. Вероятность того, что случайная величина X примет значение, заключенной в интервале (a,b), равна приращению интегральной функции распределения на этом интервале

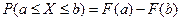
3. Если все возможные значения x случайной величины принадлежат интервалу (a, b), то

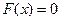, если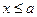

, если

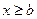
График ИФР непрерывной случайной величины представлен на рис. 2

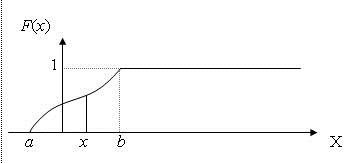
Рис. 2 График ИФР непрерывной случайной величины

График ИФР дискретной случайной величины представлен на рис. 3

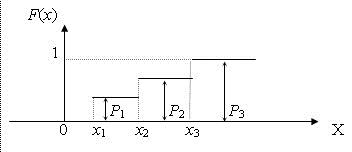
Рис. 3 График ИФР дискретной случайной величины