Разделение затрат на переменные и постоянные
Реальные затраты обычно являются полупеременными, поэтому в целях исследования поведения затрат с помощью линейной функции 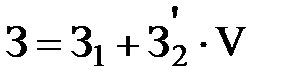 их нужно разделить на переменные и постоянные компоненты.
их нужно разделить на переменные и постоянные компоненты.
Существуют три основных метода дифференциации затрат:
1. метод максимальной и минимальной точки (мини-макси);
2. метод наименьших квадратов;
3. графический метод.
Пример. Выделить переменную и постоянную составляющие РСЭО при производстве продукта "А".
Исходные данные
| Месяц | Объем, шт. "А" | РСЭО, тыс. руб. |
| I | ||
| II | ||
| III | ||
| IV | ||
| V | ||
| VI | ||
| VII | ||
| VIII | ||
| IX | ||
| X | ||
| XI | ||
| XII | ||
| Итого | ||
| Среднее за год | 20,5 (246 : 12) | 500,75 (6009 : 12) |
Метод мини-макси состоит в следующем:
– выбираются два периода: с наибольшим и наименьшим объемом (V) производства (max=24; min=17);
– определяется разница в объемах производства и в затратах на эти объемы и предполагается, что постоянная часть расходов не изменяется, а изменения в затратах вызваны только изменением переменных издержек
Dзатрат = 507 – 493 = 14,
Dобъемов = 24 – 17 = 7;
– рассчитывается ставка (величина) переменных затрат на 1 единицу объема
| Переменные расходы на единицу продукции | 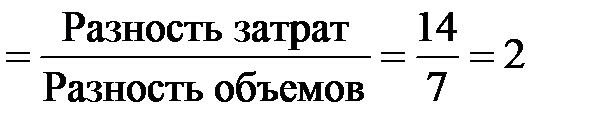 тыс. руб.; тыс. руб.;
| или |
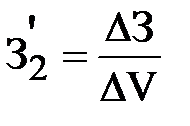 ,
,
– тогда постоянные расходы можно найти двумя способами: через min и max точки.
Постоянные расходы = Общие – переменные =
= Общие – переменные на 1 ед. ´ кол-во единиц;
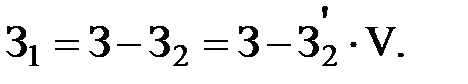
Постоянные расходы = 507(max) – 2 ´ 24 = 459 или 493(min) – 17 ´ × 2 = 459, т.е. расчеты совпадают.
Сведем решение в таблицу.
| Показатели | Объем производства, шт. | Затраты, тыс. руб. |
| 1. Max точка (высшая) | ||
| Min точка (низшая) | ||
| 2. Разности в уровнях | 24 – 17 = 7 | 507 – 493 = 14 |
| 3. Переменные затраты в единице продукции | 14 : 7 = 2 | |
| 4. Постоянные затраты: | ||
| для max точки | 507 – (24 ´ 2) = 459 | |
| для min точки | 493 – (17 ´ 2) = 459 | |
| 4. Общее уравнение: Все затраты (совокупные) | З = 459 + 2 ´ V |
Метод будет корректным, если расходы по данному фактору взяты только в области релевантности. В частности, если минимальный объем вызван случайными причинами (отсутствие сырья, поломка и т.д.), то картина будет искажена.
Более точным является "метод наименьших квадратов". Его суть – сумма квадратов отклонений фактических значений функции от значений, найденных по уравнению регрессии, должна быть наименьшей. Уравнение применяем к среднегодовому значению:
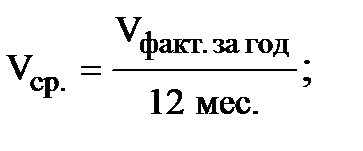
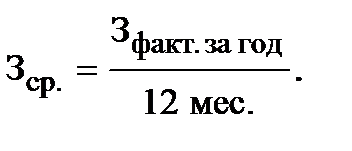
В нашем случае уравнение регрессии:
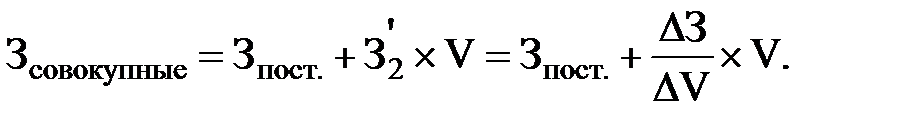
Отклонение по объему за месяц определится разностью фактических затрат и среднегодовым их уровнем за месяц:
DV = Vфакт. – Vср.
Отклонение по объему за год:
SDV = S(Vфакт. – Vср.) = 0.
Аналогично отклонение по затратам за месяц:
DЗ = Зфакт. – Зср..
Отклонение по затратам за год:
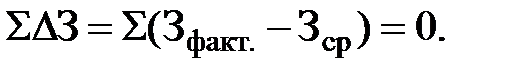
Чтобы избавиться от знаменателя, равного нулю, в уравнении 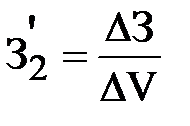 за год, берут квадрат отклонений объемов производства, тогда
за год, берут квадрат отклонений объемов производства, тогда
З2' 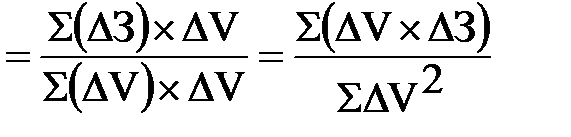 .
.
Расчеты за январь представим в таблице.
| № п/п | Показатели | Методика расчета | Расчет | Значение |
| 1. | Выпуск, шт (V) | Задан в условии | - | |
| 2. | Разность между фактическим и среднегодовым выпуском, DV | Vянв. – Vср.год. | 20 – 20,5 | -0,5 |
| 3. | Совокупные затраты, З | Заданы в условии | - | 500,0 |
| 4. | Разность между фактическими и среднегодовыми совокупными затратами, DЗ | Зянв. – Зср.год. | 500 – 500,75 | -0,75 |
| 5. | Квадрат разности пункта 2, DV2 | (Vянв. – Vср.год.)2 | (-0,5)2 | +0,25 |
| 6. | Расчетная величина | DV´ [RIO1] DЗ | -0,5´(-0,75) | +0,375 |
Аналогичный расчет следует сделать за все месяцы. Данные сведем в таблицу.
| Месяц | Объем, шт. | Отклонение по объему | Затраты, тыс. руб. | Отклоне-ние по затратам, тыс. руб. | Квадрат от-клонений по объему | Расчетная величина |
| Обозна-чение | V | DV | З | DЗ | DV2 | DV´ [RIO2] DЗ |
| I | -0,5 | -0,75 | +0,25 | 0,375 | ||
| II | 1,5 | +11,25 | +2,25 | 16,875 | ||
| III | 0,5 | +5,25 | +0,25 | 2,625 | ||
| IV | -0,5 | -10,75 | +0,25 | 5,375 | ||
| V | -1,5 | -8,75 | +2,25 | 13,125 | ||
| VI | -1,5 | -5,75 | +2,25 | 8,625 | ||
| VII | -2,5 | -3,75 | +6,25 | 9,375 | ||
| VIII | -3,5 | -7,75 | +12,25 | 27,125 | ||
| IX | +0,5 | +4,25 | +0,25 | 2,125 | ||
| X | +3,5 | +6,25 | +12,25 | 21,875 | ||
| XI | +2,5 | +4,25 | +6,25 | 10,625 | ||
| XII | +1,5 | +6,25 | +2,25 | 9,375 | ||
| Итого | 47,0 | 127,5 | ||||
| Среднее за год | 20,5 | 500,75 |
Теперь можно рассчитать переменные и постоянные части расходов в единице продукции.
| № п/п | Показатели | Методика расчета | Расчет | Значение |
| 1. | Переменные расходы в единице продукции, З'2 |
З'2= 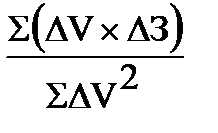
| 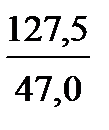
| 2,713 |
| 2. | Переменные затраты на среднегодовой выпуск, З2 | З2 =З'2 ´ Vср. | 2,713 ´ 20,5 | 55,62 |
| 3. | Постоянные затраты | З1 = Зср. – З2 | 500,75 – 55,62 | 445,13 |
Тогда общее уравнение регрессии для нашего примера:
З = 445,13 + 2,713 ´ V.
Способ "макси-мини" давал уравнение З = 459 + 2 × V. Расчет методом "наименьших квадратов" более точен, но гораздо сложнее, однако по нему имеются компьютерные программы .
Графический метод – на основе данных изменений объемов производства и изменений величины общих затрат находят точки затрат, затем приблизительно чертят прямую, наиболее близкую к точкам. Точка пересечения этой линии с осью затрат определяет величину постоянных затрат.
Дата добавления: 2018-09-24; просмотров: 4801;
