Вопрос 1 Обоснование задачи исследования согласованных изменений

МЕТОД РАНГОВОЙ КОРРЕЛЯЦИИ

Первоначальное значение термина "корреляции" - взаимная связь (Oxford Advanced Learner's Dictionary of Current English, 1982). Когда говорят о корреляции, используют термины "корреляционная связь" и"корреляционная зависимость".

Корреляционная связь - это согласованные изменения двух при­знаков или большего количества признаков (множественная корреляци­онная связь). Корреляционная связь отражает тот факт, что изменчи­вость одного признака находится в некотором соответствии с изменчи­востью другого (Плохинский Н.А., 1970, с. 40). "Стохастическая¹ связь имеется тогда, когда каждому из значений одной случайной вели­чины соответствует специфическое (условное) распределение вероятно­стей значений другой величины, и наоборот, каждому из значений этой другой величины соответствует специфическое (условное) распределение вероятностей значений первой случайной величины" (Суходольский Г.В., 1972, с. 178).

^1.Стохастическая означает вероятностная. Связи между случайными явлениями называют вероятностными ,или стохастическими связями (Суходольскнй Г. В., 1972, с. 52). Этот термин подчеркивает их отличие от детерминированных или функциональных связей а физике или математике (связь площади треугольника с его высотой и основанием, связь длины окружности с ее радиусом и т. п.). В функциональных связях каждому значению первого признака всегда соответствует (в идеальных условиях) совершенно определенное значение другого признака (Плохинский Н.А., 1970, с. 41). В корреляционных связях каждому значению одного признака может соответствовать определенное распределение значений другого признака, но не определенное его значение.

Корреляционная зависимость - это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака.

Оба термина - корреляционная связь и корреляционная зависи­мость - часто используются как синонимы (Плохинский Н.А.,1970; Суходольский Г.В.,1972; Артемьева Е.Ю., Мартынов Е.М.,1975 и др.). Между тем, согласованные изменения признаков и отражающая это корреляционная связь между ними может свидетельствовать не о зави­симости этих признаков между собой, а зависимости обоих этих при­знаков от какого-то третьего признака или сочетания признаков, не рассматриваемых в исследовании.

Зависимость подразумевает влияние, связь - любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной связи, они свидетельствуют лишь о том, что изменениям одного при­знака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков или она оказы­вается за пределами исследуемой пары признаков, нам неизвестно.

Говорить в строгом смысле о зависимости мы можем только в тех случаях, когда сами оказываем какое-то контролируемое воздействие на испытуемых или так организуем исследование, что оказывается возмож­ным точно определить интенсивность не зависящих от нас воздействий. Воздействия, которые мы можем качественно определить или даже из­мерить, могут рассматриваться как независимые переменные. Признаки, которые мы измеряем и которые, по нашему предположению, могут из­меняться под влиянием независимых переменных, считаются зависимы­ми переменными. Согласованные изменения независимой и зависимой переменной действительно могут рассматриваться как зависимость.

Однако, учитывая, что число градаций, или уровней, зависимой переменной обычно невелико, целесообразнее применять в такого рода исследованиях не корреляционный метод, а методы выявления тенден­ций изменения признака при изменении условий, например, критерии тенденций Н Крускала-Уоллиса и L Пейджа (см. Главы 2 и 3) или метод дисперсионного анализа (см. Темы 8 и 9).

Если в исследование включены независимые переменные, кото­рые мы можем по крайней мере учитывать, например, возраст, то мож­но считать выявляемые между возрастом и психологическими признаками корреляционные связи корреляционными зависимостями. В боль­шинстве же случаев нам трудно определить, что в рассматриваемой па­ре признаков является независимой, а что - зависимой переменной.

Учитывая, что термин "зависимость" явно или неявно подразуме­вает влияние, лучше пользоваться более нейтральным термином "корреляционная связь".

Корреляционные связи различаются по форме, направлению и степени (силе).

По формекорреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решае­мых задач в контрольной сессии. Криволинейной может быть, напри­мер, связь между уровнем мотивации и эффективностью выполнения задачи (см. Рис. 6.1). При повышении мотивации эффективность вы­полнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффектив­ность выполнения задачи; дальнейшему повышению мотивации сопутст­вует уже снижение эффективности.

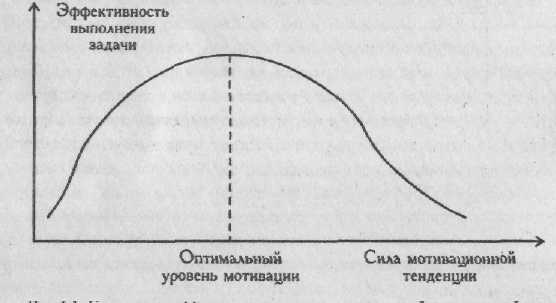
Рис. 6.1. Связь между эффективностью решения задачи и силой мотивационной тен­денции (по j.W. Atkinson. I974. р.200)

По направлениюкорреляционная связь может быть положитель­ной ("прямой") и отрицательной ("обратной").

При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значе­ниям одного признака - низкие значения другого (см. Рис. 6.2).

При отрицательной корреляции соотношения обратные.

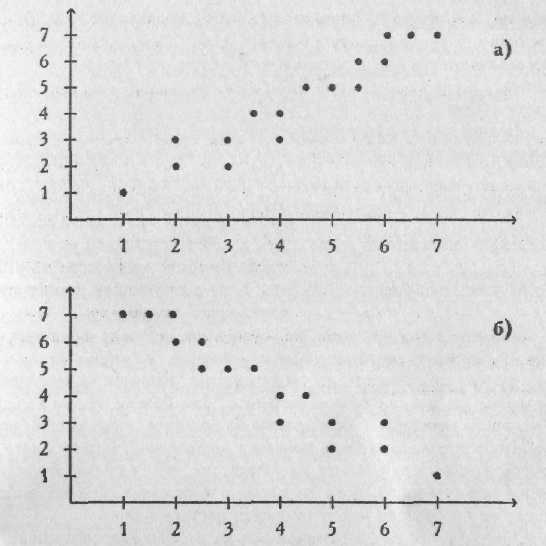
Рис. 6.2. Схема прямолинейных корреляционных связей;

А - положительная (прямая) корреляционная связь;

В- отрицательная (обратная) корреляционная связь

*При положительной корреляции коэффициент корреляции имеет положительный знак, например r=+0,207,

*при отрицательной корреля­ции - отрицательный знак, например r= - 0,207.

Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции.

Силасвязи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Максимальное воз­можное абсолютное значение коэффициента корреляции r=1,00; мини­мальное r=0.

Используется две системы классификации корреляционных связей по их силе: общая и частная.

Общая классификация корреляционных связей (по Ивантер Э.В., Коросову А.В., 1992):

1)сильная, или тесная при коэффициенте корреляции r >0,70;

2)средняя при 0,50< r <0,69;

3)умеренная при 0,30< r <0,49;

4)слабая при 0,20< r <0,29;

5)очень слабая при r <0,19.

Частная классификация корреляционных связей:

1) высокая значимая корреляция - при г, соответствующем уровню статистической значимости р<0,01;

2)значимая корреляция - при r, соответствующем уровню

статистической значимости р<0,05;

3) тенденция достоверной связи при г, соответствующем уровню статистической значимости р<0,10;

4)незначимая корреляция - при r , не достигающем уровня статистической значимости.

Две эти классификации не совпадают.

*Первая ориентирована только на величину коэффициента корреляции, а

*вторая определяет, какого уровня значимости достигает данная величина коэффициента корреляции при данном объеме выборки. Чем больше объем выборки, тем меньшей величины коэффициента корреляции оказывается доста­точно, чтобы корреляция была признана достоверной. В результате при малом объеме выборки может оказаться так, что сильная корреляция окажется недостоверной. В то же время при больших объемах выборки даже слабая корреляция может оказаться достоверной.

Обычно принято ориентироваться на вторую классификацию, по­скольку она учитывает объем выборки. Вместе с тем, необходимо пом­нить, что сильная, или высокая, корреляция - это корреляция с коэффи­циентом r>0,70, а не просто корреляция высокого уровня значимости.

В качестве мер корреляции используются:

1) эмпирические меры тесноты связи, многие из которых были получе­ны еще до открытия метода корреляции, а именно:

а) коэффициент ассоциации, или тетрахорический показатель связи;

б) коэффициенты взаимной сопряженности Пирсона и Чупрова;

в) коэффициент Фехнера;

г) коэффициент корреляции рангов;

2)линейный коэффициент корреляции r;

3)корреляционное отношение ή

4)множественные коэффициенты корреляции и др.

Подробное описание этих мер можно найти в руководствах Венецкого И.Г., Кильдишева Г.С.(1968), Плохинского Н.А.(1970), Суходольского f.B.(1972), Ивантер Э.В., Коросова А.В.(1992) и др.

В психологических исследованиях чаще всего применяется коэф­фициент линейной корреляции r Пирсона. Однако этот метод является параметрическим и поэтому не лишен недостатков, свойственных пара­метрическим методам. Параметрическими являются также методы определения корреляционного отношения и подсчета множественных коэффициентов корреляции. Кроме того, эти методы, как правило, требуют машинной обработки данных. По этим причинам они остаются за пределами нашего рассмотрения.

Все эмпирические меры тесноты связи, кроме коэффициента ранговой корреляции, могут быть заменены методами сопоставления и сравнения, изложенными ранее.

Ведь что, в сущности, мы доказываем, когда обосновываем разли­чия в долях двух выборок, характеризующихся исследуемым эффектом? Мы показываем, что если испытуемый относится к одной из выборок, то, скорее всего, он будет характеризоваться какими-то определенными значениями исследуемого признака, а если он относится к другой из двух выборок, то он будет характеризоваться (с большой степенью вероятности) другими значениями исследуемого признака. Фактически мы исследуем сопряженные изменения двух признаков: отнесенность к той или иной выборке и определенные значения исследуемого признака.

Что мы доказываем, с другой стороны, когда два распределения признака оказываются сходными или, наоборот, статистически досто­верно различающимися между собой? Мы доказываем, что в обеих выборках частоты встречаемости разных значении признака распределяют­ся согласованно или, наоборот, несогласованно.

Мы, правда, скорее определяем меру рассогласованности, чем согласованности, но все же часто метод χ² относится к числу методов, выявляющих степень согласованности или даже связи.

Методы выявления тенденций уже напрямую заменяют меры эмпирической сопряженности, позволяя нам проследить возрастание значений признака при изменении условий. Фактически мы отвечаем на вопрос о том, согласованно ли изменяются условия и значения иссле­дуемого признака.

Быть может, современному психологу не очень просто отказаться от метода подсчета корреляций. Это очень привычно - подсчитывать корреляции. Исторически сложилось так, что этот метод является одним из основных методов статистической обработки. Главное преимущество кор­реляционного анализа состоит в том, что можно сразу провести множе­ственное сопоставление признаков.

Например, нам необходимо опреде­лить, с чем связана успешность в какой-либо деятельности. Исследова­тель может предполагать, что она связана с уровнем интеллектуального развития, с некоторыми из личностных факторов 16-факторного опрос­ника Кеттелла, а может быть, с уровнем эмпатии, тревожности или фрустрационной толерантности, с возрастом самого испытуемого или воз­растом матери в момент его рождения и т.д. и т.п. В итоге он получает связи, отражающие среднегрупповые тенденции сопряженного измене­ния признаков. Но дело как раз в том, что у каждого отдельного испы­туемого успешность в данном виде деятельности может определяться разными психологическими характеристиками или разными их сочета­ниями. Метод корреляций отдает предпочтение группе, а не отдельному индивиду.

Против этого можно возразить, что и все остальные статистиче­ские методы отдают предпочтение среднегрупповым, а не индивидуаль­ным тенденциям. Однако это не совсем так. Например, метод тенден­ций L Пейджа определяет степень согласованности индивидуальных тенденций, критерий χ²_r, Фридмана—степень совпадения или несовпаде­ния индивидуальных соотношений рангов, биномиальный критерий m -степень отклонения индивидуальных значений от заданных или средне­статистических и т.п.

Прежде чем переходить к корреляциям, исследователю необходимо проанализировать полученные данные с помощью критериев сравнения и сопоставления еще и по другой причине. Возможно, размах вариатив­ности признака в обследованной выборке окажется слишком узким, чтобы можно было распространять полученную корреляцию на весь возможный диапазон его значений. Например, может оказаться так, что в обследованной группе по какому-либо из факторов 16-факторного личностного опросника Кеттелла получены лишь низкие и средние зна­чения, и в то же время выявлена значимая положительная связь этого личностного фактора с успешностью профессиональной деятельности. Не учитывая истинного размаха значений в данной выборке, можно экстраполировать полученную связь и на высокие значения фактора, что может оказаться ошибкой.

Во-первых, связь данного фактора с ус­пешностью деятельности может на самом деле быть криволинейной, как в рассмотренном выше случае связи уровня мотивации с эффективно­стью выполнения задания (см. Рис. 6.1).

Во-вторых, не исключено, что самым важным результатом исследования является как раз факт низких и средних значений данного личностного фактора в обследованной вы­борке, а исследователь не обратил на него внимания, привычно отдав предпочтение корреляционной матрице, а не таблице первичных данных.

Математическая обработка должна начинаться с использования "самых простых приемов с совершенно понятной для исследователя сутью производимых преобразований" (Дворяшнна М.Д., Пехлецкий И.Д., 1976, с. 45). Учитывая большие возможности методов первичной обра­ботки данных, изложенных в Темах 3-6, не исключено, что этими приемами математическая обработка может и заканчиваться. Эти мето­ды дают и основание для достоверных выводов, и материал для вы­движения новых гипотез, и стимул к новым размышлениям.

И все же, если исследователь хочет применить метод корреляций, в настоящем пособии предлагается использовать коэффициент ранговой корреляции Спирмена.

Основанием для выбора этого коэффициента служат:

а) его универсальность;

б) простота;

в) широкие возможности в решении задач сравнения индивидуаль­ных или групповых иерархий признаков.

Универсальность коэффициентаранговой корреляции проявляется в том, что он применим к любым количественно измеренным или ран­жированным данным. Простота метода позволяет подсчитывать корре­ляцию "вручную". Уникальность метода ранговой корреляции состоит в том, что он позволяет сопоставлять не индивидуальные показатели, а индивидуальные иерархии, или профили, что недоступно ни одному из других статистических методов, включая метод линейной корреляции (Плохинский Н.А., 1970, с. 167).

Коэффициент ранговой корреляции рекомендуется применять в тех случаях, когда нам необходимо проверить, согласованно ли изменя­ются разные признаки у одного и того же испытуемого и насколько совпадают индивидуальные ранговые показатели у двух отдельных ис­пытуемых или у испытуемого и группы.

Вопрос 2