Тестирование выходных параметров РЭУ методом Монте-Карло
Метод статистических испытаний (Монте- Карло) относится к вероятностному моделированию с использованием математических моделей РЭУ. Предположим, что модель задана математическим выражением в виде функции
| y=j(x1, ¼xn, t) | (1) | |
| где | у - выходной параметр; | |
| x1, ¼xn -- первичные параметры; | ||
| t – время (в общем случае может также рассматриваться как первичный параметр). | ||
Обычно требуется определить закон распределения выходного параметра у в различные моменты времени t, если известны пределы изменения первичных параметров x1, ¼xn
Зафиксируем время t = t0. Взяв по одному случайному значению для каждого из п первичных параметров, получим их случайную комбинацию
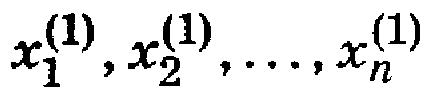
где верхний индекс означает ее номер. Подставив эту комбинацию в математическую модель вида (1), найдем первое значение выходного параметра y(1).
Повторив процедуру получения случайных комбинаций первичных параметров и подставив их в выражение (1) N раз, получим ряд
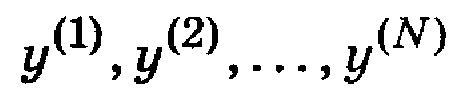
Он содержит информацию о среднем значении выходного параметра у, степени его рассеивания относительно среднего значения, а также о законе распределения для момента времени t = t0 . Эта процедура повторяется для других фиксированных, моментов времени с выбранным шагом Dt.
Статистическая обработка результатов моделирования в данном случае состоит в определении для каждого момента времени среднего значения и среднего квадратического отклонения выходного параметра, а также в построении для него гистограммы распределения и подборе подходящей модели закона распределения.
Вследствие большого объемаобъёма обрабатываемых данных метод Монте-Карло реализуется с помощью ЭВМ. укрупненнаяУкрупнённая структурная схема алгоритма решения рассмотренной задачи на ЭВМ приведена на рис. Она соответствует предположению, что первичные параметры являются некоррелированными и подчиняются нормальному закону или закону равной вероятности.
Алгоритм решения задачи на ЭВМ методом Монте-Карло содержит следующие основные блоки (многие из них повторяются в алгоритме испытаний по методу Монте-Карло неоднократно):
 Ввод исходных данных: mi, si, и ki -- среднее значение, среднее квадратическое отклонение первичного параметра и код закона его распределения, например, (0 - нормальный закон, 1 - закон равной вероятности), начальный и конечный моменты времени, для которых определяют значения выходного параметра, выбранный шаг изменения фиксированных моментов времени, количество первичных параметров n, количество реализаций выходного параметра N.
Ввод исходных данных: mi, si, и ki -- среднее значение, среднее квадратическое отклонение первичного параметра и код закона его распределения, например, (0 - нормальный закон, 1 - закон равной вероятности), начальный и конечный моменты времени, для которых определяют значения выходного параметра, выбранный шаг изменения фиксированных моментов времени, количество первичных параметров n, количество реализаций выходного параметра N.
 Организация цикла по индексу i. Индексом учитываются первичные параметры хi, i= 1,...n.
Организация цикла по индексу i. Индексом учитываются первичные параметры хi, i= 1,...n.
 Организация цикла по индексу j. Индексом учитываются реализации выходного параметра y.
Организация цикла по индексу j. Индексом учитываются реализации выходного параметра y.
 Обращение к датчику нормально распределенныхраспределённых случайных чисел и формирование случайного числа хi
Обращение к датчику нормально распределенныхраспределённых случайных чисел и формирование случайного числа хi
 Обращение к датчику равномерно распределенныхраспределённых случайных чисел и формирование случайного числа хi
Обращение к датчику равномерно распределенныхраспределённых случайных чисел и формирование случайного числа хi
 Статистическая обработка результатов моделирования выходного параметра при фиксированном значении t
Статистическая обработка результатов моделирования выходного параметра при фиксированном значении t
Можно заметить, что ряд процедур подобны используемым в экспериментальном методе определения коэффициентов влияния параметров элементов, но там процедура более проста и не оперирует со случайными величинами.
Достоинство метода Монте-Карло состоит в том, что он даетдаёт возможность оперировать законами распределения первичных и выходного параметров. Это позволяет получить результаты, обладающие большей достоверностью по сравнению с методами, которые оперируют числовыми характеристиками параметров - – средними значениями и средними квадратическими отклонениями.
Алгоритм испытаний методом Монте-Карло

Дата добавления: 2017-02-20; просмотров: 785;
