Применим метод сечения.

1) Пересечем гиперболический параболоид координатными плоскостями.

Найдем линию пересечения с плоскостью 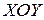. На этой плоскости 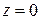, поэтому 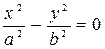. Это уравнение определяет на плоскости 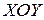пару пересекающихся прямых: .

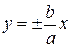Найдем линию пересечения с плоскостью 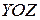. На этой плоскости 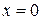, поэтому 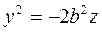. Это уравнение на плоскости 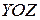задает параболу, ветви которой направлены вниз.

Сечение плоскостью 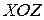также является параболой 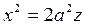, но ее ветви направлены вверх.

Сечения гиперболического параболоида координатными плоскостями

2) Рассмотрим сечение гиперболического параболоида плоскостями, параллельными координатным плоскостям.

2.1) Плоскостью .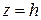

Уравнения этих линий .

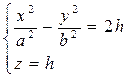При h > 0, в сечении получим гиперболу: 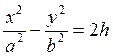с действительной осью OX.

При h = 0, 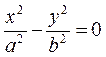, в сечении получим пару пересекающихся прямых: .

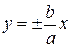При h < 0, в сечении получим гиперболу: 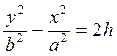с действительной осью OY.

2.2) Плоскостью .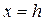

Уравнения этих линий .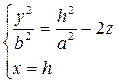

При любом h в сечении получим параболу .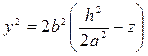

2.3) Плоскостью 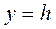. Аналогично п. 2.2.

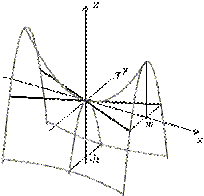
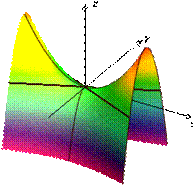
Изображение гиперболического

параболоида с помощью сечений Гиперболический параболоид