Применим метод сечения.

1) Пересечем эллипсоид координатными плоскостями.

Найдем линию пересечения эллипсоида с плоскостью 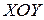, при этом 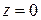, и координаты точек эллипсоида на плоскости 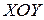удовлетворяют уравнению 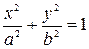. Следовательно, линия пересечения является эллипсом с полуосями 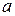и .

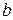Сечение плоскостью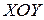

Аналогично,

сечение в плоскости 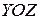дает эллипс 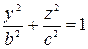, с полуосям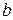и и ;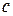

сечение плоскостью 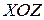- эллипс 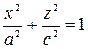с полуосям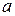и и .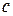

Сечения эллипсоида координатными плоскостями

2) Рассмотрим сечение эллипсоида плоскостями, параллельными координатным плоскостям.

2.1) Плоскостью .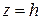

Эта плоскость параллельна плоскости 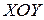и пересекает ось 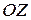в точке .

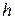Уравнения этой линии .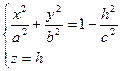

а) если 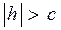, то 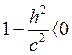, получили в левой части первого уравнения неотрицательное число, а в правой – отрицательное, следовательно, уравнение решений не имеет, и точек пересечения нет.

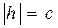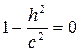b) если , то и 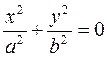, следовательно в сечении получим точк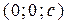и или 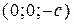в зависимости от знака .

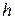с) если 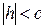, то .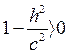

Тогда первое уравнение преобразуем к виду 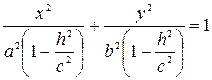, то есть к виду: 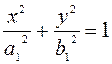, где , .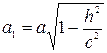

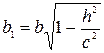Полученное уравнение является уравнением эллипса.

Сечение плоскостью 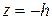является таким же эллипсом, расположенным симметрично первому относительно плоскости .

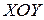2.2) Плоскостью 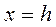. Аналогично п. 2.1.

2.3) Плоскостью 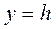. Аналогично п. 2.1.

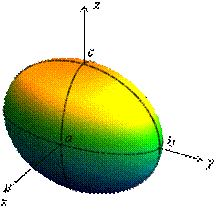
Дополнительные сечения эллипсоида Эллипсоид

Если в уравнении (1) две полуоси равны друг другу, например, а = b, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей (например, ОZ).

Его уравнение примет вид: .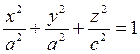

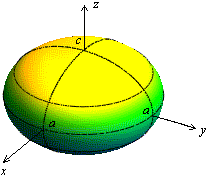
Эллипсоид вращения

ГИПЕРБОЛОИДЫ

План: 1. Однополостный гиперболоид.

2. Двуполостный гиперболоид.

Вопрос.

Определение 1. Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольно декартовой системе координат определяется каноническим уравнением: 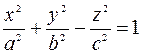, (1).

Исследуем уравнение (1) и определим форму однополостного гиперболоида.

1. Точка О (0;0;0) не принадлежит однополостному гиперболоиду, так как ее координаты не удовлетворяют уравнению (1).

2. Переменные x, y, z входят в уравнение в четной степени, следовательно, если точка М(x, y, z) принадлежит поверхности, то ей будет принадлежать 7 точек: М₁ (-x, y, z); М₂ (x, - y, z); М₃ (x, y, - z); М₄ (- x, - y, z);

М₅ (- x, y, - z); М₆ (x, - y, - z); М₇ (- x, - y, - z).

Таким образом, однополостный гиперболоид фигура симметричная относительно всех координатных осей, координатных плоскостей, начала координат.

3. Найдем точки пересечения однополостного гиперболоида с осями координат:

С осью ОХ: y = z = 0. Из уравнения (1) следует, х² = а² , отсюда х = ± а.

А₁(а; 0; 0), А₂(-а; 0; 0).

С осью ОУ: x = z = 0. Из уравнения (1) следует, у² = b² , отсюда y = ± b.

В₁(0; ,b; 0), В₂(0; -b; 0).

С осью ОZ: y = х = 0. Из уравнения (1) следует, z ² = - с² , следовательно однополостный гиперболоид не пересекает ось ОZ. Ось ОZ – мнимая ось.