Расчет аппаратов для фильтрования

Уравнения фильтрования. В первом приближении движение жидкости через слой осадка и фильтровальную перегородку можно рассмотреть как движение через слой зернистого материала. Тогда с учетом (5.231), (5.235), (5.241)

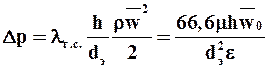. (9.19)

Общий перепад давлений складывается из перепада давлений на слое осадка и фильтровальной перегородки:

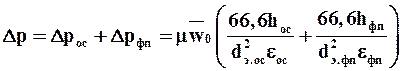, (9.19а)

откуда можно получить значение для :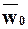

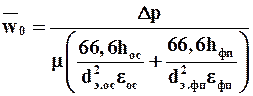. (9.19б)

Величина 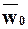является фиктивной скоростью движения чистой жидкости через слой зернистого (пористого) материала. Такое движение жидкости называется фильтрацией. При фильтровании, в общем случае, значения разности давлений и гидравлического сопротивления слоя осадка с течением времени изменяются, определение величин эквивалентных диаметров осадка (d_э,ос) и порозности осадка (e_ос) вызывает затруднение. Поэтому переменную скорость фильтрования выражают в дифференциальной форме:

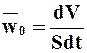(9.19в)

и дифференциальное уравнение фильтрования записывается в виде

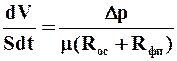, (9.20)

где V – объем фильтрата, м3; S – поверхность фильтрования, м2;t – продолжительность фильтрования, с; 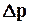- разность давлений, Па; m- коэффициент динамической вязкости жидкой фазы суспензии, Па 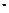с; – с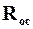опротивление слоя осадка, м^-1;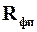- сопротивление фильтровальной перегородки, м^-1.

Для интегрирования уравнения (9.20) необходимо установить зависимость между сопротивлением слоя осадка и объемом полученного фильтрата. Учитывая пропорциональность объема осадка и фильтрата, обозначим x₀ отношение объема осадка к объему фильтрата. Тогда объем осадка будет равен x₀V. Объем осадка может быть выражен произведением 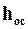S, где 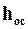– высота слоя осадка (м), следовательно,

,

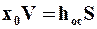откуда высота равномерного слоя осадка на фильтровальной перегородке составит

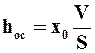. (9.21)

Сопротивление слоя осадка можно выразить равенством

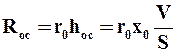, (9.22)

где r₀ – удельное объемное сопротивление слоя осадка, м-2.

Подставив 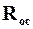из равенства (9.22) в уравнение (9.20), получаем

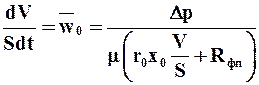. (9.23)

Допускаем, что сопротивлением фильтровальной перегородки можно пренебречь ( 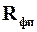= 0), тогда с учетом равенства (9.21) из уравнения (9.23) находим

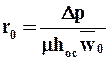. (9.24)

Таким образом удельное сопротивление осадка численно равно разности давлений, необходимой для того, чтобы жидкость с вязкостью 1 Па×с фильтровалась со скоростью 1 м/с сквозь осадок высотой 1 м.

ПринявV = 0, что соответствует началу фильтрования, когда на фильтровальной перегородке еще не образовался осадок, из уравнения (9.23) получаем

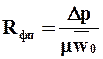. (9.24а)

Уравнение фильтрования при постоянной разности давлений. При Dр = const и неизменной температуре для фильтра данной конструкции и известной фильтровальной перегородки все входящие в уравнение (9.23) величины, за исключением V и t, постоянны. Интегрируем это уравнение в пределах от 0 до Vи от 0 до t:

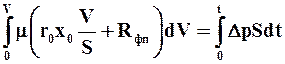(9.25)

или

.

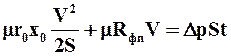Разделив обе части последнего уравнения на 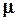r₀x₀/2S, получим

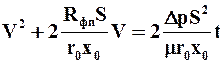. (9.26)

Уравнение (9.26) применимо к несжимаемым и сжимаемым осадкам, поскольку при Dр = const величины r₀ и x₀ тоже постоянны. Из уравнения (9.23) следует, что при Dр = const по мере увеличения объема фильтрата, а следовательно, и продолжительности фильтрования скорость фильтрования уменьшается.

Уравнения фильтрования при постоянной скорости процесса. При постоянной скорости фильтрования производную dV/dt можно заменить отношением конечных величин V/t. После такой замены, решая уравнение (9.23) относительно Dр, находим

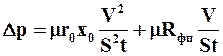. (9.27)

Умножив и разделив первое слагаемое правой части этого уравнения наt и приняв во внимание, что постоянная скорость фильтрования

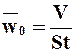, 9.28)

получаем

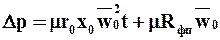. (9.29)

Уравнение (9.29) показывает, что при 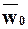= const разность давлений возрастает по мере увеличения продолжительности фильтрования.

Это уравнение применимо к несжимаемым осадкам; при использовании его для сжимаемых осадков следует иметь в виду зависимость удельного сопротивления осадка от разности давлений.

Уравнение фильтрования при постоянных разности давлений и скорости. Такой вид фильтрования осуществим, когда чистая жидкость движется сквозь слой осадка неизменной толщины при постоянной разности давлений. Движение чистой жидкости в пористой среде называется фильтрацией. Промывку осадка на фильтре способом вытеснения, когда над осадком имеется слой промывной жидкости, можно рассматривать как фильтрацию промывной жидкости сквозь слой осадка постоянной толщины при постоянных разности давлений и скорости.

Приняв в уравнении (9.23) в соответствии с равенством (9.21) вместо x₀V/S эквивалентную этому выражению толщину слоя осадка на перегородке 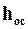и заменив dV/dt на значение V/t, при Dр = const получаем

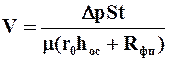. (9.30)

Поскольку Dр = const уравнение (9.30) применимо для несжимаемых и сжимаемых осадков.

Определение постоянных в уравнениях фильтрования. Под постоянными в уравнениях (9.26), (9.28) и (9.30) понимают r₀ , x₀и 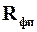. Для осадков, получаемых в химических производствах и состоящих, как правило, из частиц размером менее 100 мкм, эти величины находят экспериментально. Рассмотрим один из способов определения опытным путем указанных величин в уравнении фильтрования при Dр = const (9.26), характеризующийся большой точностью получаемых результатов.

Преобразуем уравнение (9.26) к виду

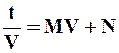, (9.31)

где 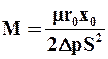, (9.32)

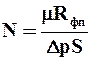. (9.33)

При постоянных температуре и разности давлений все величины, входящие в правые части равенств (9.32) и (9.33), постоянны. Поэтому значения M и N также постоянны, и уравнение (9.31) является уравнением прямой линии, наклоненной к оси абсцисс под углом, тангенс которого М, и отсекающей на оси ординат отрезок N. Для построения указанной прямой в координатах V – t/V наносят ряд точек на основании измеренных в опыте и соответствующих одно другому значений V и t/V (рис. 9.20).

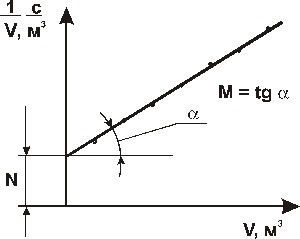
Рис. 9.20. К определению M и N в уравнении фильтрования

Затем по графику определяют величины M и N, после чего из равенств (9.32) и (9.33) вычисляют r₀ и 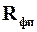. Величину x₀ находят в результате непосредственного измерения объемов осадка и фильтрата.

Для несжимаемых осадков, размер частиц которых достаточно велик (порядка 1мм и более), процесс фильтрования можно рассматривать как течение жидкости через зернистый слой. В этом случае величину r₀ с учетом уравнений (9.19а) и (9.24) можно определить по зависимости

.

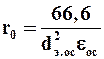Центробежное фильтрование. Для периодически действующей фильтрующей центрифуги можно выделить три периода: образование осадка, уплотнение осадка и его механическая сушка (отжим). В течение первого периода на поверхности фильтровальной перегородки образуется слой осадка, состоящий из твердых дисперсных частиц, толщина слоя увеличивается до тех пор, пока все элементы дисперсной фазы не перейдут из суспензии в осадок и внутренний радиус слоя суспензии R_c не сравняется с внутренним радиусом осадка R_о. В ходе второго периода происходит уплотнение осадка путем выдавливания жидкости. Третий период характеризуется замещением жидкости в порах осадка газовой фазой, что позволяет получать в процессе центробежного фильтрования менее влажные осадки, чем в осадительных центрифугах.

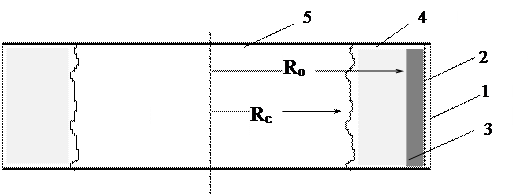Рис. 9.21. Схема барабана фильтрующей центрифуги:
1 – перфорированная стенка; 2 – фильтровальная перегородка; 3 – осадок; 4 – суспензия; 5 – газовая фаза

Движущей силой в первом периоде фильтрования является в основном разность давлений на внутренней поверхности осадка и на внешней поверхности фильтровальной перегородки. Пренебрегаем влиянием сил тяжести при больших значениях фактора разделения K_p (9.9) в центрифугах. Тогда из (6.23) можно показать, что давление на внутренний слой осадка р₀ будет равно

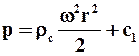, (9.34) 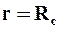, ,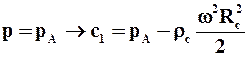(9.35)

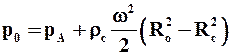(9.36)

или 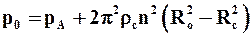, (9.37)

где р_А – давление в газовой фазе внутри барабана. Учитывая, что давление на внешней поверхности фильтровальной перегородки также равно р_А, которое, как правило, равно атмосферному, получим движущую силу процесса центробежного фильтрования в первом периоде:

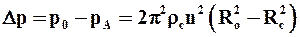. (9.38)

Найденный перепад давлений можно подставить в уравнения (9.20) или (9.23).

В промышленных фильтрующих центрифугах значениеDр достигает 1 – 1,5 МПа. При таких высоких давлениях сжимаемые осадки сильно уплотняются и их гидравлическое сопротивление становится очень большим. Поэтому суспензии, образующие сжимаемые осадки, не рекомендуется разделять на фильтрующих центрифугах. Во втором и в третьем периодах жидкость удаляется из осадка за счет центробежных сил. Описание кинетики при этом имеет сложный характер. Продолжительность центробежного фильтрования в большинстве случаев определяют на базе экспериментальных данных.

Определение производительности фильтров и продолжи-тельности процессов фильтрования. Расчет периодических фильтров сводится к определению производительности фильтра с известной поверхностью фильтрования либо к определению количества фильтров с выбранной поверхностью фильтрования, обеспечивающей заданную производительность.

Производительность одного фильтра, работающего при Dр = const, определяется следующим образом. Время фильтрования t находится из уравнения (9.26):

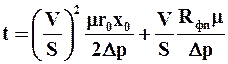. (9.39)

С учетом (9.21) 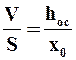уравнение (9.39) преобразуется к виду

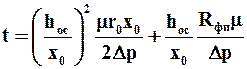. (9.40)

По формуле (9.40) можно определить время (продолжительность) фильтрования, если задана высота слоя осадка, которая зависит от конструкции фильтра и других факторов. Константы фильтрования определяются экспериментальным путем. Время (продолжительность) промывки осадка определяется исходя из уравнения (9.30):

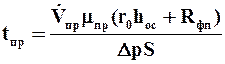, (9.41)

где 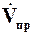– объемный расход промывной жидкости; m_пр – вязкость промывной жидкости; Dр – перепад давления, при котором производится промывка. 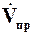определяется по заданному удельному объему промывной жидкости на 1 м³ осадка u_пр:

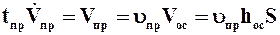, (9.42)

где 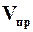– объем промывной жидкости.

Обозначим через t_в.о. продолжительность других вспомогательных операций (сушка осадка, загрузка фильтра, выгрузка осадка и др.) Общая продолжительно работы, учитывающая продолжительность всех осуществляемых операций, будет

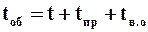. (9.43)

С учетом времени t_об средняя производительность по фильтрату равна

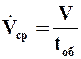, (9.44)

где V определяется по уравнению (9.21), .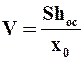

При заданной суточной производительности фильтровальной установки V_уст число циклов фильтрования на одном фильтре k_ц, которое необходимо осуществить для обеспечения суточной производительности V_уст , будет

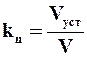. (9.45)

Число циклов фильтрования k₁, которое можно провести на одном фильтре в сутки:

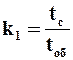, (9.46)

где t_с –рабочая продолжительность суток. Уравнения (9.45) и (9.46) позволяют определить необходимое число фильтров N:

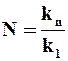. (9.47)

Расчет барабанного вакуум-фильтра непрерывного действия ведется с учетом стандартного распределения поверхности фильтра на технологические зоны. В начале расчета задаются значения: углов сектора (зоны) предварительной сушки осадка, осуществляемой на выходе из зоны фильтрования (j_с1); зоны съема осадка j₀; зоны регенерации фильтровальной перегородки j_р и мертвых зон j_м1, j_м2, j_м3, j_м4, (находящихся между технологическими зонами), в которых ячейки отключены от источников вакуума и сжатого газа. Ориентировочную частоту вращения барабана, обеспечивающую образование осадка заданной толщины (фильтрование), его промывку и сушку, определяют по уравнению

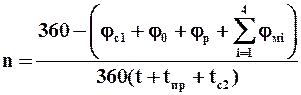, (9.48)

где t, t_пр, t_с2 – соответственно время фильтрования, промывки и сушки осадка после промывки.

Время (продолжительность) фильтрования определяется по уравнению (9.40), а время промывки осадка – по уравнению (9.41), при этом удельный объем промывной жидкости должен быть предварительно экспериментально определен. Продолжительность сушки осадка после промывки задается также из экспериментальных данных.

Время полного цикла работы фильтра t_ц представляет величину, обратную частоте вращения барабана 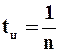.Общую поверхность фильтрования S_об находят по зависимости

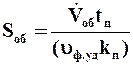, (9.49)

где 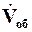– заданная производительность по фильтрату, м³/с; k_п – поправочный коэффициент, учитывающий необходимость увеличения поверхности из-за повышения сопротивления фильтровальной перегородки при многократном ее использовании (k_п » 0,8); u_ф.уд – удельный объем фильтрата, получаемый с 1 м² фильтровальной перегородки за время фильтрования:

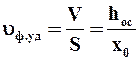. (9.50)

По найденному значению S_об по каталогу выбирают типоразмер фильтра и определяют число фильтров. Затем проверяют пригодность выбранного фильтра. Устанавливают соответствие рассчитанной частоты вращения барабана диапазону частот, указанному в каталоге; сравнивают рассчитанный и стандартный углы сектора (зоны) фильтрования. Если частота выходит за пределы указанного диапазона или рассчитанный угол фильтрования больше стандартного, следует повторно выполнить расчеты, задавшись другой высотой слоя осадка.

После этого производят уточненный расчет фильтра. Принимают по каталогу данные распределения технологических зон. Частоту вращения барабана выбирают наименьшую из рассчитанных по следующим формулам:

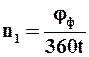, (9.51)

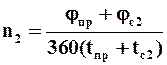, (9.52)

где j_ф – угол зоны (сектора) фильтрования; j_пр – угол сектора промывки; j_с2 – угол сектора сушки осадка после промывки.