Расчет соединений, работающих на изгиб и сложное сопротивление

Примеры соединений, работающих на изгиб, показаны на рис. 4.11 а, б. Если шов выполнен с подготовкой кромок (рис. 4.11.а), то его размеры (расчетная толщина шва) не отличаются от размеров привариваемой полосы. Поэтому напряжения в шве при действии только изгибающего момента М определяются по формуле

σ = М/W ≤ [ σ']_р, (4.23)

где W = s·h²/6; [σ']_р - допускаемое напряжение растяжения сварного соединения;

М - изгибающий момент.

При действии изгибающего момента М и продольной силы Р (рис. 4.11 а, б)

σ = М/W + Р/F, (4.24)

где F = s·h.

Если полоса приварена двумя вертикальными угловыми швами (рис. 4.11 б), то напряжение в плоскости прикрепления О - О (рис. 4.11 в) будет

σ = М/Wс, (4.25)

где Wс - момент сопротивления угловых швов. В плоскости О - О момент сопротивления двух сварных швов высотой h и катетом К равен

Wс = Кh²/6. (4.26)

При этом следует иметь в виду два обстоятельства.

Во-первых, разрушение угловых швов обычно происходит не по плоскости О – О, а по направлению линии ОА, проходящей под углом 45° к плоскости привариваемой полосы.

Поэтому расчетный момент сопротивления угловых швов принимают по меньшему сечению; он будет равен

Wс = 2βКh²/6 (4.27)

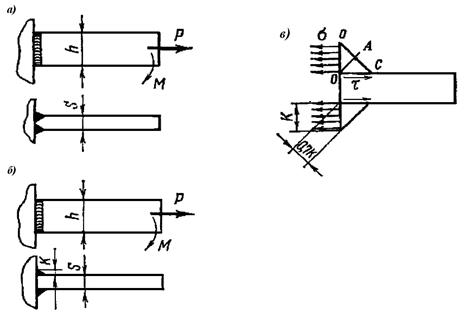
Рис. 4.11. Схема соединений:

а, б – швы, работающие на сложное сопротивление, в том числе на изгиб;

в - схема нагружения углового шва

Во-вторых, расчет прочности швов следует производить не по допускаемым нормальным напряжениям (плоскости О - О), а по напряжениям на косой плоскости (линия ОА). Значение этих напряжений ограничивают допускаемым напряжением на срез [τ']. Таким образом, расчетное напряжение в швах (рис. 4.11 б) от момента М определяют по формуле

τ = М/ Wс ≤ [ τ']. (4.28)

При действии в этом соединении момента М и продольной силы Р расчетное касательное напряжение в угловых швах (рис. 4.11 б) равно

τ = М/ Wс +Р/ Fс ≤ [ τ']. (4.29)

где Fс - площадь сечения угловых швов.

В швах, имеющих форму равнобедренного треугольника минимальная толщина, как бисектрисса прямого угла, будет равна 0,7 К, а площадь среза двух угловых швов Fс =2·0,7 К·h.

Рассмотрим расчет прочности швов, лежащих в плоскости изгибающего момента (рис. 4.12).

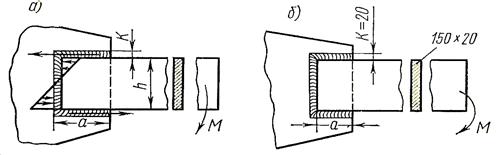
Рис. 4.12. Сварные соединения в плоскости изгибающего момента М: а – схема расчета швов; б – пример расчета по способу расчленения соединения

Расчет прочности проведем по способу расчленения соединения на составляющие. Принимаем, что момент М уравновешивается моментом пары сил в горизонтальных швах Мг и моментом защемления вертикального шва Мв (рис. 4.12 а):

М = Мг + Мв. (4.30)

Допустим, что швы имеют форму равнобедренного треугольника. В горизонтальных швах образуется пара сил. Ее момент равен

Мг = τβКа(h + К). (4.31)

Момент в вертикальном шве вычисляем по формуле

Мв = τβКh² /6. (4.32)

По формуле (3.43),

М = τβКа(h + К) + τβКh²/6, (4.33)

откуда касательное напряжение равно

τ = М/[βКа(h + К) + τβКh² /6] ≤ [τ' ]. (4.34)

Пользуясь уравнением (3.47) при конструировании соединения, легко определить требуемую длину швов а или катет К.

Пример расчета. Сконструировать прикрепление полосы сечением 150Х20 мм вертикальными и горизонтальными швами, равнопрочное целому элементу при изгибе (рис. 4.12 б), допускаемое напряжение [σ]р; сварка полуавтоматическая (β = 0,8); [τ'] = 0,65 [σ]_р.

Момент, допускаемый в полосе, равен М = [σ]_р W = [σ]_р sh²/6.

Момент, допускаемый в вертикальном шве при К = 20 мм и τ' == 0,65 [σ]_р,

равен

М = 0,65 [σ]_р βКh²/6,

Момент, допускаемый в горизонтальных швах, вычисляется по формуле

Мr = М - Мв.

Усилие на один горизонтальный шов равно Р_г = Мг/( h + К) = =[σ]_р h² (s - 0,52К)/[6(h + К)].

Требуемая длина горизонтального шва при К = 20 мм определяется по формуле

а = Р_г /[ τ' ] βК =[σ]_р h² (s - 0,52К)/[3,12 [σ]_р (К + h) К ]≈0,02 м.

Из конструктивных соображений можно принять а = 50 мм.

При рассмотрении прочности прикреплений элементов, работающих на изгиб, будем предполагать, что угловые швы имеют форму равнобедренного треугольника. Расчет прочности производится на срез в плоскости, совпадающей с биссектрисой прямого угла и равной по площади βКа, где К - катет шва, а - длина шва.

Определим напряжения в сварном соединении, прикрепляющем балку прямоугольного поперечного сечения, работающую на изгиб, относительно оси х- х (рис. 4.13, а).

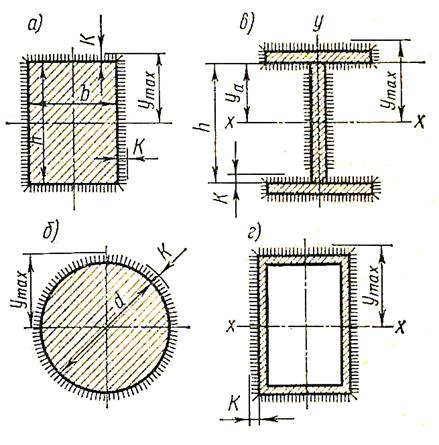
Рис. 4.13. Сварные соединения элементов, обваренных по периметрам угловыми швами: а – прямоугольное сечение; б – круглое сечение; в – двутавровое сечение; г – коробчатое сечение

Соединение сконструировано с угловыми швами, охватывающими профиль по периметру. Нормальные напряжения в балке вызывают касательные напряжения τ в швах:

τ = М/Wc ≤ [τ']. (4.35)

Момент сопротивления

Wс = Iс/y_max, (4.36)

где Iс - расчетный момент инерции периметра швов относительно оси Х-Х. С учетом возможного разрушения по наименьшему сечению Iс = I·β,

где I - момент инерции периметра швов, т. е.

Iс = β {2Кb [(h + К)/2]² + 2К³b/12 + 2К (h + 2К)³/12}; (4.37)

y_max = h/2+К. (4.38)

Для круглого поперечного сечения (рис. 4.13 б)

Iс = β [π (d + 2К)⁴/64 - πd⁴/64]; (4.39)

y_max = d/2+К. (4.40)

Расчет прочности прикрепления произвольных профилей двутавровых, коробчатых (рис. 4.13 е, г), тавровых и других производится так же, как в случаях, рассмотренных выше, на основе формул (4.35) и (4.36).

Если элемент работает при сложном сопротивлении - изгибающем моменте М и продольной силе N, то суммарное напряжение в соединении равно

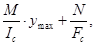τ = (4.41)

где F_c – расчетная площадь среза всех сварных швов:

F_c = β·K·L, (4.42)

где L – длина периметра сварных швов.

Если элементы нагружены поперечными нагрузками, то в них возникают изгибающие моменты М и поперечные силы Q. Напряжения в сварных швах от действия силы Q определяют с учетом следующих допущений: поперечная сила воспринимается только вертикальными швами, распределение напряжений по длине вертикальных швов равномерно. Таким образом, среднее напряжение в шве от поперечной силы равно

τ_Q = Q / F_B, (4.43)

где F_B - расчетная площадь вертикальных швов.

На уровне верхней кромки вертикального листа в швах следует проверить результирующие напряжения от действия момента и поперечной силы.

Напряжение от момента

τ₁ = y_a М / Ic, (4.44)

где y_a - расстояние от оси, проходящей через центр тяжести сечения, до горизонтальной верхней кромки (рис. 4.14).

Напряжение от поперечной силы

τ_Q = Q /(2βKh). (4.45)

Результирующее напряжение равно корню квадратному из суммы квадратов τ₁ и τ_Q:

τ_рез = √τ₁² + τ_Q² (4.46)

Практика расчетов показывает, что проверка прочности по формуле (4.35) является решающей.

Пример расчета.Консольная стальная балка двутаврового профиля (рис. 4.14) прикреплена по периметру угловыми швами с катетом К = 6 мм; продольная сила N = 50 кН; поперечная сила Q = 2,5 кН; сварка полуавтоматическая (β = 0,8) в среде СО₂ проволокой Св-08Г2С с расчетным сопротивлением металла угловых швов R_wf =215 МПа.

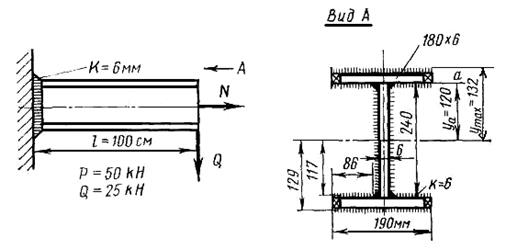
Рис.4.14. Расчет швов соединений при сложном сопротивлении

Момент инерции периметра угловых швов равен

I = 2 · 24³ · 0,6/12 +2 (19 · 0,6³/12 + 19 · 0,6 · 12,9²) + 2(2 · 8,6 · 0,6³/12 + 2 · 8,6 · 0,6· ·11,7²) = 8000 см⁴.

Расчетный момент инерции угловых швов с учетом разрушения по опасной плоскости (β = 0,8) Ic = β· I = 0,8 · 8000 = 6400 см⁴.

Ордината y_a = 12 см. Площадь поперечного сечения всего периметра угловых швов F = 2 · 24 · 0,6 + 2 · 19 · 0,6 + 4 · 8,6 · 0,6=72,2 см².

Расчетная площадь всех сварных швов с учетом разрушения по опасной плоскости равна Fc = F·β = 0,8 · 72,2 = 57,7 см².

Расчетная площадь вертикальных швов с учетом разрушения по опасной плоскости будет F^′_с=2 · 0,8 · 0,6 · 24 ==23,0 см².

Напряжения от изгиба на крайней кромке вертикального листа равны

τ₁=М·y_a /Iс = 0,025 · 1 · 0,12 / (6400 · 10^-8) = 47 МПа.

Напряжение от продольной силы в угловых швах соединения

τ_N = N / Fc = 0,05/(57,7 · 10^-4) = 8,4 МПа.

Суммарное напряжение τ = 47 + 8,4 = 55,4 МПа.

Среднее касательное напряжение в вертикальных швах

τ_Q = 0,025 / 23 ·10^-4 = 10,9 МПа.

Результирующее напряжение при y_a = 12 см

τ_рез = √55,4² + 10,9² = 56,5 МПа.

Напряжение от изгиба при y_max = 13,2 см

τ = М·y_max / Ic = (0,025 · 1 / 6400 · 10 ^-8) · 0,132 = 51,6 МПа.

Суммарное напряжение от М и N при y_max = 13,2 см

τ_сумм = 51,6 + 8,4 = 60,0 МПа < R_wf =215 МПа.