Многопролетные статически определимые шарнирно-консольные балки

Применение многопролетных балок

Многопролетные статически определимые балки применяют для перекрытия смежных пролетов. Вследствие более рационального распределения изгибающих моментов этот тип балок экономичнее, чем система однопролетных самостоятельных балок, перекрывающих те же пролеты и загруженных теми же нагрузками. Например, два смежных пролета длиной по 10 метров перекрыты двумя отдельными однопролетными балками (рис. 3.9 а) и многопролетной статически определимой шарнирно-консольной балкой (рис. 3.9 б). При одинаковой равномерно распределенной нагрузке интенсивностью q=2 т/м распределение изгибающих моментов у многопролетной балки более равномерное, меньше и величина максимального изгибающего момента.

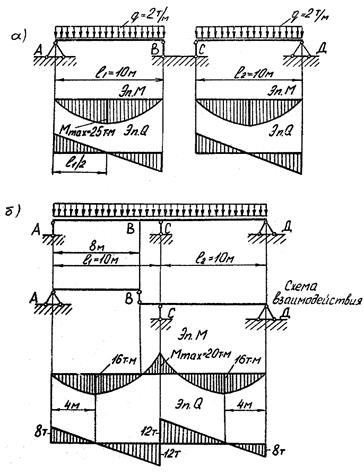
Рис. 3.9. Эпюры М и Q однопролетных и многопролетной балок, перекрывающих одинаковый пролет и нагруженных одинаковой равномерно

распределенной нагрузкой

Типы балок

На практике нашли применение в основном балки двух типов. Первый тип (рис. 3.10 а), состоит из основных двухконсольных ба­лок - АД, ЕН и JМ и подвесных коротких балок - ДE, HJ. Второй тип (рис. 3.10 б) состоит из одной основной (двухконсольной или одноконсольной) балки АД и второстепенных одноконсольных балок ДF, FH, HK. Каждая последующая опирается на консоль предыдущей. Применяются также и балки третьего смешанного типа (рис. 3.10 в).

Расчет этих балок при действии неподвижной нагрузки сос­тоит в построении эпюр изгибающих моментов эп.М и поперечных сил - эп.Q. Для этого необходимо определить усилия во всех опорных стержнях. Следовательно, многопролетная балка статически определима, если количество уравнений равновесия равно количеству опорных стержней (т.е. неизвестных).

С_ОП = Ш + 3, (3.5)

где С_ОП - количество опорных стержней;

Ш + 3 - - количество уравнений; к трем уравне­ниям статики, относящимся к балке в целом (∑X = 0, ∑У = 0, ∑ Mi = 0), можно дополнительно составить столько уравнений, сколько имеется шарниров (Ш), т.к. момент всех сил, приложенных к балке с одной стороны шарнира, относительно оси этого шарнира, равен нулю; шарниры, служащие только для присоединения опорных стержней, в счет не входят.

Отсюда следует, что в статически определимой многопролет­ной балке количество шарниров равно:

Ш = С_ОП - 3.

Отметим, что статическую определимость балки можно прове­рить также с помощью уравнения (3.1).

Шарниры должны быть расположены в балке так, чтобы балка была геометрически неизменяемой, т.е. должны быть соблюдены правила соединения дисков в единую неизменяемую систему.

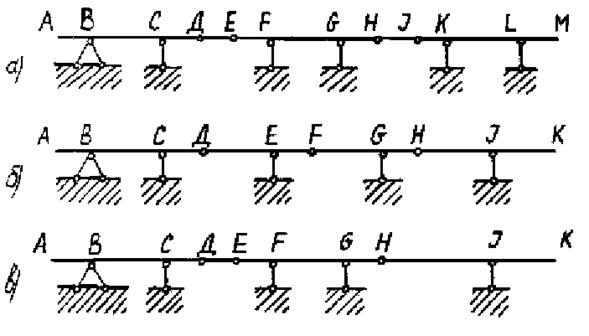
Рис. 3.10. Примеры многопролетных геометрически неизменяемых

и статически определимых балок

Следу­ет при этом помнить, что мгновенно изменяемые системы и близкие к ним недопустимы в реальных сооружениях.

3.3.3. Аналитический способ расчета статически определимых многопролетных балок на неподвижную нагрузку

Как известно, существуют аналитический и графический спо­собы расчета балок. Первому следует отдать пред­почтение как более точному.

Перед расчетом балки необходимо проверить на статическую определимость и геометрическую неизменяемость, а затем составить схему взаимодействия (поэтажную схему) элементов балки. Схема взаимодействия (рис.3.11) позволяет выяснить, какие элементы являют­ся основными, а какие второстепенными, опирающимися на эти основные. При составлении схем взаимодействия необходимо произ­вести перестановку опорных стержней с тем, чтобы все элементы остались статически определимыми и геометрически неизменяемыми. Общее количество связей при этом остается неизменным.

Расчет необходимо начинать всегда с второстепенных элемен­тов. Второстепенные элементы представляют собой или однопролетные бесконсольные балки, опирающиеся на консоли основных элементов (рис. 3.11 а), или одноконсольные однопролетные балки, после­довательно опирающиеся на консоль своего поддерживающего элемента (рис. 3.11 б). Расчет второстепенного элемента заключается в определении опорных реакций и построения эп.М по методике, известной из курса «Сопротивление материалов». После расчета второстепенных элементов необходимо перейти к основным элементам. При этом к нагрузкам, непосредственно действующим на основной (поддержи­вающий) элемент, следует добавить усилия, которые передается отвторостепенных элементов. Эти усилия равны опорным реакциям второстепенных элементов, взятыми с обратными знаками.

Рассчитав все элементы, эпюры моментов объединяют в один чертеж. Эпюры поперечных сил строят для всей балки в целом. Правильность построения эпюр проверяют по известным зависимос­тям между нагрузкой, эпюрой М и эпюрой Q :

Q = dM/dx; tg a = dM/dx; если М(х) = max М(х), то Q = tg a = 0.

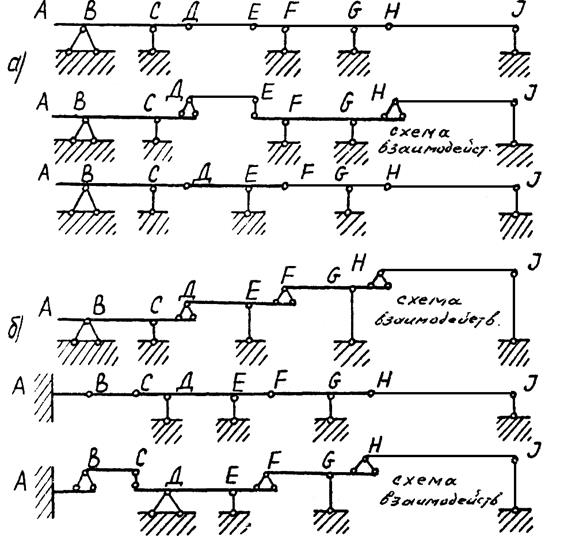
Рис. 3.11. Схема взаимодействия элементов многопролетных балок

Аналитический расчет многопролетной статически определимой балки рассмотрим на примере. Геометрическая схема балки, размеры и нагрузка показаны на рис. 3.12 а; схема взаимодействия показана на рис. 3.12 б.

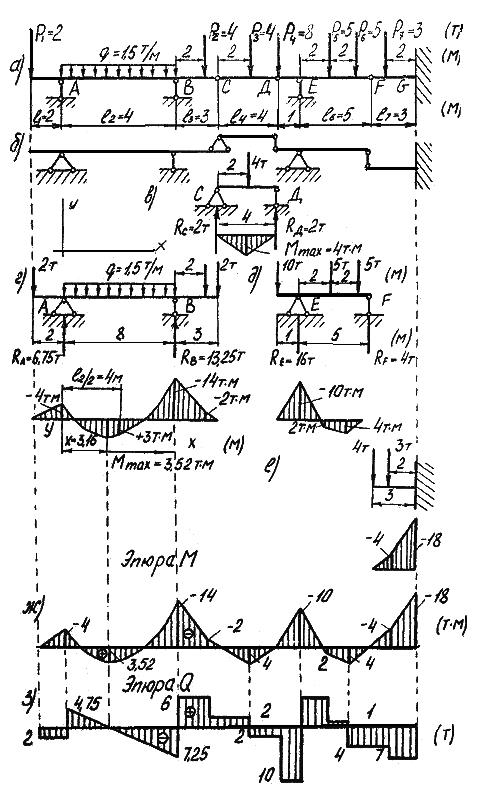
Рис. 3.12. Многопролетная балка с результатами расчета и

графиками эпюр М и Q

_Решение. Из схемы взаимодействия видно, что расчет необ­ходимо начать со второстепенного элемента СД, представляющего собой балку на двух опорах, которая нагружена одной сосредоточенной силой Р₃ = 4т. .

Определяем опорные реакции балки СД R_C = R_D = 2 т.

Определяем величину максимального изгибающего момента (всечении под силой Р₃)

М_max = R_C · L₄/2 = 4 т·м.

Строим эпюру изгибающих моментов для балки СД (рис. 3.12 в).Переходим к балке ABC, добавив к нагрузкам, непосредственно действующим на нее, дополнительное усилие | Р_Д1 | = | R_C| = 2 т, направив еговниз (рис. 3.12 г).

R_A = ? ∑M_B = 0; R_A · L₂ + P₂ · 2 +Р_Д1 · L₃ - q · L₂ · L₂/2 - P₁ (L₁ + L₂) = 0, (3.7)

R_A = 6,75 т.

Опорную реакцию R_В найдем аналогичным образом из уравнения равновесия

∑M_А = 0; R_В = 13,25 т. (3.8)

Для построения эпюры моментов определим опорные моменты

M_А = -2 · 2 = - 4 т·м; M_B = -4 · 2 - 2 · 3 = - 14 т· м.

Момент посредине пролета

М_L2/2 = 6,75 · 4 - 2 · 6 - 1,5 · 4 · 2 = + 3 т·м,

а максимальный изгибающий момент М_max необходимо найти.

Сечение, в котором действует М_max, неизвестно. Определим его положение. Для этого составим выражение поперечной силы в этом сечении и приравняем его к нулю (рис. 3.12, г).

Q_X = -P₁ + R_A - q · X = 0: - 2 + 6,75 - 1,5 · X = 0, (9) или -2 + 6,75 = 1,5 · X, откуда Х = 3,16 м.

Изгибающий момент в этом сечении будет иметь максимальное значение.

Определим величину максимального изгибающего момента

М_max = М_Х = R_A · 3,16 - Р₁· (2 + 3,16) - q · 3,16 · 1,58 = 3,52 т·м. (3.10)

Переходим к балке ДЕF (рис.3.12 д). К нагрузке, непосредствен­но действующей на балку, добавим дополнительное усилие Р_q2 = 2 т . Определив опорные реакции R_Е и R_F, построим эпюру моментов.

Переходим к последнему элементу - консольной балке FG. Определив опорную реакцию R_G , построим эпюру моментов, рис. 3.12, е.

Соединяем все эпюры в единую общую, рис.3.12, ж.

Эпюры поперечных сил строим для всей балки А - G в целом по правилам, известным из курса «Сопротивление материалов» (рис. 3.12 з).

Правильность построения эпМ и эпQ можно проверить, как известно, по зависимостям, существующим между внешней нагруз­кой, эпюрой моментов и эпюрой поперечных сил. Напоминаем основ­ные зависимости:

а) в сечениях, где приложены сосредоточенные силы, эпМ имеет переломы, а эпQ - скачки на величину силы.

б) в пределах приложения равномерно распределенной нагрузки эпМ имеет криволинейное очертание (по параболе).

в) поперечная сила равна первой производной момента по X

Q= dM/dx (3.11)

или при графическом изображении эпМ, поперечная сила равна тангенсу угла α между осью X и касательной к эпюре М в соответствующей точке. Поэто­му в сечениях, где М = max M, tg α = 0 и попереч­ная сила Q переходит через ноль.

Знаки для величин М и Q условимся связывать с характе­ром деформации балки при действии внешних сил. Если в сечении балки m-n (рис. 3.13 а), балка деформирована выпуклостью вниз (нижние волокна растянуты), то изгибающий момент М положителен. Если балка деформирована выпуклостью вверх (рис. 3.13 б), -М отрицателен. На рис. 3.13 в, г показан характер деформаций при действии соответственно положительных и отрицательных попе­речных сил.

Правила, устанавливающие знаки изгибающих моментов М и по­перечных сил Q, действующих в сечениях балок, носят условный характер. Но при построении эп М и эп Q и проведении расчетов эти правила должны неукоснительно выполняться.

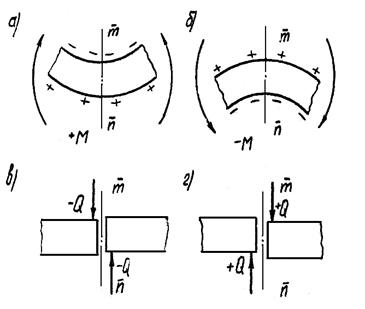
Рис. 3.13. Правила знаков моментов М и поперечных сил Q

Условимся также, что при построении эпюр М и Q положительные и отрицательные ординаты графиков будем откладывать так, как показано на рис. 3.13.