Анализ геометрической структуры

В каждой неизменяемой статически определимой системе степень свободы должна быть равна нулю ( W = 0).

Соблюдение этого условия совершенно необходимо, но недостаточно; Например, в балках, показанных на рис. 3.5 а,б, одинаковое количество дисков (D= 3), шарниров (Ш =2) опорных стержней (С_ОП = 5).

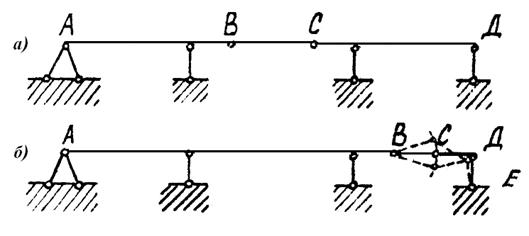
Рис. 3.5. Примеры для проверки структур балок

на геометрическую неизменяемость

Необходимое условие геометрической неизменяемости W =3 · 3 - 2 · 2 -5= 0 выполняется для обеих балок. Однако первая балка, рис. 2.5 а, геометрически неизменяема, а вторая, рис.3.5 б, изменяема, так как шарнир С может свободно перемещаться вниз или вверх.

Поэтому, убедившись, что необходимое условие W =0 выпол­нено, провести анализ геометрической структуры рассматриваемой системы. Анализ состоит, в основном, в проверке вы­полнения правил соединения отдельных дисков между собой.

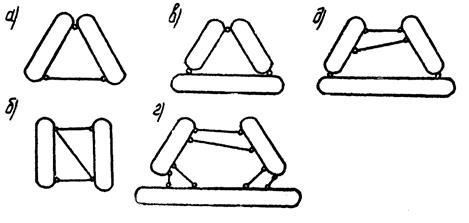
Рис. 3.6. Правила соединения дисков в единую неизменяемую систему:

а - два диска соединены шарниром и стержнем; б - два диска соединены тремя непараллельными стержнями; в - три диска соединены тремя шарнирами; г, д - три диска соединены эквивалентным количеством стержней (один простой шарнир эквивалентен двум соединительным стержням)

Правила соединения дисков в единую неизменяемую систему:

1.Два диска должны быть соединены шарниром и стержнем (рис. 3.6 а), или тремя стержнями (рис. 3.6, б).

2.Три диска должны быть соединены тремя шарнирами (рис 2.6 в), или эквивалентным количеством стержней (рис.3.6 г, д), при этом нужно помнить, что по количеству налагаемых связей один простой шарнир эквивалентен двум стержням.

Проведем анализ геометрической структуры балки (рис.3.5 б), применяя рассмотренные правила. Диск АВ соединен с землей четы­рьмя стержнями и образует с ней единую неизменяемую систему. Диск СД присоединен к ней двумя стержнями СВ и ДЕ. В соответ­ствии с правилом 1 для неизменяемости необходимо три соединяю­щих стержня. Нетрудно видеть, что в балке (рис. 3.5 а), правила соединения дисков в единую неизменяемую систему выполнены.

3.2.3. «Мгновенно» изменяемые системы

Применяя правила соединения дисков в единую неизменяемую систему, необходимо учитывать следующее. В случае соединения двух дисков тремя соединяющими стержнями, стержни не должны пересекаться в одной точке (рис. 3.7 а). Если соединяющие стержни пересекаются в одной точке, мы получаем мгновенно изменяемую систему, так как в точке пересечения возникает мгновенный центр вращения дисков (одного относительно другого). Мгновенно изме­няемые системы не могут использоваться на практике. Рассмотрим равновесие системы (рис. 3.7 а), с помощью уравнения статики

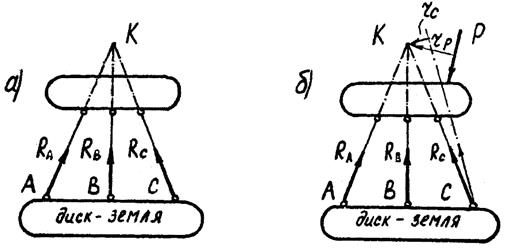
Рис. 3.7. Мгновенно изменяемая (а) и

близкая к мгновенно изменяемой система (б)

∑ М_К = 0: R_A · 0 + R_B · 0 + R_C · 0 = 0.

Уравнение выполняется при любых значениях опорных реакций (усилий в стержнях), т.е. значения усилий R_A, R_B и R_C неопределенны по значениям. При отсутствии внешней нагрузки на неизменяемую систему усилия R_A, R_B и R_C должны быть равны нулю однозначно. Приложим к системе силу Р и преобразуем ее в близкую к мгновенно изменяемой так как показано на рис.3.7 б. Рассмотрим равновесие системы с помощью уравнения

∑ М_К = 0: -R_C · r_C + P · r_P = 0; R_C = P· r_P/ r_C. (3.3)

Приближая систему к мгновенно изменяемой, получаем r_C → 0 и R_C → ∞,

что, соответственно, недопустимо.

Вывод: в системах, близких по геометрической структуре к мгновенно изменяемым, при действии внешней нагрузки конечной величины возникают усилия, стремящиеся к бесконечности. В реаль­ных сооружениях такие системы недопустимы.

В случае соединения трех дисков соединяющие шарниры (дей­ствительные или условные) не должны располагаться на одной пря­мой (рис.3.8 а). Если три диска соединяются стержнями, то стержни не должны пересекаться в одной точке, рис. 3.8. Пренебрегая эти­ми условиями, мы можем получить мгновенно изменяемую систему. Например, имеем систему, показанную на рис. 3.8 в. Считая землю диском, это система, состоящая из трех дисков, соединенных тре­мя шарнирами, из которых шарниры А и С - условные. Система явля­ется статически определимой и геометрически неизменяемой. Она превратится в мгновенно изменяемую, если все три шарнира А, В и С будут находиться на одной прямой.

Будем приближать заданную систему к мгновенно изменяемой, т.е. будем опускать узел В на прямую АС. При этом угол α →π/2, и возникает определенная ситуация.

Заметим, что на практике ситуация, рассмотренная ниже, мо­жет возникнуть в случае, если высоту стропильных ферм, несущих кровлю здания, чрезмерно уменьшить в коньке, приблизив угол меж­ду стержнями АВ и ВС к 180°. Причем введение в конструкцию фер­мы затяжки, т.е. стержня, соединяющего опорные узлы А и С, не меняет дела.

Как мы увидим далее, уменьшение высоты стропильных ферм в коньке приводит к увеличение усилий сжатия в стропильных «ногах» - стержнях АВ и ВС, что заставляет, в свою очередь, увеличивать их сечение. В итоге стропильные фермы оказываются очень тяжелыми. Впрочем, вернемся к ситуации, ког­даα →π/2 (рис. 3.8 в).

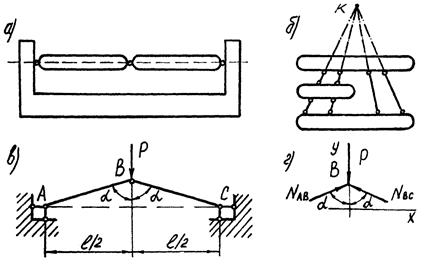
Рис.3.8. Примеры стержневых систем, недопустимых в строительных конструкциях:

а - шарниры расположены на одной прямой; б - оси стержней пересекаются в одной точке; в - недопустимая величина угла α →π/2; г - схема к расчету усилий, сходящихся в узле В

Рассмотрим ее, для этого вырежем узел В и составим урав­нение равновесия сил, сходящихся в узле:

∑Y = 0: -Р + N_AB · Cos α + N_BC · Cos α = 0;

N_AB = N_BC = P · 1/ Cos α, (3.4)

Если α →π/2, то Cos α →0 и N_AB (N_BC) → ∞.

Вывод: не только мгновенно изменяемые, но и близкие к ним системы не могут применяться в реальных сооружениях и конструк­циях.

Анализ на статическую определимость и геометрическую неиз­меняемость является обязательным для всех сварных металлических конструкций перед их расчетом на прочность, жесткость и устойчивость. Геометрически изменяемые и мгновенно геометрически из­меняемые системы не могут использоваться в сооружениях в качестве несущих конструкций.