Исследование плоских систем на статическую определимость и геометрическую неизменяемость

Общие положения

Одним из основных, безусловно, необходимых свойств сварных металлических конструкций, как несущих сооружений, является геометрическая неизменяемость. Это означает, что в конструкции под действием внешней нагрузки не может быть взаимных перемещений элементов и частей. Иначе говоря, каждый элемент конструкции имеет степень свободы, равную нулю.

В то же время следует отметить, что под действием внешней на­грузки элементы конструкции упруго изменяют свои форму и разме­ры. Так, например, в ферме растянутые элементы удлиняются, а сжатые укорачиваются, а ферма в целом получает прогиб. Эти изме­нения представляют собой нормальное явление, происходящее со всеми твердыми телами под нагрузкой и обусловленное упругой деформацией материала. После снятия нагрузки элементы и ферма принимают исходные форму и размеры. Упругие деформации элементов реальных металлических конструкций обычно не превышают 0,1%.

Изменяемые системы могут изменить свою форму под действием бесконечно малых нагрузок без изменения размеров элементов толь­ко за счет их взаимного перемещения. В качестве примера можно при­вести шарнирный четырехугольник и однопролетную балку, имеющую в пролете шарнир, (рис.3.1 а,б). Если четырехугольник раскрепить ди­агональным стержнем, (рис. 3.1 в), а из балки убрать шарнир (рис.3.1 г), то эти системы превратятся в геометрически неизменяемые.

Понятие «диск». В статике сооружений диском называют такую часть системы, в геометрической неизменяемости которой нет сомнений. Простейшими дисками являются стержень и шарнирный стержневой треугольник (рис. 3.2 а, б). Ферма АВС, приведенная на рис. 3.2 б, может также рассматриваться как диск. Обобщенное изо­бражение диска, независимо от внутренней структуры, показано на рис. 3.2 г. «Земля», как неизменяемое основание сооружения, также считается диском.

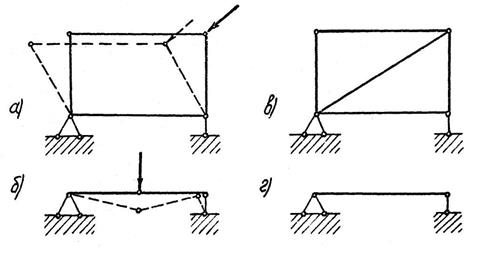
Рис. 3.1. Примеры геометрически изменяемых (а, б)

и неизменяемых (в, г) стержневых систем

Понятие «степень свободы». В статике сооружений под степенью свободы диска понимают число геометрических параметров, которые могут изменяться независимо друг от друга при перемещении этого диска. В плоской системе координат точка имеет степень свободы, равную двум, так как ее положение определяется двумя координатами. Стержень (диск) в плоскости имеет степень свободы, равную трем, так как положение стержня определяется тремя геометрическими параметрами (Х_А,У_А, угол α) которые при перемещении стержня могут изменяться независимо друг от друга (рис. 3.3 а). Отсюда, следует, что число степеней свободы стержней, не связанных между собой, в плоскости равно утроенному количеству стержней. Шарнир, связывающий два стержня, снижает степень свободы системы на два (рис.3.3 в).

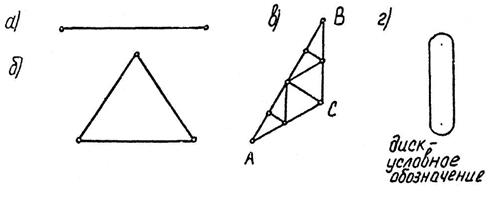
Рис. 3.2. Примеры дисков

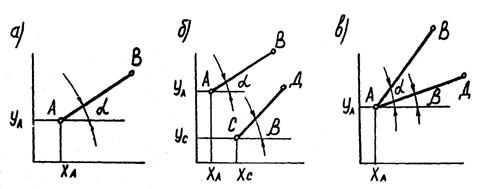
Рис. 3.3. Степень свободы стержней: а - стержень в плоскости имеет 3 степени свободы; б - два отдельных стержня имеют 6 степеней свободы; в - два стержня соединенные общим шарниром имеют 4 степени свободы

Действительно, суммарное число степеней свободы двух стержней, не связанных между собой, равно шести. Если мы соединим их об­щим шарниром А, стержни могут перемещаться только совместно. По­ложение шарнира А определяется двумя координатами, которые могут изменяться независимо друг от друга. Кроме того, каждый стержень независимо один от другого может поворачиваться около шарнира А. Следовательно, степень свободы системы, приведенной на рис.3.3 в, равна четырем.

Таким образом, шарнир, соединяющий два диска, (простой шар­нир) уменьшает степень свободы системы на две единицы. Если шар­нир соединяет три и более дисков, его называют сложным. Если сложный шарнир соединяет N дисков, то по числу налагаемых связей он эквивалентен (N-1) простому шарниру. Каждый опорный стер­жень уменьшает степень свободы системы на единицу.

На основании вышеизложенного можно записать

W= 3D- 2Ш - С_ОП , (3.1)

где W - степень свободы системы; D - количество дисков; Ш- количество простых шарниров (шарниры, присоединяющие к диску только опорные стержни, в счет не входят); С_ОП -количество опорных стержней.

На рис. 3.4 приведены примеры стержневых систем для анализа степени свободы W.

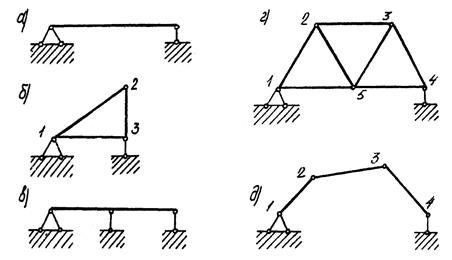
Рис. 3.4. Примеры стержневых систем для анализа степени свободы W

Если W = 0 - система неизменяема и статически определима;

если W> 0 - система изменяема; если W<0 - система неизменяема, но статически неопределима.

Для системы, приведенной на рис. 3.4 а, D = 1; Ш = 0; С_ОП = 3; получаем

W = 3 ·1 - 2 · 0 -3 = 0 ; система неизменяема и статически определима.

Для системы, приведенной на рис. 4 б, D = 3; Ш = 3 (шарниры I и 3 учитываем, так как они не только присоединяют опор­ные стержни, но и соединяют между собой диски); С_ОП = 3, отсюда получаем W = 3 · 3 - 2 · 3 - 3 = 0; система неизменяема и стати­чески определима. В данной системе шарнирный треугольник в целом также является диском, поэтому можно записать D = 1; Ш = 0; С_ОП = 3, получаем также W = 0.

Анализ, как мы видим, приводит к тому же результату.

Для системы, приведенной на рис. 3.4 в, D = 1; Ш = 0; С_ОП = 4, получаем

W = 3 ·1 - 2 · 0 - 4 = -1; система неизменя­ема и один раз статически неопределима.

Для системы, приведенной на рис. 3.4 г, D = 7; Ш = 9 (шарниры I и 4, соединяющие по два диска, являются простыми; шарниры 2 и 3, соединяющие по три диска, являются сложными и каждый эквивалентен 3-1 = 2 простым шарнирам; шарнир 5 эквивален­тен 4 - 1= 3 простым шарнирам;

Ш = 1 + 1 + 1 + 2 + 2 + 3 = 9; С_ОП = 3, получаем

W = 3 · 7- 2 · 9 - 3 = 0; система неизменяема и статически определима.

Для системы, приведенной на рис. 3.4 д, D = 3; Ш = 2 (шарниры 1 и 4 служат для присоединения только опорных стержней и в счет не входят); С_ОП = 3, получаем W = 3 · 3- 2 · 2 - 3 = 2; система изменяема и имеет степень свободы, равную двум. Анализ изменяемости системы, не связанной опорными стержнями с землей, проводится при помощи формулы

V= 3D- 2Ш - 3, (3.2)

где V - степень изменяемости системы, характеризующая взаимные перемещения элементов системы.

Если V = 0, то в системе взаимные перемещения составляющих ее элементов отсутствуют, т.е. система внутренне геометрически неизменяема.

При этом нужно иметь в виду, что система в целом может пе­ремещаться в плоскости со степенью свободы, равной трем. Анализ на внутреннюю геометрическую неизменяемость систем, присоединенных опорными стержнями к земле, можно провести, предварительно отбро­сив опорные стержни. Это можно делать, если число опорных стерж­ней С_ОП = 3. Если число опорных стержней С_ОП ≥ 4, анализ сис­тем на геометрическую неизменяемость можно проводить только в связи с землей.