Формализованные методы прогнозирования

Прогнозирование с помощью формализованных методов осуществляется по строго определенному алгоритму, форме.

Формализованные методы базируются на математической теории, которая обеспечивает повышение достоверности и точности прогнозов, сокращает сроки их выполнения и облегчает обработку информации и оценку результатов. К формализованным методам прогнозирования относятся методы экстраполяции и методы моделирования (рис. 4).

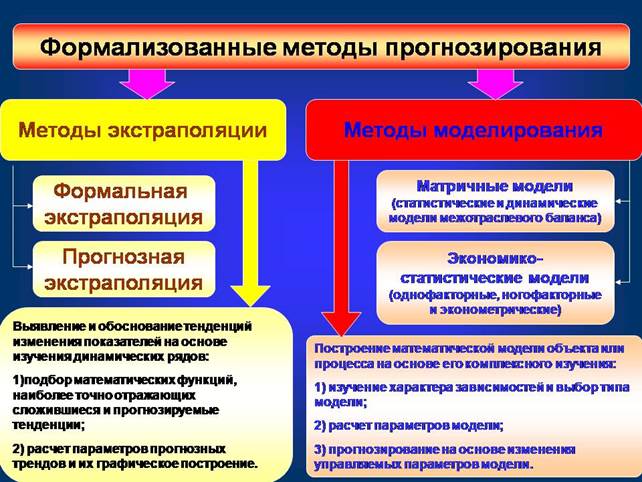
Рис. 4. Формализованные методы прогнозирования.

Сущность экстрапо­ляции заключается в изучении сложившихся в прошлом и нас­тоящем устойчивых тенденций развития объекта прогноза и переносе их на будущее.

Различают формальную и прогнозную экстраполяцию. Формальная базируется на предположении о сохранении в бу­дущем прошлых и настоящих тенденций развития объекта про­гноза; при прогнозной фактическое развитие увязывается с ги­потезами о динамике исследуемого процесса с учетом изменений влияния различных факторов в перспективе.

Методы экстраполяции являются наиболее распространенными и проработанными. Основу экстраполяционных методов прогнозирования составляет изучение динамических рядов. Динамический ряд — это множество наблюдений, полученных последовательно во времени.

В экономическом прогнозировании широко применяется метод математической экстраполяции, в математическом смысле означающий распространение закона изменения фун­кции из области ее наблюдения на область, лежащую вне отрезка наблюдения. Тенденция, описанная некоторой функцией от времени, называется трендом. Тренд - это длительная тенден­ция изменения экономических показателей. Функция пред­ставляет собой простейшую математико-статистическую (трендовую) модель изучаемого явления.

Следует отметить, что методы экстраполяции необходимо применять на начальном этапе прогнозирования для выявле­ния тенденций изменения показателей.

Метод подбора функций — один из распространенных ме­тодов экстраполяции. Главным этапом экстраполяции тренда является выбор оптимального вида функции, описывающей эмпирический ряд. Для этого проводятся предварительная обработка и преобразование исходных данных с целью облег­чения выбора вида тренда путем сглаживания и выравнива­ния временного ряда. Задача выбора функции заключается в подборе по фактическим данным (x_i, y_i) формы зависимости (линии) так, чтобы отклонения (∆_i) данных исходного ряда y_i от соответствующих расчетных y_i, находящихся на линии, бы­ли наименьшими. После этого можно продолжить эту линию и получить прогноз.

где n – число наблюдений.

Выбор модели осуществляется с помощью специально раз­работанных программ. Есть программы, предусматривающие возможность моделирования экономических рядов по 16-ти функциям: линейной (у = а + bх), гиперболической различных типов (у = а + b/х), экспоненциальной, степенной, логарифмической и др. Каждая из них может иметь свою, специфическую область применения при прогнозировании экономических явлений.

Так, линейная функция (у = а + bх) применяется для описания процессов, равномерно развивающихся во времени. Параметр b (коэффициент регрессии) показывает скорость изменения прогнозируемого у при изменении х.

Гиперболы хорошо описывают процессы, характеризующиеся насыщением, когда существует фактор, сдерживающий рост прогнозируемого показателя.

Модель выбирается, во-первых, визуально, на основе сопоставления вида кривой, ее специфических свойств и качественной характеристики тенденции экономического явления; во-вторых, исходя из значения критерия. В качестве критерия чаще всего используется сумма квадратов отклонений S. Из со­вокупности функций выбирается та, которой соответствует минимальное значение S.

Прогноз предполагает продление тенденции прошлого, вы­ражаемой выбранной функцией, в будущее, т.е. экстраполяцию динамического ряда. Программным путем на ЭВМ определяется значение прогнозируемого показателя. Для этого в формулу, описывающую процесс, подставляется величина периода, на который необходимо получить прогноз.

В связи с тем, что этот метод исходит из инерционности экономических явлений и предпосылок, что общие условия, определяющие развитие в прошлом, не претерпят существен­ных изменений в будущем, его целесообразно использовать при разработке краткосрочных прогнозов обязательно в соче­тании с методами экспертных оценок. Причем динамический ряд может строиться на основании данных не по годам, а по месяцам, кварталам.

Экстраполяция методом подбора функций учитывает все данные исходного ряда с одинаковым «весом». Классический метод наименьших квадратов предполагает равноценность исходной информации в модели. Однако, как показывает опыт, экономические показатели имеют тенденцию «старе­ния». Влияние более поздних наблюдений на развитие про­цесса в будущем существеннее, чем более ранних. Проблему «старения» данных динамических рядов решает метод экспо­ненциального сглаживания с регулируемым трендом. Он поз­воляет построить такое описание процесса (динамического ряда), при котором более поздним наблюдениям придаются большие «веса» по сравнению с более ранними, причем «веса» наблюдений убывают по экспоненте. В результате создается возможность получить оценку параметров тренда, характери­зующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения.

Скорость старения данных характеризует параметр сглажи­вания а. Он изменяется в пределах 0 < а < 1.

В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного ряда наблюдений: чем больше а, тем больше вклад последних наблюдений в фор­мирование тренда, а влияние начальных условий быстро убы­вает.

При малом а прогнозные оценки учитывают все наблюде­ния, при этом уменьшение влияния более «старой» информации происходит медленно, т.е. чем меньше а, тем дан­ные более стабильны, и наоборот.

В области экономического прогнозирования наиболее употребимы пределы
0,05 < а < 0,3. Значение а в общем случае должно зависеть от срока прогнозирования: чем меньше срок, тем большим должно быть значение параметра.

Этот метод реализуется на ЭВМ с помощью специально раз­работанных программ в блоке «временные ряды», который яв­ляется составной частью пакета экономических расчетов.

Моделирование предполагает конструирование модели на основе предварительного изучения объекта или процесса, выделения его существенных характеристик или признаков. Прогнозирование экономических и социальных процессов с использованием моделей включает разработку модели, ее эк­спериментальный анализ, сопоставление результатов про­гнозных расчетов на основе модели с фактическими данными состояния объекта или процесса, корректировку и уточнение модели.

В зависимости от уровня управления экономическими и со­циальными процессами различают макроэкономические, ме­жотраслевые, межрайонные, отраслевые, региональные модели и модели микроуровня (модели развития фирмы).

По аспектам развития экономики выделяют модели прогнозирования воспроизводства основных фондов, трудовых ресурсов, цен и др. Существует ряд других признаков классификации моделей: временной, факторный, транспортный, производственный.

В современных условиях развитию моделирования и практическому применению моделей стала придаваться особая значимость в связи с усилением роли прогнозирования и переходом к индикативному планированию.

Рассмотрим некоторые из наиболее разработанных экономико-математических моделей, получивших широкое применение в практике прогнозирования экономики,

К матричным моделям относятся модели межотраслевого баланса (МОБ): статические и динамические. Первые предназ­начены для проведения прогнозных макроэкономических рас­четов на краткосрочный период (год, квартал, месяц), вторые — для расчетов развития экономики страны на перспективу. Они отражают процесс воспроизводства в динамике и обеспечивают увязку прогноза производства продукции (услуг) с инвестициями.

Статическая модель МОБ в системе баланса народного хо­зяйства имеет вид

где а_ij — коэффициенты прямых затрат (среднеотраслевые нор­мативы расхода продукции отрасли i, используемой в качестве средств производства для выпуска единицы продукции отрасли j); x_i — объем производства продукции j-й отрасли-потребителя (i = 1,n); X_i — валовое производство продукции (услуг) i-й отрасли-производителя (i = l,n);Y_i — объем конечного продукта i-й отрасли-производителя.

Упрощенная динамическая модель имеет вид

где t — индекс года; I^t_ij— продукция отрасли i, направляемая в качестве производственных инвестиций в t-м году для расши­рения производства в отрасль j; Y^t_i — объем конечного продукта i-и отрасли в t-м году за исключением продукции, направляе­мой на расширение производства.

Сформированный на основе моделей межотраслевой ба­ланс может использоваться для решения многих задач: про­гнозирования макроэкономических показателей, межотрас­левых связей и потоков (поставок), структуры экономики, отраслевых издержек, динамики цен, показателей эффектив­ности производства (материало-, энерго-, металло-, химико- и фондоемкости).

Экономико-статистические модели используются для установления количественной характеристики связи зависи­мости и взаимообусловленности экономических показателей. Система такого рода моделей включает: одно-, многофактор­ные и эконометрические модели.

Примеры однофакторных мо­делей: y = a + bx; y = a + b/x, у = а + b lg_x u др.,

где у- значение прогнозируемого показателя; а - свободный член, определяющий положение начальной точки линии регрессии в системе координат; х - значение фактора, b - пара­метр, характеризующий норму изменения у на единицу х.