Закон распределения дискретной случайной величины
Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причём заранее неизвестно, какое именно.
Случайная величина связана со случайным событием. Если случайное событие – это качественная характеристика испытаний, то случайная величина – его количественная характеристика. Если при этом события независимы, то и соответствующие случайные величины также независимы.
Случайные величины обозначают заглавными буквами латинского алфавита X, Y, Z, их значения – соответствующими строчными буквами.
Случайные величины делятся на два типа: дискретные и непрерывные.
Случайная величина называется дискретной, если все возможные значения изолированы друг от друга и их можно занумеровать.
Случайную величину называют непрерывной, если все её возможные значения заполняют некоторый конечный или бесконечный интервал.
Функция, связывающая значения случайной величины с соответствующими им вероятностями, называется законом распределения дискретной случайной величины. Его чаще всего задают в виде следующей таблицы:
Таблица № 1 Закон распределения
| Значения хi | x1 | x2 | x3 | … | xn |
| Вероятности pi | p1 | p2 | p3 | … | pn |
События xn являются несовместными и единственно возможными, то есть они образуют полную систему событий. Поэтому сумма их вероятностей равна единице.
Пример 1Разыгрываются две вещи стоимостью по 5 рублей и одна вещь стоимостью 30 рублей. Составить закон распределения выигрышей для человека, купившего один билет из 50.
Решение. Искомая случайная величина Х представляет собой выигрыш и может принимать три значения: 0, 5 и 30 рублей. Первому результату благоприятствует 47 случаев, второму результату – 2 случая и третьему – один случай. Найдём их вероятности:
Р(х1) = 47/50 = 0,94, Р(х2) = 2/50 = 0,04, Р(х3) = 1/50 = 0,02.
Закон распределения случайной величины имеет вид
| Значения хi | |||
| Вероятности pi | 0,94 | 0,04 | 0,02 |
В качестве проверки найдём Р(х1) + Р(х2) + Р(х3) = 0,94 + 0,04 + 0,02 = 1
Закон распределения дискретной случайной величины называется биноминальным, если вероятности возможных её значений вычисляются по формуле Бернулли, которая имеет вид:
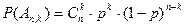 , где (1)
, где (1)
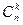 – число сочетаний,
– число сочетаний,
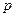 – вероятность наступления события.
– вероятность наступления события.
Пример 2Монету подбрасывают пять раз. Составить закон распределения случайной величины Х – числа выпадения герба.
Решение. Возможны следующие значения случайной величины Х: 0, 1, 2, 3, 4, 5. Зная, что вероятность выпадения герба в одном испытании равна 1/2, найдём вероятности значений случайной величины Х по формуле (1):
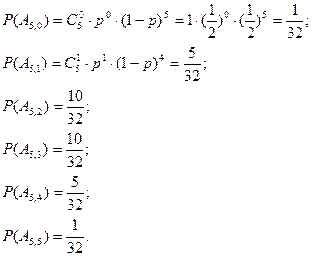
Закон распределения имеет вид
| Значения хi | ||||||
| Вероятности pi | 1/32 | 5/32 | 10/32 | 10/32 | 5/32 | 1/32 |
Произведём проверку: 1/32 + 5/32 + 10/32 + 10/32 + 5/32 + 1/32 = 1.
Пример 3 Монету подбрасывают 10 раз. Какова вероятность, что при этом герб выпадет ровно три раза?
Решение. Пусть А10,3 – событие, состоящее в том, что при десяти кратном подбрасывании монеты герб выпадет три раза. При этом вероятность выпадения герба равна 0,5, то есть р = 0.5. Подставляя эти значения в формулу (1), получим
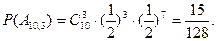
| <== предыдущая лекция | | | следующая лекция ==> |
| Однородные дифференциальные уравнения | | | Представление информации в цифровых устройствах |
Дата добавления: 2017-12-05; просмотров: 988;
