Представление информации в цифровых устройствах
В повседневной жизни мы обычно пользуемся десятичной системой счисления. Это позиционная система счисления, которая имеет 10 арабских цифр от 0 до 9 и, следовательно, основание 10. Т. е. число 6235,89 в десятичной системе счисления представляется выражением
6∙103+2∙102+3∙101+5∙100+8∙10-1+9∙10-2,
или в общем виде
a3∙103+a2∙102+ a1∙101+ a0∙100+ a -1∙10-1+ a -2∙10-2,
где ai, - коэффициенты, принимающие значения 0, 1, 2 … 9.
Цифровые системы оперируют двумя значениями сигнала – логические 0 и 1. Следовательно, для математического представления значений дискретных переменных в цифровых системах используется двоичная система счисления – позиционная система счисления, которая имеет 2 арабских цифры 0 и 1 и, следовательно, основание 2.
Т. е. двоичное число 1001,01 в двоичной системе счисления представляется выражением
1∙23+0∙22+0∙21+1∙20+0∙2-1+1∙2-2 (1.1)
или в общем виде
a3∙23+a2∙22+ a1∙21+ a0∙20+ a -1∙2-1+ a -2∙2-2, (1.2)
где ai, - коэффициенты, принимающие значения 0, 1.
Для определения десятичного эквивалента данного числа достаточно подсчитать сумму произведений в выражении (1.1).
1∙23+0∙22+0∙21+1∙20+0∙2-1+1∙2-2 = 8 + 0 + 0 + 1 + 0 + 0,25 = 9,25
Для перевода числа из десятичной системы счисления в двоичную можно воспользоваться делением десятичного числа на основание 2 и записывать остатки от деления в обратном порядке.
Таблица 1.1 – Перевод двоичного числа в десятичное по степеням двойки
| Двоичное число | ||||||||||
| Степени двойки | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 2-1 | 2-2 |
| 0,5 | 0,25 |
для перевода двоичного числа в десятичное необходимо складывать степени двойки, соответствующие позициям с единичными значениями. В нашем примере
(10101011,11)2.=128 + 32 + 8 + 2 + 1 + 0,5 + 0,25 = (171,75)10.
При работе с цифровыми системами часто приходится иметь дело с восьмиричной и шестнадцатиричной системами счисления. Так как 8 = 23и 16 = 24, каждая восьмиричная цифра соответствует трем бинарным, а каждая шестнадцатиричная цифра соответствует четырем бинарным цифрам. Переход от двоичной к восьмиричной системе счисления выполняется разделением двоичной последовательности на группы из трех цифр (триад), начиная от запятой влево и вправо от нее, и заменой каждой из групп одной восьмиричной цифрой 0, 1, …, 7. Следующий пример иллюстрирует данное правило.
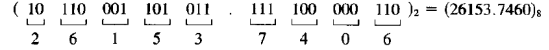
Конвертация двоичного кода в шестнадцатиричный аналогична, за исключением того, что двоичный код разделяется на группы из четырех единиц (тетрады), которые заменяются шестнадцатиричными знаками
0, 1, … , 9, A, B, C, D, E, F.
Следующий пример иллюстрирует данное правило.
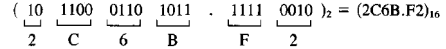
Процедура получения двоичного кода из восьмиричного (шестнадцатиричного) обратна выше упомянутой. Каждая цифра восьмиричного (шестнадцатиричного) кода заменяется на двоичную триаду (тетраду). Это иллюстрирует следующий пример:
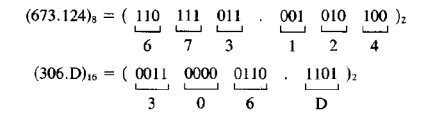
Человеку трудно работать с двоичными числами, потому что они в три, четыре раза длиннее десятичных эквивалентов. Однако цифровые компьютеры используют двоичные числа, а человеку приходится иногда связываться с компьютером посредством бинарных. В этом случае с помощью специальных преобразователей человек может получать двоичную информации в восьмиричном или шестнадцатиричном коде. Подразумевается, что в случае необходимости, пользователь сам перейдет к двоичному коду. Это делается весьма просто и к тому же размер восьмиричного (шестнадцатиричного) кода гораздо меньше двоичного – (111111111111)2 = (7777)8 =(FFF)16 – 3, 4 символа воспринимаются человеком комфортнее, чем 12.
В таблице 1.2. представлены десятичные, двоичные, восьмиричные и шестнадцатиричные коды некоторых чисел.
Таблица 1.2 – Числа различных систем счисления
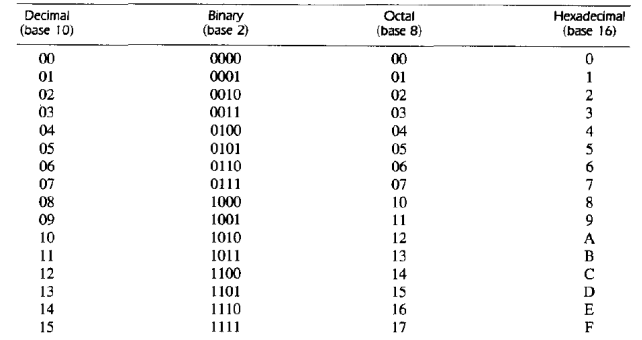
Часто в компьютерных системах используются двоично-десятичные коды (двоичное кодированное представление чисел - BCD (Binary coded decimal)), например в арифметических операциях. Для представления цифры в таком коде необходимо 4 двоичных разряда. В таблице 1.3 приведены примеры некоторых двоично-десятичных кодов десятичных цифр.
1.2 Двоичные сигналы
Бинарные сигналы в современной цифровой технике представляются потенциальным способом, т. е. постоянным напряжением высокого и низкого уровня. Высокий уровень напряжения соответствует логической 1, низкий уровень соответствует логическому 0. Например, определенные цифровые системы могут определят логическую 1 как сигнал с номинальным значением 3 В, а логический 0 как сигнал с номинальным значением 0 В.
2 КОМБИНАЦИОННАЯ ЛОГИКА
2.1 Основы логического синтеза комбинационных схем
2.1.1 Переключательные схемы
Логические функции И (AND), ИЛИ (OR), НЕ (NOT) составляют функционально полный базис, называемый базисом Буля. Он является основой Булевой алгебры. Аппаратные средства, реализующие данные функции называются логическими, вентильными или переключательными элементами (схемами). Функциональная полнота базиса означает возможность описания с помощью него любой логической функции. А логические элементы, реализующие этот базис, позволяют аппаратно реализовывать любую логическую функцию. Рассмотрим Булевы функции и реализующие их элементы.
Элемент И представлен на рис. 2.1. Он реализует операцию конъюнкции или логического умножения.
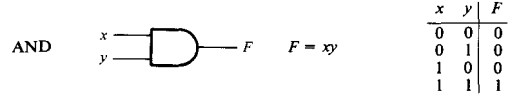
Рисунок 2.1 – Элемент И
Данная функция демонстрируется простым примером электрической цепи (рис. 2.2) с двумя последовательно соединенными механическими переключателями А и В, которые моделируют входные переменные (значения входных сигналов). Разомкнутое состояние переключателей соответствует логическому 0 (не проводит ток), а замкнутое – логической 1 (проводит ток). При подаче двух единиц лампа L будет гореть, что говорит о наличии тока в цепи. Во всех остальных случаях тока в цепи не будет. L моделирует значение функции (значение выходного сигнала). Лампочка горит – логическая 1, не горит – логический 0.
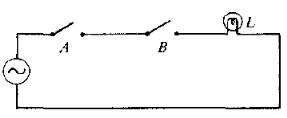
Рисунок 2.2 – Последовательные переключатели, логическое И
Элемент ИЛИ представлен на рис. 2.3. Он реализует операцию дизъюнкции или логического сложения.
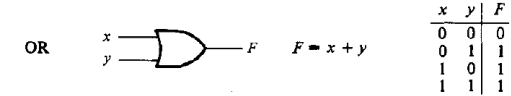
Рисунок 2.3 – Элемент ИЛИ
Данная функция демонстрируется простым примером электрической цепи (рис. 2.4) с двумя параллельно соединенными механическими переключателями А и В. При подаче двух нулей лампа L не будет гореть. Во всех остальных случаях лампа L будет гореть.
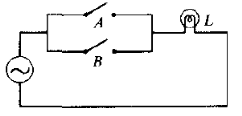
Рисунок 2.4 – Параллельные переключатели, логическое ИЛИ
Элемент НЕ представлен на рис. 2.5. Он реализует операцию отрицания
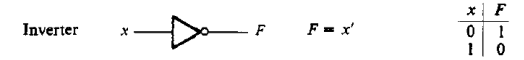
Рисунок 2.5 – Элемент ИЛИ
Временные диаграммы работы данных элементов приведены на рис. 2.6.
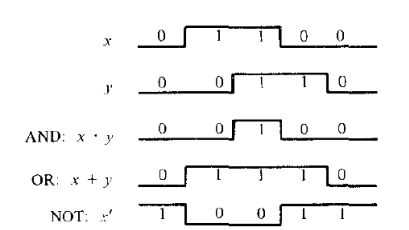
Рисунок 2.6 – Временные диаграммы работы элементов И, ИЛИ, НЕ
Рассматриваемые в данном разделе схемы называются комбинационными.Это схемы, значения выходных сигналов которых зависят только от значений входных сигналов. Это схемы без обратных связей.
На рис. 2.11 представлен буфер. Он реализует операцию повторения. Что поступает на вход такого элемента, то появляется и на его выходе. Элемент используется для усиления сигнала и для управления задержками в схемах.
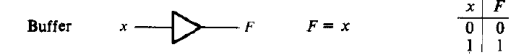
Рисунок 2.11 – Схема буфера
Инвертор и буфер могут использоваться для формирования константных (постоянных) значений 0 и1 (рис.2.12).
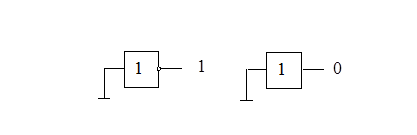
Рисунок 2.12– Схемы реализации константных 0 и1
Элемент И-НЕ (функция Шеффера, образующая функционально полный базис) представлен на рис. 2.1.3.
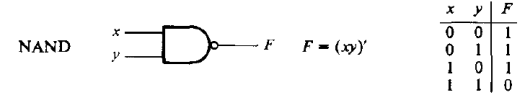
Рисунок 2.13 – Элемент И-НЕ
Рассмотрим некоторые свойства функции Шеффера (2.1).
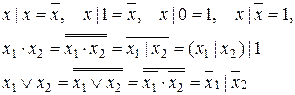 (2.1)
(2.1)
Обратите внимание, что закон коммутативности выполняется, а ассоциативности – нет. Невыполнение ассоциативности проиллюстрируем ниже (выражение 2.2 и рис. 2.14).
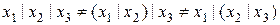 (2.2)
(2.2)
Истинность выражения (2.2) демонстрируется выражениями (2.3).
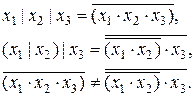 (2.3)
(2.3)
В схемной реализации это проиллюстрировано на рис. 2.14.
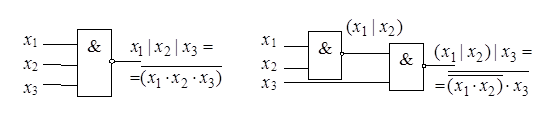
Рисунок 2.14 – Иллюстрация невыполнимости ассоциативности в базисе Шеффера
Для функции И базиса Буля ассоциативность иллюстрируется рис. 2.15. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому.
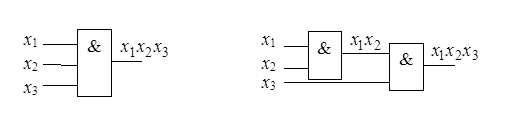
Рисунок 2.15 – Иллюстрация выполнимости ассоциативности в базисе Буля
Рассмотрим переход от базиса Буля к базису Шеффера. Функция в базисе Буля может быть представлена в любой форме, в том числе и в канонической (в виде ДНФ или КНФ). Следующая функция записана в виде ДНФ.
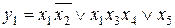
Вне зависимости от представления функции для перехода к базису Шеффера необходимо поставить над выражением двойное отрицание и выполнять преобразования по законам де Моргана.
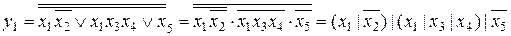
На рис. 2.16 представлена схемная реализация функции 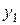 в базисе Буля
в базисе Буля
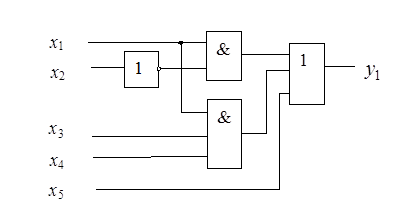
Рисунок 2.16 – Схемная реализация функции 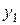 в базисе Буля
в базисе Буля
На рис. 2.17 представлена схемная реализация функции 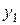 в базисе Шеффера
в базисе Шеффера
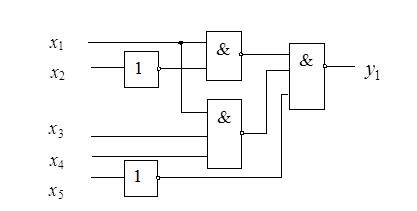
Рисунок 2.17 – Схемная реализация функции 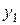 в базисе Шеффера
в базисе Шеффера
Сформулируем правило перехода от ДНФ к уравнению в базисе Шеффера. При переходе от ДНФ к уравнению в базисе Шеффера все термы (элементарные коньюнкции) заключаются в скобки, а все знаки коньюнкций и дизьюнкций заменяются на знак операции Шеффера. Над однобуквенными термами ставятся знаки отрицания.
Элемент ИЛИ-НЕ (функция Пирса (Вебба), образующая функционально полный базис) представлен на рис. 2.1.8.
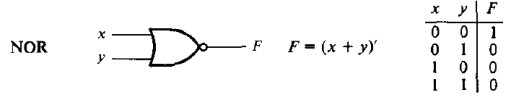
Рисунок 2.18 – Элемент ИЛИ-НЕ
Рассмотрим некоторые свойства функции Шеффера (2.4).
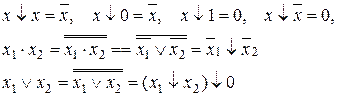 (2.4)
(2.4)
Обратите внимание, что закон коммутативности выполняется, а ассоциативности – нет. Невыполнение ассоциативности проиллюстрируем ниже (выражение 2.5 и рис. 2.19).
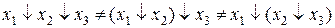 (2.5)
(2.5)
Истинность выражения (2.5) демонстрируется выражениями (2.6).
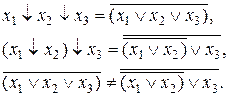 (2.6)
(2.6)
В схемной реализации это проиллюстрировано на рис. 2.19.
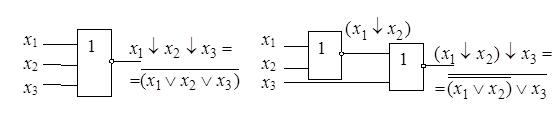
Рисунок 2.19 – Иллюстрация невыполнимости ассоциативности в базисе Пирса
Для функции ИЛИ базиса Буля ассоциативность иллюстрируется рис. 2.20. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому.
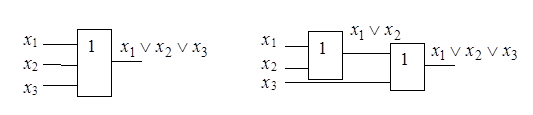
Рисунок 2.20 – Иллюстрация выполнимости ассоциативности в базисе Буля
Рассмотрим переход от базиса Буля к базису Пирса. Функция в базисе Буля может быть представлена в любой форме, в том числе и в канонической (в виде ДНФ или КНФ). Следующая функция записана в виде КНФ.
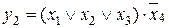
Вне зависимости от представления функции для перехода к базису Пирса необходимо поставить над выражением двойное отрицание и выполнять преобразования по законам де Моргана.
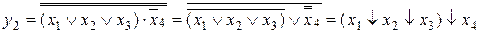
На рис. 2.21 представлена схемная реализация функции 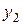 в базисе Буля
в базисе Буля
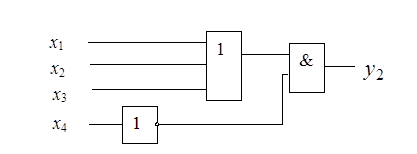
Рисунок 2.21 – Схемная реализация функции 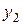 в базисе Буля
в базисе Буля
На рис. 2.22 представлена схемная реализация функции 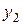 в базисе Пирса
в базисе Пирса
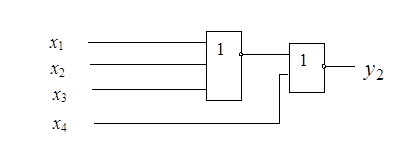
Рисунок 2.22 – Схемная реализация функции 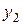 в базисе Пирса
в базисе Пирса
Сформулируем правило перехода от КНФ к уравнению в базисе Пирса. При переходе от КНФ к уравнению в базисе Пирса все термы (элементарные дизьюнкции) заключаются в скобки, а все знаки коньюнкций и дизьюнкций заменяются на знак операции Пирса. Над однобуквенными термами ставятся знаки отрицания.
Рассмотрим переход от ДНФ к базису Пирса на примере функции 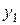 . Для этого необходимо поставить двойные отрицания над всеми термами и над выражением в целом, раскрывая их по правилу де Моргана.
. Для этого необходимо поставить двойные отрицания над всеми термами и над выражением в целом, раскрывая их по правилу де Моргана.
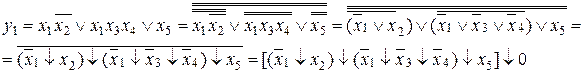
В результате получается менее экономичная с точки зрения аппаратурных затрат реализация, поскольку появляется дополнительная ступень в виде двухвходового элемента, необходимая для реализации инверсии (входные инверсии обычно не учитываются). Это проиллюстрировано на рис. 2.23.
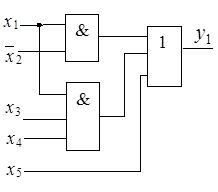
а)
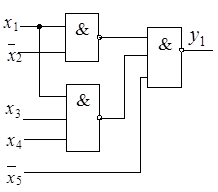
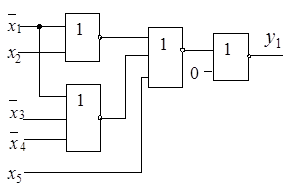
б) в)
Рисунок 2.23 – Схемная реализация функции 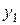 в базисах Буля (а), Шеффера (б) и Пирса (в)
в базисах Буля (а), Шеффера (б) и Пирса (в)
Аналогично выполняется переход от КНФ к Базису Шеффера (выполнить самостоятельно на примере функции 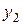 ).
).
Существую еще два стандартных логических вентиля.
Элемент исключающее ИЛИ представлен на рис. 2.24. Он реализует операцию суммы по модулю два.
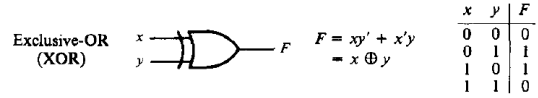
Рисунок 2.24 – Элемент исключающее ИЛИ
Элемент исключающее ИЛИ с инверсией представлен на рис. 2.25. Он реализует операцию отрицания суммы по модулю два (эквивалентность).

Рисунок 2.25 – Элемент эквивалентность
Для функции XOR ассоциативность иллюстрируется рис. 2.26. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому. Справедливость этого высказывания можно проверить, составив две таблицы истинности (выполнить самостоятельно).
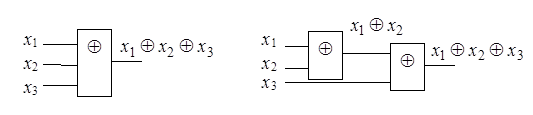
Рисунок 2.26 – Иллюстрация выполнимости ассоциативности XOR
Для функции XNOR ассоциативность не выполняется. Это иллюстрируется рис. 2.27. Каскадное соединение двух двухвходовых вентилей не эквивалентно одному трехвходовому. Справедливость этого высказывания можно проверить, составив две таблицы истинности (выполнить самостоятельно).
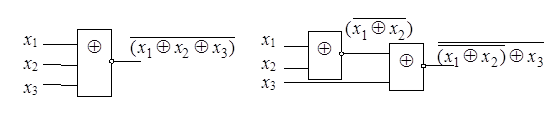
Рисунок 2.27 – Иллюстрация невыполнимости ассоциативности XNOR
На рис. 2.28 приведены временные диаграммы последних четырех рассмотренных стандартных логических элементов.
Рисунок 2.28 – Временные диаграммы
2.1.2 Интегральные схемы
Цифровые схемы конструируются на базе интегральных схем (ИС). ИС – маленькие полупроводниковые кристаллы, называемые «чипами» (chip). Вентили, реализуемые электронными компонентами, соединены в ИС определенным способом, образуя заданную схему. Кристаллы устанавливаются в керамические или пластиковые корпуса и подсоединяются к внешним выводам корпуса (pins). Число выводов (ножек) микросхем может быть различным: 8, 14, 16, …, 64 и более. Размер микросхем достаточно мал. Например микросхема, содержащая 4 двухвходовых вентиля И, имеет 14 выводов и корпус размером 20×8×3 мм. А процессор с 64 выводами упаковывается в корпус размером 50×15×4 мм. Выводы микросхем бывают различных типов: в виде ножек, контактных площадок, штырьков или контактных шариков. На поверхности каждой микросхемы наносится маркировка для ее идентификации. В специальной справочной литературе можно найти информацию о микросхеме по ее маркировке.
ИС часто классифицируются в соответствии со сложностью, измеряемой числом вентилей, упакованных в одном корпусе. ИС могут содержать несколько, десятки, сотни, тысячи и сотни тысяч вентилей. В связи с этим существует следующее разделение ИС по группам.
ИС малой степени интеграции (МИС) – Small-scale integration (SSI) содержит несколько независимых вентилей, упакованных в одном корпусе. Входы и выходы вентилей связаны непосредственно с выводами микросхемы. Количество выводов обычно немногим более 10.
ИС средней степени интеграции (СИС) – Medium-sale integration (MSI) содержит от 10 до 100 вентилей в одном корпусе. Они обычно выполняю специфические элементарные операции, такие как операции декодеров, мультиплексоров, сумматоров. Это могут быть также триггеры, регистры, счетчики.
ИС большой степени интеграции (БИС) – Large-scale integration (LSI) содержат от 100 до нескольких тысяч вентилей. Это процессоры, микроконтроллеры, микросхемы памяти, программируемые логические устройства.
ИС сверх большой степени интеграции (СБИС) – Very large-scale integration (VLSI) содержат от тысяч до сотен тысяч вентилей. Это большие матрицы памяти, системы на кристаллах. Благодаря маленьким размерам и низкой стоимости, СБИС схемы совершили революцию в технологии проектирования компьютерных систем.
2.1.3 Позитивная и негативная логика
До сих пор мы рассматривали позитивную логику, когда высокому уровню напряжения H соответствует логическая 1, низкому уровню напряжения L соответствует логический 0. Использование низкого уровня L для представления логической 1, а высокого уровня H для представления логического 0 определяет негативную логику (рис. 2.39).
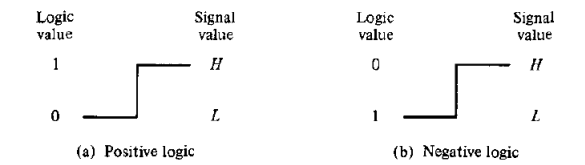
Рисунок 2.39 – Негативная и позитивная логика
Термин позитивная и негативная логика несколько обманчивы, поскольку оба сигнала могут быть позитивными или негативными
Далее мы не будем более касаться негативной логики и будем все рассматривать с точки зрения позитивной логики.
Описание физического поведения вентиля, когда H=3.5 В, а L=0 В. Таблица истинности этого вентиля предполагает позитивную логику, т.е Н=1, L=0. Очевидно, что это вентиль И (рис. 2.41).
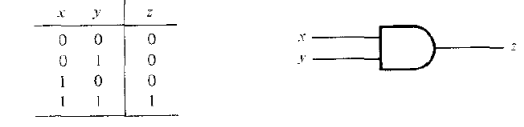
Рисунок 2.41 – ТТЛ вентиль И позитивной логики
Для перехода к негативной логике (т.е Н=0, L=1) вентиля (рис. 2.40), необходимо заменить в таблице истинности 0 на 1, 1 на 0, а функцию на двойственную ей (в данном случае это функция ИЛИ). Т.е. такой вентиль интерпретируется как вентиль И в позитивной логике или как вентиль ИЛИ в негативной (рис. 2.42).
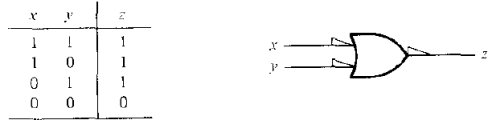
Рисунок 2.42 – ТТЛ вентиль ИЛИ негативной логики
Маленькие треугольники на входах и выходах вентиля говорит о том, что подразумевается негативная логика.
2.2 Минимизация Булевых функций
2.2.1 Минимизация Булевых функций методом карт Карно
Под минимизацией будем понимать процесс нахождения такого эквивалентного выражения функции алгебры логики, которое содержит минимальное число вхождений переменных (букв в выражении). Хотя, в общем случае, под минимизацией может иметься в виду получение выражений с минимальным числом инверсных переменных либо с минимальным числом вхождений какой-либо одной переменной и т.п.. Большинство методов минимизации ориентированы на получение МДНФ (МКНФ), однако доказано, что минимальное выражение в классе ДНФ будет либо минимальным, либо отличаться от минимального на какое- то число вхождений переменной в классе других форм функции.
Приведем некоторые определения.
Элементарное произведение - произведение любого числа букв (переменных), взятых с отрицанием или без.
ДНФ (дизъюнктивная нормальная форма) - дизъюнкция элементарных произведений.
Минтерм (конституэнта 1) - произведение всех переменных, взятых с отрицанием или без, на которых функция принимает значение 1.
СДНФ (совершенная ДНФ) - дизъюнкция всех минтермов.
Импликанта - элементарное произведение, которое покрывает по крайней мере один из минтермов булевой функции, но не приводит к новым (ненужным) каноническим суммам элементарных произведений.
Другое определение импликанты.
Импликантой называется элементарное произведение, равное 1 на одном или нескольких наборах, где данная функция равна 1, и равное 0 на всех наборах, где данная функция равна 0. Импликанта покрывает один или несколько минтермов рассматриваемой булевой функции. Обычно, импликанта - это результат склеивания соответствующих минтермов или импликант.
Простая импликанта - импликанта, которая содержит минтерм функции, но перестает быть импликантой после удаления любого аргумента (иными словами, это импликанта, к которой не нельзя применить операцию склеивания).
Сокращенная ДНФ - дизъюнкция всех простых импликант.
Существенная импликанта - простая импликанта, образованная склеиванием таких минтермов, что по крайней мере для одного из них эта операция была единственной
Существенные импликанты образуют ядро функции.
Тупиковая ДНФ - дизъюнкция простых импликант, из которых ни одна не является лишней.
Кратчайшая ДНФ - тупиковая ДНФ, имеющая минимальное число простых импликант.
МДНФ (минимальная ДНФ) - тупиковая ДНФ с минимальным числом вхождений переменных (минимальным числом букв) по сравнению с другими тупиковыми формами этой функции.
Элементарная сумма, КНФ, макстерм (конституэнта 0), СКНФ, имплицента, простая имплицента, сокращенная КНФ, существенная имплицента, тупиковая КНФ, кратчайшая КНФ, МКНФ определяется аналогично.
Элементарная сумма - дизъюнкция любого числа букв (переменных), взятых с отрицанием или без.
КНФ (конъюнктивная нормальная форма) - конъюнкция элементарных дизъюнкций.
Макстерм (конституэнта 0) - дизъюнкция всех переменных, взятых с отрицанием или без, на которых функция принимает значение 0.
СКНФ (совершенная КНФ) - конъюнкция всех макстермов.
Имплицента – результат склеивания макстермов или имплицент.
Рассмотрим визуальный метод минимизации булевых функций с помощью карт (диаграмм) Карно, который является одним из наиболее удобных методов при небольшом числе переменных (до 6). Данный метод был разработан в 1953 г. американским ученым Морисом Карно.
Карта Карно является координатным способом представления булевых функций. Карта Карно – развертка на плоскости n-мерного единичного куба. Т.е. клетки карты соответствуют координатам куба.
На рис. 2.49 приведены примеры одномерного, двумерного и трехмерного единичных кубов, представляющих различные булевы функции одной, двух и трех переменных соответственно. Кубы называются единичными, поскольку их ребра соединяют вершины, наборы которых отличаются на единицу. В вершинах кубов записываются значения функции, соответствующие наборам.
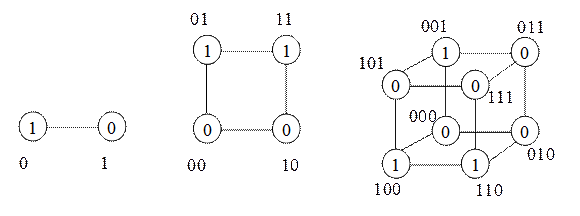
Рисунок 2.49 – Примеры одномерного, двумерного и трехмерного единичных кубов
При задании функции Картой Карно таблица истинности функции представляется в виде координатной карты состояний, которая содержит 2n клеток (по числу входных наборов булевой функции n переменных). Переменные функции разбиваются на две группы так, что одна группа определяет координаты столбца карты, а другая - координаты строки. При таком способе построения каждая клетка определяется значениями переменных, соответствующих определенному двоичному набору. Внутри каждой клетки карты Карно ставится значение функции на данном наборе. Переменные в строках и столбцах располагаются так, чтобы соседние клетки карты Карно различались только в одном разряде переменных, т.е. были соседними. Поэтому значения переменных в столбцах и в строках карты образуют соседний код Грея. Такой способ представления очень удобен для наглядности при минимизации булевых функций. Карта Карно 4 переменных, с точки зрения определения «соседства» переменных, геометрически представляет собой пространственную фигуру тор или, проще говоря, «бублик».
Отметим, что метод карт Карно применим к минимизации булевых функций до 6-ти переменных (до 4 переменных на плоскости) и до 6 - в трехмерной интерпретации.
На рис 2.51 представлены карты Карно для двух, трех и четырех переменных. В каждой ячейке карты синим цветом показан номер соответствующего двоичного набора в десятичном эквиваленте.
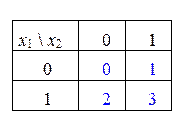
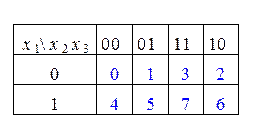
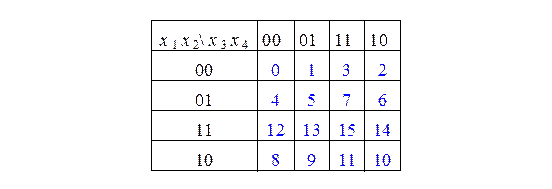
Рисунок 2.51 – Примеры Карт Карно
Дата добавления: 2017-12-05; просмотров: 3034;
