Однородные дифференциальные уравнения
Определение 8.Дифференциальное уравнение вида, которое можно привести к виду 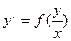 , называется однородным.
, называется однородным.
Для интегрирования таких уравнений производят замену переменных, полагая 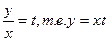 . Эта подстановка приводит к дифференциальному уравнению относительно x и t, в котором переменные разделяются, после чего уравнение можно интегрировать. Для получения окончательного ответа надо переменную t заменить на
. Эта подстановка приводит к дифференциальному уравнению относительно x и t, в котором переменные разделяются, после чего уравнение можно интегрировать. Для получения окончательного ответа надо переменную t заменить на 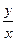 .
.
Например,решить уравнение 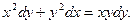
Решение. Перепишем уравнение так:
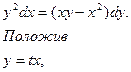
получим: 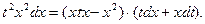
После сокращения на х2 имеем:
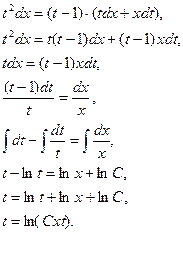
Заменим t на 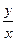 :
:
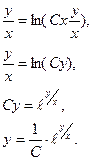
Вопросы для повторения
1 Какое уравнение называется дифференциальным?
2 Назовите виды дифференциальных уравнений.
3 Рассказать алгоритмы решения всех названных уравнений.
Пример 3
Решить дифференциальное уравнение 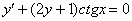
Решение: Переписываем производную в нужном нам виде:
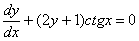
Оцениваем, можно ли разделить переменные? Можно. Переносим второе слагаемое в правую часть со сменой знака:
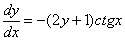
И перекидываем множители по правилу пропорции:
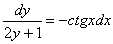
Переменные разделены, интегрируем обе части:
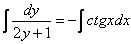
Должен предупредить, приближается судный день. Если вы плохо изучили неопределенные интегралы, прорешали мало примеров, то деваться некуда – придется их осваивать сейчас.
Интеграл левой части легко найти методом подведения функции под знак дифференциала, с интегралом от котангенса расправляемся стандартным приемом, который мы рассматривали на уроке Интегрирование тригонометрических функций в прошлом году:
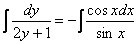
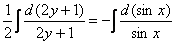
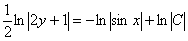
В правой части у нас получился логарифм, согласно моей первой технической рекомендации, в этом случае константу тоже следует записать под логарифмом.
Теперь пробуем упростить общий интеграл. Поскольку у нас одни логарифмы, то от них вполне можно (и нужно) избавиться. Максимально «упаковываем» логарифмы. Упаковка проводится с помощью трёх свойств:
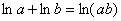
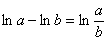
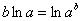
Пожалуйста, перепишите эти три формулы к себе в рабочую тетрадь, при решении диффуров они применяются очень часто.
Решение распишу очень подробно:
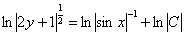
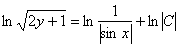
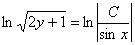
Упаковка завершена, убираем логарифмы:
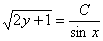
Можно ли выразить «игрек»? Можно. Надо возвести в квадрат обе части. Но делать этого не нужно.
Третий технический совет: Если для получения общего решения нужно возводить в степень или извлекать корни, то в большинстве случаев следует воздержаться от этих действий и оставить ответ в виде общего интеграла. Дело в том, что общее решение будет смотреться вычурно и ужасно – с большими корнями, знаками  .
.
Поэтому ответ запишем в виде общего интеграла. Хорошим тоном считается представить общий интеграл в виде 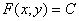 , то есть, в правой части, по возможности, оставить только константу. Делать это не обязательно, но всегда же выгодно порадовать профессора ;-)
, то есть, в правой части, по возможности, оставить только константу. Делать это не обязательно, но всегда же выгодно порадовать профессора ;-)
Ответ: общий интеграл: 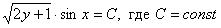
Примечание:общий интеграл любого уравнения можно записать не единственным способом. Таким образом, если у вас не совпал результат с заранее известным ответом, то это еще не значит, что вы неправильно решили уравнение.
Общий интеграл тоже проверяется довольно легко, главное, уметь находить производные от функции, заданной неявно. Дифференцируем ответ:
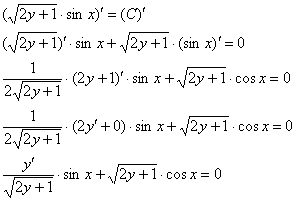
Умножаем оба слагаемых на 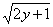 :
:
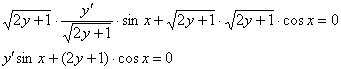
И делим на 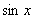 :
:
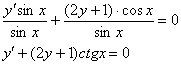
Получено в точности исходное дифференциальное уравнение 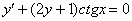 , значит, общий интеграл найден правильно.
, значит, общий интеграл найден правильно.
Пример 4
Найти частное решение дифференциального уравнения 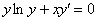 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 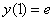 . Выполнить проверку.
. Выполнить проверку.
Это пример для самостоятельного решения. Напоминаю, что задача Коши состоит из двух этапов:
1) Нахождение общего решение.
2) Нахождение частного решения.
Проверка тоже проводится в два этапа (см. также образец Примера 2), нужно:
1) Убедиться, что найденное частное решение действительно удовлетворяет начальному условию.
2) Проверить, что частное решение вообще удовлетворяет дифференциальному уравнению.
Полное решение и ответ в конце урока.
Пример 5
Найти частное решение дифференциального уравнения 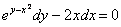 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 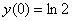 . Выполнить проверку.
. Выполнить проверку.
Решение:Сначала найдем общее решение.Данное уравнение уже содержит готовые дифференциалы 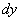 и
и 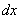 , а значит, решение упрощается. Разделяем переменные:
, а значит, решение упрощается. Разделяем переменные:

Интегрируем уравнение:
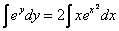
Интеграл слева – табличный, интеграл справа – берем методом подведения функции под знак дифференциала:
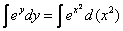
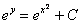
Общий интеграл получен, нельзя ли удачно выразить общее решение? Можно. Навешиваем логарифмы:
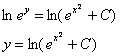
(Надеюсь, всем понятно преобразование 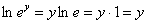 , такие вещи надо бы уже знать)
, такие вещи надо бы уже знать)
Итак, общее решение:
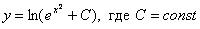
Найдем частное решение, соответствующее заданному начальному условию 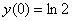 . В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
. В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
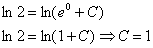
Более привычное оформление: 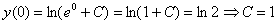
Подставляем найденное значение константы 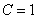 в общее решение.
в общее решение.
Ответ: частное решение: 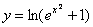
Проверка: Сначала проверим, выполнено ли начальное условие 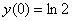 :
:
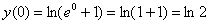 – всё гуд.
– всё гуд.
Теперь проверим, а удовлетворяет ли вообще найденное частное решение 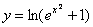 дифференциальному уравнению. Находим производную:
дифференциальному уравнению. Находим производную:
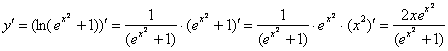
Смотрим на исходное уравнение: 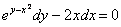 – оно представлено в дифференциалах. Есть два способа проверки. Можно из найденной производной выразить дифференциал
– оно представлено в дифференциалах. Есть два способа проверки. Можно из найденной производной выразить дифференциал 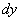 :
:
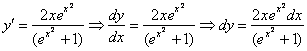
Подставим найденное частное решение 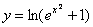 и полученный дифференциал
и полученный дифференциал  в исходное уравнение
в исходное уравнение 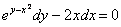 :
:

Используем основное логарифмическое тождество 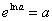 :
:

Получено верное равенство, значит, частное решение найдено правильно.
Второй способ проверки зеркален и более привычен: из уравнения 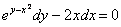 выразим производную, для этого разделим все штуки на
выразим производную, для этого разделим все штуки на 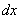 :
:

И в преобразованное ДУ подставим полученное частное решение 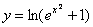 и найденную производную
и найденную производную  . В результате упрощений тоже должно получиться верное равенство.
. В результате упрощений тоже должно получиться верное равенство.
Пример 6
Решить дифференциальное уравнение 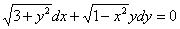 . Ответ представить в виде общего интеграла
. Ответ представить в виде общего интеграла 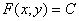 .
.
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Какие трудности подстерегают при решении дифференциальных уравнений с разделяющимися переменными?
1) Не всегда очевидно (особенно, чайнику), что переменные можно разделить. Рассмотрим условный пример: 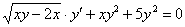 . Здесь нужно провести вынесение множителей за скобки:
. Здесь нужно провести вынесение множителей за скобки: 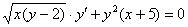 и отделить корни:
и отделить корни: 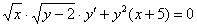 . Как действовать дальше – понятно.
. Как действовать дальше – понятно.
2) Сложности при самом интегрировании. Интегралы нередко возникают не самые простые, и если есть изъяны в навыках нахождения неопределенного интеграла, то со многими диффурами придется туго. К тому же у составителей сборников и методичек популярна логика «раз уж дифференциальное уравнение является простым, то пусть интегралы будут посложнее».
3) Преобразования с константой. Как все заметили, с константой в дифференциальных уравнениях можно делать практически всё, что угодно. И не всегда такие преобразования понятны новичку. Рассмотрим еще один условный пример: 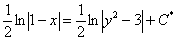 . В нём целесообразно умножить все слагаемые на 2:
. В нём целесообразно умножить все слагаемые на 2: 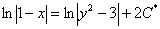 . Полученная константа
. Полученная константа 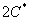 – это тоже какая-то константа, которую можно обозначить через
– это тоже какая-то константа, которую можно обозначить через 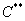 :
: 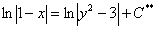 . Да, и коль скоро в правой части логарифм, то константу
. Да, и коль скоро в правой части логарифм, то константу 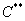 целесообразно переписать в виде другой константы:
целесообразно переписать в виде другой константы: 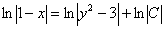 .
.
Беда же состоит в том, что частенько не заморачиваются с индексами, и используют одну и ту же букву 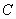 . И в результате запись решения принимает следующий вид:
. И в результате запись решения принимает следующий вид:
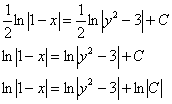
Что за фигня? Тут же ошибки. Формально – да. А неформально – ошибки нет, подразумевается, что при преобразовании константы 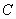 всё равно получается какая-то другая константа
всё равно получается какая-то другая константа 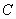 .
.
Или такой пример, предположим, что в ходе решения уравнения получен общий интеграл 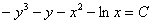 . Такой ответ выглядит некрасиво, поэтому целесообразно сменить у всех множителей знаки:
. Такой ответ выглядит некрасиво, поэтому целесообразно сменить у всех множителей знаки: 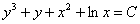 . Формально по записи тут опять ошибка, следовало бы записать
. Формально по записи тут опять ошибка, следовало бы записать 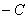 . Но неформально подразумевается, что
. Но неформально подразумевается, что 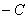 – это всё равно какая-то другая константа (тем более
– это всё равно какая-то другая константа (тем более 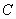 может принимать любое значение), поэтому смена у константы знака не имеет никакого смысла и можно использовать одну и ту же букву
может принимать любое значение), поэтому смена у константы знака не имеет никакого смысла и можно использовать одну и ту же букву 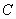 .
.
Я буду стараться избегать небрежного подхода, и всё-таки проставлять у констант разные индексы при их преобразовании.
Пример 7
Решить дифференциальное уравнение 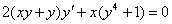 . Выполнить проверку.
. Выполнить проверку.
Решение: Данное уравнение допускает разделение переменных. Разделяем переменные:
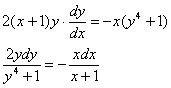
Интегрируем:
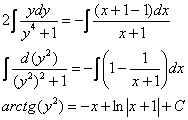
Константу 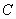 тут не обязательно определять под логарифм, поскольку ничего путного из этого не получится.
тут не обязательно определять под логарифм, поскольку ничего путного из этого не получится.
Ответ: общий интеграл: 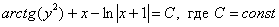
Проверка: Дифференцируем ответ (неявную функцию):
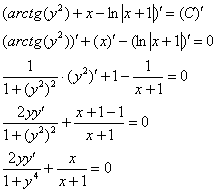
Избавляемся от дробей, для этого умножаем оба слагаемых на 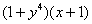 :
:
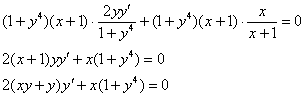
Получено исходное дифференциальное уравнение, значит, общий интеграл найден правильно.
Пример 8
Найти частное решение ДУ.
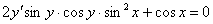 ,
, 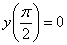
Это пример для самостоятельного решения. Единственный комментарий, здесь получится общий интеграл, и, правильнее говоря, нужно исхитриться найти не частное решение, ачастный интеграл. Полное решение и ответ в конце урока.
Как уже отмечалось, в диффурах с разделяющимися переменными нередко вырисовываются не самые простые интегралы. И вот еще парочка таких примеров для самостоятельного решения. Рекомендую всем прорешать примеры №№9-10, независимо от уровня подготовки, это позволит актуализировать навыки нахождения интегралов или восполнить пробелы в знаниях.
Пример 9
Решить дифференциальное уравнение 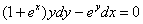
Пример 10
Решить дифференциальное уравнение 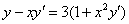
Помните, что общий интеграл можно записать не единственным способом, и внешний вид ваших ответов может отличаться от внешнего вида моих ответов. Краткий ход решения и ответы в конце урока.
Следующая рекомендуемая статья – Однородные дифференциальные уравнения первого порядка.
Успешного продвижения!
Решения и ответы:
Пример 4:Решение:Найдем общее решение. Разделяем переменные:
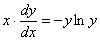
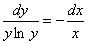
Интегрируем:
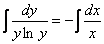
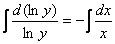
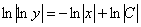
Общий интеграл получен, пытаемся его упростить. Упаковываем логарифмы и избавляемся от них:
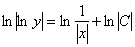
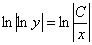
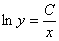
Выражаем функцию в явном виде, используя 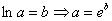 .
.
Общее решение: 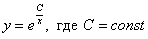
Найдем частное решение, удовлетворяющее начальному условию 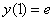 .
.
Способ первый, вместо «икса» подставляем 1, вместо «игрека» – «е»:
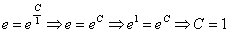 .
.
Способ второй:
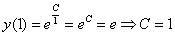
Подставляем найденное значение константы 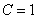 в общее решение.
в общее решение.
Ответ:частное решение: 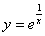
Проверка: Проверяем, действительно ли выполняется начальное условие:
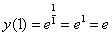 , да, начальное условие
, да, начальное условие 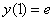 выполнено.
выполнено.
Проверяем, удовлетворяет ли вообще частное решение 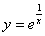 дифференциальному уравнению. Сначала находим производную:
дифференциальному уравнению. Сначала находим производную:
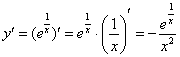
Подставим полученное частное решение 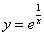 и найденную производную
и найденную производную 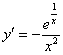 в исходное уравнение
в исходное уравнение 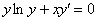 :
:
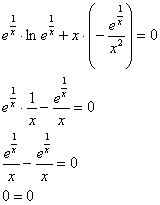
Получено верное равенство, значит, решение найдено правильно.
Пример 6:Решение:Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
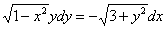
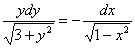
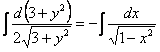
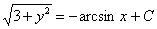
Ответ:общий интеграл: 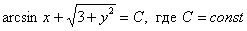
Примечание: тут можно получить и общее решение:
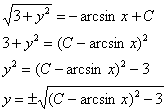
Но, согласно моему третьему техническому совету, делать это нежелательно, поскольку такой ответ смотрится довольно хреново.
Пример 8:Решение:Данное ДУ допускает разделение переменных. Разделяем переменные:
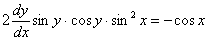
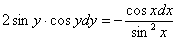
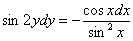
Интегрируем:
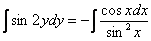
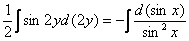
Общий интеграл: 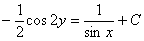
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию 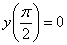 . Подставляем в общее решение
. Подставляем в общее решение 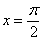 и
и 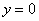 :
:
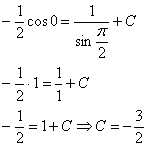
Ответ:Частный интеграл: 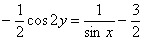
В принципе, ответ можно попричесывать и получить что-нибудь более компактное.
Пример 9:Решение:Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
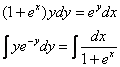
Левую часть интегрируем по частям:

В интеграле правой части проведем замену:
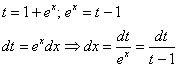
Таким образом:
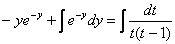
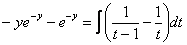
(здесь дробь раскладываетсяметодом неопределенных коэффициентов, но она настолько простая, что подбор коэффициентов можно выполнить и устно)
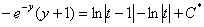
Обратная замена: 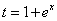
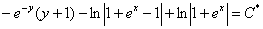
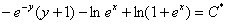
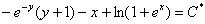
Ответ:общий интеграл: 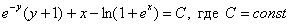
Пример 10:Решение:Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
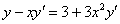
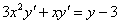
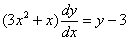
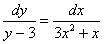
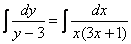
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
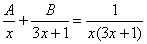
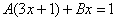
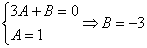
Примечание: Интеграл 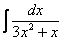 можно было также найти методом выделения полного квадрата.
можно было также найти методом выделения полного квадрата.
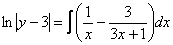

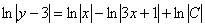
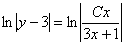
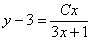
Ответ:общее решение: 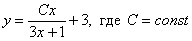
 Примеры: 1.
Примеры: 1. 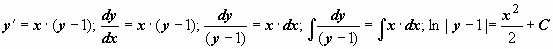 .
.
 При такой форме записи общего интеграла решение y = 1 потеряно. Можно преобразовать общее решение к виду, который содержит это решение. Переобозначим постояннуюC как ln|C1|:
При такой форме записи общего интеграла решение y = 1 потеряно. Можно преобразовать общее решение к виду, который содержит это решение. Переобозначим постояннуюC как ln|C1|: 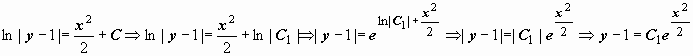 . Вернёмся к обозначению постоянной интегрирования C; общее решение
. Вернёмся к обозначению постоянной интегрирования C; общее решение 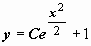 содержит частное решение y = 1 при C = 0.
содержит частное решение y = 1 при C = 0.
 2. Найти решение задачи Коши
2. Найти решение задачи Коши 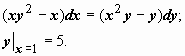
Решаем уравнение: 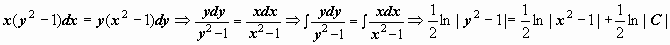 . Здесь могут быть потеряны решения
. Здесь могут быть потеряны решения 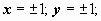 постоянная интегрирования записана как
постоянная интегрирования записана как 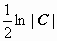 . Далее,
. Далее, 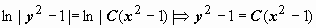 . Общий интеграл уравнения
. Общий интеграл уравнения
y2 = C(x2 – 1) + 1. Частные решения 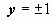 содержатся в общем интеграле при C = 0, решения
содержатся в общем интеграле при C = 0, решения 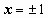 утеряны (понятно, почему это произошло: если записать уравнение в форме, решённой относительно производной,
утеряны (понятно, почему это произошло: если записать уравнение в форме, решённой относительно производной, 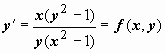 , то, очевидно, на решениях
, то, очевидно, на решениях 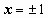 нарушаются условия, налагаемые теоремой Коши на правую часть уравнения). Всё множество решений: y2 = C(x2 – 1) + 1, x = 1, x = -1. Мы должны найти ещё частное решение, удовлетворяющее начальному условию y(1) = 5. Подстановка значений x = 1, y = 5 в общий интеграл даёт 25=1, т.е. общий интеграл этого частного решения не содержит. Решение x = 1 удовлетворяет начальному условию, это и есть решение задачи Коши.
нарушаются условия, налагаемые теоремой Коши на правую часть уравнения). Всё множество решений: y2 = C(x2 – 1) + 1, x = 1, x = -1. Мы должны найти ещё частное решение, удовлетворяющее начальному условию y(1) = 5. Подстановка значений x = 1, y = 5 в общий интеграл даёт 25=1, т.е. общий интеграл этого частного решения не содержит. Решение x = 1 удовлетворяет начальному условию, это и есть решение задачи Коши.
 К уравнениям с разделяющимися переменными сводятся уравнения вида
К уравнениям с разделяющимися переменными сводятся уравнения вида 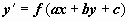 (
( 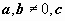 - постоянные). Если перейти к новой неизвестной функции z = ax + by+ c, то
- постоянные). Если перейти к новой неизвестной функции z = ax + by+ c, то 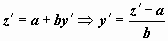 , и уравнение представляется как
, и уравнение представляется как 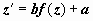 . Это - уравнение с разделяющимися переменными.
. Это - уравнение с разделяющимися переменными.
 Пример:
Пример: 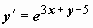 .
. 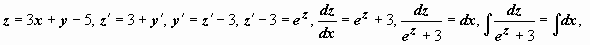
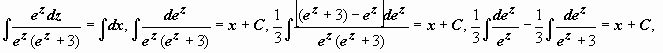
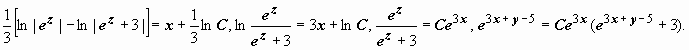
Дата добавления: 2017-12-05; просмотров: 3552;
