Найти производную функции и вычислить y’( .

Решение.

y’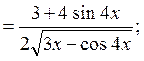

.

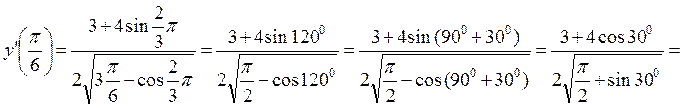
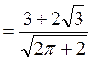№ 5 Исследуйте функцию 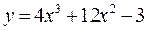на экстремум.

Решение.

Найдем производную, приравняем ее к нулю и решим полученное уравнение:

y’=12x²+24х

12х²+24х=0

12х(х+2)=0

х=0 или х=-2

Воспользуемся достаточными признаками экстремума и проверим меняет ли знак первая производная при переходе через критические точки от меньших значений к большим. Здесь первая производная существует при любых значениях x. Оценим знаки производной при x=3, x=-1, x=1

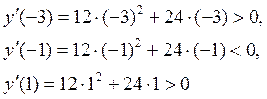
Итак, при переходе слева направо через критическую точку x=-2производная меняет знак с “+” на “–“, то есть функция слева возрастает, а справа убывает. Значит, x=-2 – точка максимума функции. Найдем ее ординату в этой точке:

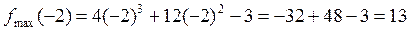
При переходе слева направо через критическую точку x=0 производная меняет знак с “+” на “-”, следовательно, слева убывает справа возрастает, то есть для нее x=0 – точка минимума, причем .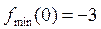

Экстремумы данной функции:

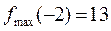
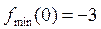
№ 6 Найдите наибольшее и наименьшее значения функции y=x²-x³ на отрезке [-1;3].

Решение.

Исследуем функцию на экстремум. Если точки экстремума принадлежат данному отрезку, то вычисляем значения функции в точках экстремума и на концах отрезка и выбираем из них наибольшее и наименьшее

y’=2x-3x²;

2x-3x²=0; x(2-3x)=0

х₁=0; x₂= 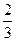– критические точки, причем обе принадлежат отрезку [-1;3]. Вычислим значения функции:

f(0)=0, f(-1)=2, f(3)=-18, f(2/3)=4/27

Ответ:f_наиб.=2, f_наим.= -18.

№ 7 Найдите вторую производную функции 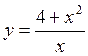и вычислите f’’(4).

Решение.

Найдем первую производную, дифференцируя данную функцию как частное:

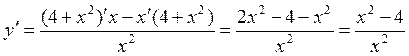
теперь найдем вторую производную аналогично:

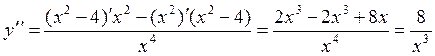
Вычислим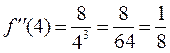

Ответ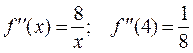

№ 8 Тело движется прямолинейно по закону s(t)=3t³-4t+2. Найти скорость и ускорение в момент времени t=3.

Решение.

Если известен закон движения как функция времени, то скорость и ускорение – это соответственно первая и вторая производные по времени, то есть

v=s’(t)=9t²-4, тогда v _t=3=s’(3)=9*3²-4=77 м/с.

а= s’’(t)=18t, a_t=3=s’’(3)=18*3=54 м/с².

№ 9 Найдите точки перегиба графика функции .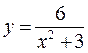

Решение.

Для нахождения точек перегиба надо найти вторую производную данной функции, приравнять ее к нулю и решить полученное уравнение. Корни этого уравнения – это критические точки второго рода или точки возможного перегиба. Найдем первую производную

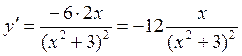
теперь найдем вторую производную

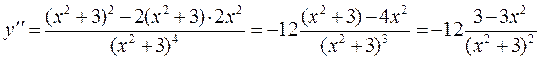
приравнивая вторую производную к нулю, получим уравнение

3-3x²=0

1-x²=0

откуда x_1,2= ±1 – критические точки второго рода

Проверим, действительно ли точки x= ±1 являются точками перегиба. Поскольку для данной функции:

,

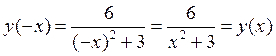то функция четная, значит, если x=1 – точка перегиба, то x= -1 – тоже точка перегиба. Проверим, меняет ли знак вторая производная при переходе через точку x=1. Возьмем, например, x= 0 (-1<0<1) и подставим во вторую производную. Получим 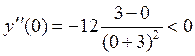. Возьмем теперь x=2, (2>1), тогда 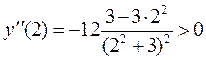, (вычислять не обязательно, достаточно правильно оценить знак). Поскольку вторая производная меняет знак при переходе через точку x=1, то эта точка есть точка перегиба, но тогда и точка x=-1 – тоже точка перегиба. Ордината обеих точек перегиба будет 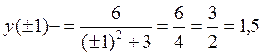, поскольку точки перегиба лежат на самой кривой. Итак, точки N₁(-1;1,5), N₂(1;1,5) – точки перегиба графика данной функции

N₁(-1;1,5), N₂(1;1,5) – точки перегиба

№ 10 Постройте график функции .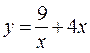

Решение.

Эскизное построение графика можно выполнить по общепринятой в анализе схеме.

1 Найдем область определения функции: x ε(-∞,0) U (0, ∞); x = 0 – точка бесконечного разрыва, а прямая x = 0 – вертикальная асимптота кривой.

2 Исследуем функцию на четность (нечетность). Вместо x положим (–x). Получим:

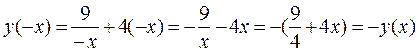, а это признак нечетности функции. Следовательно, ее график центрально симметричен относительно начала координат. Поэтому его можно построить для положительных x и симметрично относительно начала координат перенести для отрицательных x.

3 Найдем точки пересечения графика с осями координат, так называемые “нули” функции. Здесь x≠0 , т.к. x=0 не входит в область определения, значит, с осью O y график не пересекается. Пусть y=0, тогда 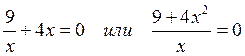. Это равенство невозможно, так как 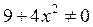при любых значения x. Значит, с осью O y график тоже не пересекается.

4 Найдем точки экстремума и нанесем их на график.

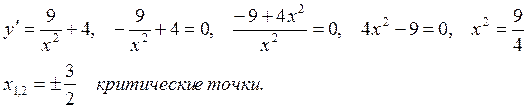
Исследуем характер экстремума в точке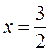

Оценим знаки производной при x=1 и x=2:

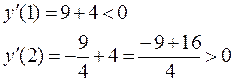, таким образом 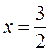– абсцисса точки минимума.

Найдем ординату минимума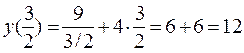

Итак, 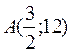– точка минимума.

Но тогда, в силу центральной симметрии, точка 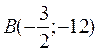– точка максимума.

5 Интервалы монотонности функции:

функция возрастает, если ;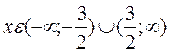

функция убывает, если .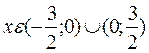

6 Найдем точки перегиба и интервалы выпуклости и вогнутости графика функции 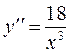и ни при каких значениях x вторая производная не обращается в нуль, а в точке разрыва x=0 функция не определена. Следовательно, график не имеет точек перегиба.

Поскольку при x>0 y’’>0 , то для x ε(0;∞) кривая вогнутая, а для x ε(-∞;0) (в силу симметрии) – выпуклая.

7 По итогам исследования строим график функции y= :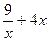

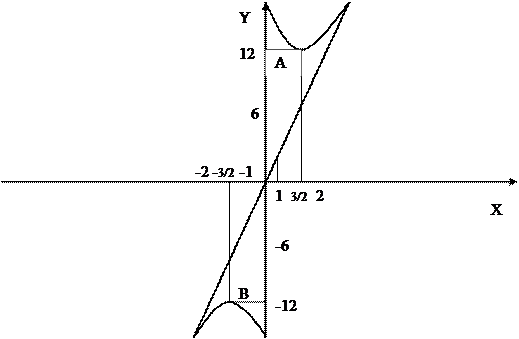
Рисунок 1 График функции y=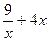

№11 Вычислить приближенное значение функции y=x³-3x²+30 при изменении аргумента от 3 до 3,002.

Решение.

При небольших изменениях аргумента (здесь приращение аргумента ∆x=3,002-3=0,002 небольшое) можно воспользоваться формулой приближенного значения функции f(x₀+∆x)≈f(x₀)+f’(x₀) ∆x.

Примем f(x)=y=x³-3x²+30, тогда f’(x)=3x²-6x, положим x₀=3, ∆x=0,002.

Вычислим f(x)=3³-3∙3²+30=30; f’(3)=3∙3²-6∙3=9. Тогда, по формуле будем иметь f(3,002) ≈30+9∙0,002=30+0,018=30,018.