Непрерывность функции

Ещё одним важным свойством является свойство непрерывности функции.

Рассмотрим примеры. Поставили кипятить воду. С течением времени температура воды повышается. Но как? Постепенно, то есть за малый промежуток времени, температура повысится незначительно.

Аналогично, небольшим промежуткам времени отвечают малые изменения температуры воздуха.

Наглядное представление о непрерывной функции состоит в том, что график такой функции можно начертить одним непрерывным движением, не отрывая карандаша от бумаги. На рисунке 1 изображена некоторая непрерывная функция.

Функция f(x) называется непрерывной в точке х = х₀, если:

1 эта функция определена в точке х = х₀ (то есть определённому значению аргумента х, равному х₀, соответствует вполне определённое значение функции y, равное y₀);

2 приращение функции в точке х₀ стремится к нулю при 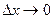, то есть

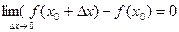(8)

Геометрически непрерывность функции означает, что ординаты двух точек графика сколь угодно мало отличаются друг от друга, если достаточно мало отличаются их абсциссы. Часто пользуются другим определением непрерывности функции в точке.

Функция f(x) называется непрерывной в данной точке х₀, если её предел в точке х₀ существует и равен значению функции в этой точке.

Функция называется непрерывной на отрезке 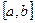, если она непрерывна в каждой точке этого отрезка.

Исследуем на непрерывность функцию .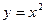

Решение. Пусть приращение аргумента х равно Δх, тогда функция y получит какое-то приращение Δy. Имеем

,

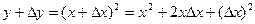откуда

.

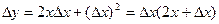Очевидно, что при любом фиксированном значении х и при Δх, стремящемся к нулю, Δy также стремится к нулю, то есть функция 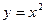непрерывна при любом значении х.