Предел функции в точке

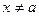2.1. Число А называется пределом функции f(x) при , если для любого числа ε>0 можно указать такое δ>0, что для любого , удовлетворяющего неравенству 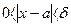, выполняется неравенство 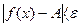. В этом случае пишут .

Если число А₁ (число А₂) есть предел функции y = f(x) при x, стремящемся к a так, что х принимает только значения, меньшие (большие) а, то А₁ (А₂) называется левым (правым) пределом функции f(x) в точке а. При этом соответственно пишут .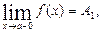

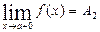2.2. Постоянная величина b называется пределом функции ƒ(x) при x стремящемся к x₀ (x→ x₀), если для всех x сколь угодно мало отличающихся от x₀ соответствующие значения функции ƒ(x) сколь угодно мало отличаются от b. То есть, при x→ x₀ , ƒ (x) →b, .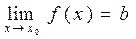

Замечание:

x может стремится не только к конечному x₀ , но и к бесконечности (x → ∞), и к нулю (x→0).

Функция f(x) называется бесконечно малой при , если .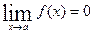

Функция f(x) называется бесконечно большой при , если .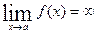

Теоремы о пределах

1 Если функция y= ƒ(x) имеет предел при x→0, то этот предел единственный.

2 Предел постоянной величины равен этой же постоянной , независимо от того, к чему стремится переменная.

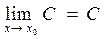, где С= const (1)

3 Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен алгебраической сумме пределов всех слагаемых.

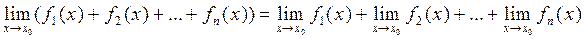(2)

3 Предел произведения конечного числа функций, имеющих конечные пределы, равен произведению пределов сомножителей.

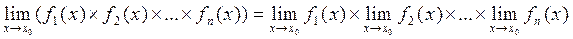(3)

4 Предел частного двух функций, имеющих пределы, равен отношению пределов числителя и знаменателя, если предел знаменателя не равен нулю.

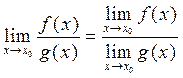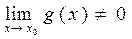, где (4)

5 Постоянный множитель можно выносить за знак предела:

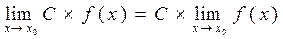, где С= const (5)