Вычисление пределов

Рассмотрим некоторые примеры вычисления пределов функций.

№ 1 Вычислить пределы:

a) ;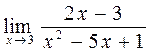

б) ;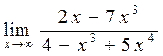

в) ;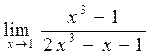

г) .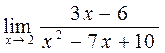

Решение

а) Пользуясь теоремами о пределах, получим

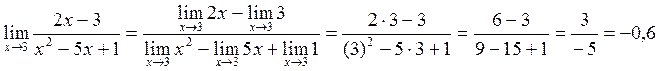
б)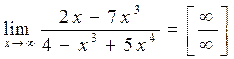

Для того чтобы раскрыть неопределенность 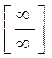в данном пределе поделим почленно числитель и знаменатель на x в старшей степени в данном выражении, т.е. на x⁴ . Получим

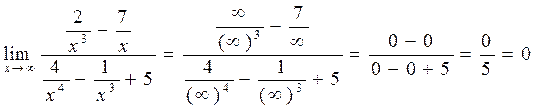
в) Применяя теоремы о пределах, обнаруживаем, что 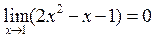, то есть, знаменатель дроби обращается в нуль. Значит, теорему о пределах дроби здесь пока применить нельзя. Но поскольку и предел числителя 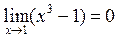, то для того, чтобы раскрыть получившуюся 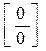неопределенность, мы разложим числитель и знаменатель на множители

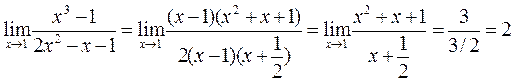
Сокращение дроби на (x-1)здесь возможно, поскольку x→1 , но x ≠ 1и множители (x-1) в нуль не обращаются, а являются эквивалентными бесконечно малыми величинами при x→1, отношения которых равно единице

г) 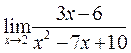. Если воспользоваться теоремами о пределах и подставить x = 2 в правую часть вместо x, то получим неопределенность 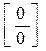. Неопределенность можно устранить, если выделить и сократить эквивалентные бесконечно малые в числителе и знаменателе. Разложим знаменатель на множители, а в числителе вынесем за скобку 3. Получим

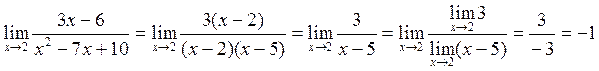
Здесь дробь можно сократить на x-2, так как x→2, но x≠2.