Переход от естественных обозначений к более компактным.

Многие данные, несущие информацию о каких-либо объектах, как правило, имеют вид, удобный для их чтения человеком. При этом они содержат обычно больше символов, чем это необходимо для адекватного восприятия передаваемой с их помощью информации. Наличие такой избыточности позволяет перекодировать информацию более компактно, поступаясь наглядностью ее представления в интересах эффективности передачи по каналу связи.

Например, дата записывается обычно в виде «26 сентября 2007 г.» (18 символов, включая пробелы) или в более краткой форме «26.09.07». При анализе смыслового содержания выясняется, что информацию о дате можно кодировать и шестью десятичными разрядами, если договориться, что первые два разряда несут информацию о числе, следующие два разряда – о месяце и последние два – о годе даты (существование американского формата даты, когда первыми идут две цифры месяца, доказывает, что вводимые соглашения вовсе не так очевидны, как это кажется на первый взгляд). В этом случае рассматриваемую дату можно будет записать в виде «260907» - еще менее наглядно, но зато более компактно.

Для посимвольного двоичного кодирования даты потребуется 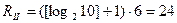бита (в формуле 4.2 n=10, т.к. A={0,1,…,9}, и L^S_max=6).

Однако, легко заметить, что многие кодовые комбинации – такие, как 331853 или 950011 – вообще никогда не используются и рассматриваемый способ кодирования является избыточным.

Вычислим количество возможных кодовых комбинаций (а, значит, и число m возможных сообщений о дате). Поскольку

ЧИСЛО = {01, 02, … , 31};

МЕСЯЦ = {01, 02, … , 12};

ГОД = {00, 01, … , 99},

то m ≤ 31∙12∙100 = 37200 и по формуле 1.1

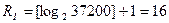бит, т.е. при кодировании сообщений целиком нам потребуется 16 двоичных разрядов, что на 33,3% экономнее, чем при посимвольном кодировании.

Здесь следует отметить, что на практике было бы более удобно, хотя, теоретически, и не так экономно, кодировать число, месяц и год в отдельности, выделив для этого соответствующее количество разрядов, и затем объединить полученные коды в единое двоичное кодовое слово. При этом формула 1.1 примет вид

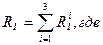
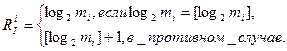
С учетом того, что m₁=31, m₂=12, m₃=100 получим

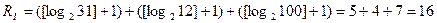бит.

Однако и этот способ кодирования не оптимален. Допустим, при анализе выясняется, что нас будут интересовать даты не от 1 января 2000 г. по 31 декабря 2099 г., а из более узкого диапазона, например, от 1 января 2007 г. по 17 сентября 2096 г. В этом случае можно еще больше сжать данные и кодировать информацию о дате не шестью, а пятью десятичными разрядами. Для этого применим способ, известный еще в средние века: записывать общее число дней, прошедших до некоторой даты от выбранной точки отсчета (начала диапазона), в нашем случае – от 1 января 2007 г. Так как от этой даты до 17 сентября 2096 г. прошло 32768 дней, то становится понятно, почему для кодирования потребуется пять десятичных разрядов. Получим ли мы выигрыш при двоичном кодировании дат в указанном диапазоне? Да, т.к. 32768=2¹⁵ и 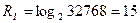бит.

Обратим внимание, что при раздельном кодировании числа, месяца и года дат этого диапазона выигрыша мы бы не получили:

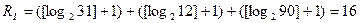бит.

Также экономия отсутствовала бы, если бы нас интересовали даты из более широкого диапазона, скажем, с 1 января 2006 г.: в этом случае количество дат в диапазоне до 17.09.96 превысило бы 2¹⁵ дней и R_I=16 бит.

Аналогично датам могут быть сжаты номера изделий, уличные адреса и т.п.