Процедура Шеннона-Фано

В этом алгоритме предварительно производится упорядочивание сообщений по возрастанию или убыванию вероятностей p_j. Разбиение на подмножества производится путем выбора разделяющей границы в упорядоченной последовательности так, чтобы суммарные вероятности подмножеств были по возможности одинаковыми. Кодовое дерево, построенное этим методом для примера в таблице 1.1, приведено на рис.1.5. Возле каждой вершины дерева указывается суммарная вероятность соответствующего подмножества.

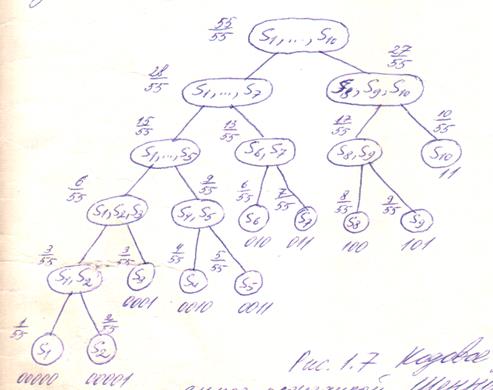
Рис.1.5

Кодовое дерево в процедуре Шеннона-Фано

Выполнив расчеты по формуле 1.3, получим: λ_k^S=3,145(бит/сообщение).Таким образом, код, полученный при помощи процедуры Шеннона-Фано, оказывается более экономным, чем код из таблицы 1.1.

Процедура Хафмана

Рассмотренная в §13процедура Шеннона-Фано является простым, но не всегда оптимальным алгоритмом построения экономного кода. Причина состоит в том, что способ разбиения на подмножества ограничен: вероятности сообщений, отнесенных к первому подмножеству, всегда больше или всегда меньше вероятностей сообщений, отнесенных ко второму подмножеству. Оптимальный алгоритм, очевидно, должен учитывать все возможные комбинации при разбиении на равновероятные подмножества. Это обеспечивается в процедуре Хафмана.

Процедура Хафмана представляет собой рекурсивный алгоритм, который строит бинарное дерево «в обратную сторону», т.е. от конечных вершин к корню. Основная идея алгоритма состоит в том, чтобы объединить два сообщения с наименьшими вероятностями – например, p₁ и p₂ – в одно множество и далее решать задачу с m-1 сообщениями и вероятностями p₁’ = p₁ + p₂; p₂’ = p₃; … ; p_{m-1’ =} p_m. Кодовое дерево, построенное процедурой Хафмана для рассматриваемого примера, приведено на рис.1.6.

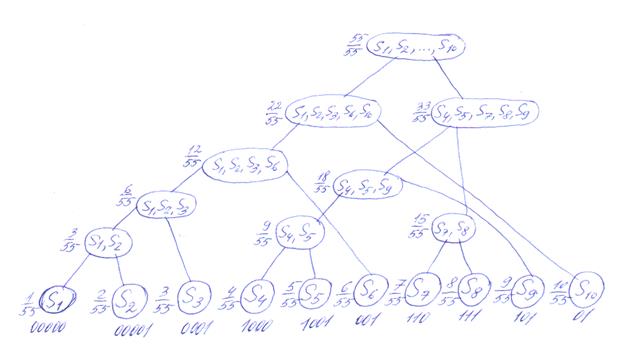
Рис.1.6

Кодовое дерево в процедуре Хафмана

Расчеты по формуле 1.3 дают среднее значение длины кодового слова λ_k^S=3,145(бит/сообщение), что совпадает с результатом применения процедуры Шеннона-Фано. Это означает, что для данного примера процедура Шеннона-Фано также оказалась оптимальной.