Сжатие на основе статистических свойств данных и неравномерные коды

Методы такого сжатия изучаются в специальном разделе теории информации (подразделе теоретической информатики), который называется теорией экономного или эффективного кодирования. Экономное кодирование основано на использовании систем кодирования с переменной длиной кодового слова.

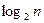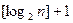В системах равномерного кодирования, как нам уже известно, каждому символу алфавита A={a_i}, i=1,…,n,ставится в соответствие кодовое слово с фиксированным числом разрядов. Например, в случае рассмотренного нами посимвольного двоичного кодирования каждому знаку алфавита A соответствует или бит (двоичных разрядов). Однако давно известны и системы кодирования, в которых длина кодового слова непостоянна, например, код Морзе.

При использовании таких неравномерных кодов сразу же возникает проблема выделения кодовых слов из закодированной последовательности символов для однозначного декодирования сообщений. Например, в коде Морзе для этого предусмотрена специальная кодовая комбинация-разделитель (тройная пауза). Однако более экономным является использование при кодировании так называемого условия префиксности кода (условия Фано): никакое кодовое слово не должно являться началом другого кодового слова. Выполнение этого условия гарантирует однозначное разбиение последовательности символов на кодовые слова без применения разделителей: очередное кодовое слово получается последовательным считыванием символов до тех пор, пока получающаяся комбинация не совпадет с одним из кодовых слов.

Пусть, например, A={0,1, … ,9}. Закодируем символы данного алфавита наборами двоичных знаков следующим образом:

0 – 00 5 – 110

1 ­– 01 6 – 1110

2 – 1000 7 – 11110

3 – 1001 8 – 111110

4 – 101 9 – 111111

Нетрудно видеть, что перед нами – префиксный код. Теперь появляется возможность однозначного декодирования любого сообщения. Например, последовательность 1110110111110100000000110011111110101 допускает лишь одно разбиение на кодовые слова 1110 110 111110 1000 00 00 01 1001 111111 01 01 и соответствует сообщению 65820013911.

Префиксный код называется примитивным, если его нельзя сократить, т.е. при вычеркивании любого знака хотя бы в одном кодовом слове код перестает быть префиксным. Префиксный код, приведенный выше в качестве примера, является примитивным.