РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
СТАТИСТИЧЕСКИХ ДАННЫХ
Ряды распределения
Результаты сводки и группировки данных статистического наблюдения оформляются в виде статистических рядов распределения и таблиц.
Статистические ряды распределения– это упорядоченное расположение единиц изучаемой совокупности или групп по группировочному признаку. Они характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности, границах её изменения, закономерностях наблюдаемого объекта.
Ряды распределения, построенные по качественному признаку, называют атрибутивными. Например, распределение работников по занимаемой должности, профессии, образованию; распределение предприятий по форме собственности, виду основной деятельности и другим качественным признакам.
При группировке ряда по количественному признаку образуются вариационныеряды. Вариационные ряды по способу построения бывают дискретными (прерывными), построенными на прерывной вариации признака (число человек в семье, касс в магазине, комнат в квартире), и интервальными (непрерывными), базирующимися на непрерывно изменяющемся значении признака, имеющем любые (в том числе и дробные) количественные выражения (объём товарооборота, величина фонда оплаты труда, выработка рабочего). При построении интервальных рядов распределения возникают вопросы о числе групп, величине интервала, его границах.
Вариационные ряды состоят из двух элементов: варианты и частоты.
Варианта –это отдельное значение варьируещего признака, которое он принимает в ряду распределения.
Частотаминазываются численности отдельных вариант или численности единиц каждой группы вариационного ряда. Частоты, выраженные в долях единицы или в процентах к итогу называются частостями. Сумма частот составляет объём ряда распределения.
Статистический ряд распределения по атрибутивному признаку представлен в табл.12.
Табл.12. Распределение продавцов магазина по категориям
| Группа продавцов по категориям (атрибутивный признак) | Число продавцов, чел. (частота) | В % к итогу (частость) |
| Первая Вторая Третья |
Итого: 200 100
Если группировку в виде ряда распределения продавцов по категориям составить за два периода по данному магазину, то можно выявить происходящие структурные изменения (в данном случае – качественные сдвиги) в составе категории работников.
Дискретные вариационные ряды распределения магазинов района по числу секций на две даты представлены в табл.13.
В приведенных в табл.13 рядах частоты выражены в процентах, что позволяет посредством их сравнения обнаружить процесс увеличения количества товарных секций в магазинах на начало 2003г. по сравнению с началом 2000г. Это во многом связано со складывающейся конъюнктурой рынка, вызвавшей расширение ассортимента товаров и приведшей к разукрупнению существующих и созданию новых товарных секций.
Табл.13. Распределение магазинов района по числу товарных секций
| Число товарных секций | На 1 января 2000 г. | На 1 января 2003 г. | ||
| Число магазинов | В % к итогу | Число магазинов | В % к итогу | |
Итого: 60 100 75 100
В статистических вариационных рядах существует определённая связь между частотами и значениями варьирующего признака: с увеличением признака величина частот вначале возрастает до определённой величины, а затем уменьшается.
Такие изменения называют закономерностями распределения. Для характеристики закономерностей распределения вариационных рядов в статистике часто используют известные в математике законы распределения, примерами которых могут служить:
-нормальное распределение
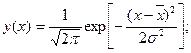
- распределение Пуассона
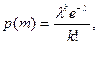
где 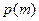 - вероятность появления события с частотой
- вероятность появления события с частотой 
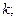
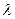 - среднее число появления события в одинаковых независимых испытаниях;
- среднее число появления события в одинаковых независимых испытаниях; 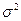 - дисперсия;
- дисперсия; 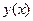 - вес или частота значения признака х.
- вес или частота значения признака х.
В реальных статистических исследованиях социально-экономических процессов и явлений чаще всего закон распределения варьирующего признака в вариационных рядах неизвестен. В таких случаях для характеристики рядов распределений рассчитывают начальные и центральные моментыи связанные с ними показатели.
Начальные моментыk-го порядка определяются по формулам

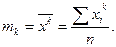
При 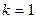 имеем начальный момент
имеем начальный момент 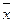 - среднее значение признака; при
- среднее значение признака; при 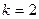 имеем начальный момент второго порядка
имеем начальный момент второго порядка 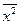 - средний квадрат значений признака и т.д.
- средний квадрат значений признака и т.д.
Центральные моменты 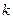 -го порядка определяют по формулам
-го порядка определяют по формулам
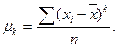
При 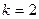 имеем центральный момент второго порядка
имеем центральный момент второго порядка 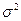 - дисперсию варьирующего признака.
- дисперсию варьирующего признака.
На практике чаще всего исчисляют следующие основные характеристики распределения:
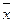 - среднее значение варианты (математическое ожидание);
- среднее значение варианты (математическое ожидание);
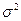 - дисперсия;
- дисперсия;
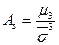 - коэффициент асимметрии;
- коэффициент асимметрии;
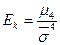 - эксцесс и др.,
- эксцесс и др.,
которые достаточно точно выявляют форму распределения и весовое содержание варьирующего признака в нём.
В математике доказывается теорема о том, что знание бесконечного числа моментов распределения эквивалентно полному знанию о распределении вариационного ряда.
Дата добавления: 2017-11-04; просмотров: 1102;
