Графическое изображение вариационного ряда

Графическое изображение дискретного вариационного ряда производится с помощью построения полигона.

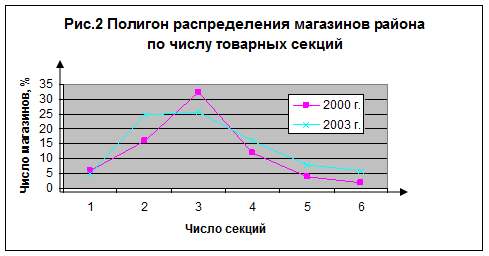
Характер рядов распределения, представленных в табл.13, проиллюстрирован графически в виде полигона распределения на рис.2. Рисунок подтверждает сделанные выше (по данным табл.13) выводы.

Графическое изображение интервального вариационного ряда распределения проводится с помощью построения гистограммы и графика кумуляты(накопленной частоты) распределения.

Рассмотрим интервальный ряд распределения по данным табл.14.

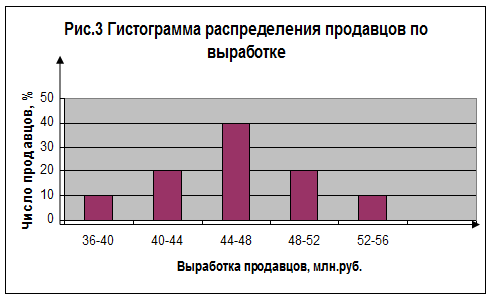
Интервальный ряд распределения изображается графически в виде гистограммы следующим образом. На оси абсцисс откладывают интервалы ряда. Над интервалами по оси абсцисс строят прямоугольники, высота которых равна соответствующим частотам или частостям. Данные табл.14 представлены на рис.3.

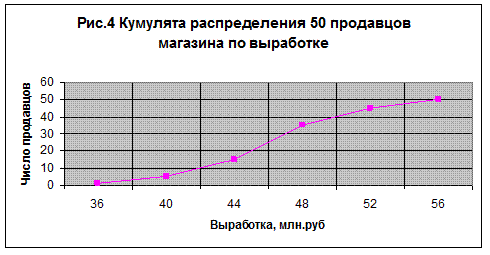
Иногда в практике экономической работы возникает необходимость в преобразовании рядов распределения в кумулятивные ряды, строящиеся по накопленным частотам или частостям. С их помощью можно прослеживать за процессом концентрации изучаемого явления. Например, в табл.14 накопленная частота первых трёх групп показывает число продавцов с размером выработки в диапазоне 36-48 млн. руб. (35 продавцов).

Табл.14. Распределение продавцов магазина по выработке

Итого 50 100

Накопленные частоты определяются путём последовательного прибавления к частотам (или частотям) первой группы этих показателей последующих групп ряда. Используя данные накопленного ряда, строят график в виде кумуляты. На рис.4 представлена кумулята по данным табл.14.

Иногда частоты в вариационных рядах с неравными интервалами не сопоставимы. В этих случаях для обеспечения необходимой сравнимости исчисляют и строят графически функцию плотности распределения,определяющую, сколько единиц каждой группы приходится на единицу величины интервала.