Средние величины, их сущность и их виды
В процессе обработки и обобщения статистических данных существует необходимость определения средних величин. Каждая однородная статистическая совокупность состоит из достаточно большого числа единиц, которые отличаются размерами количественных признаков. Вместе с тем, каждая единица совокупности по определению несет черты, свойственные всей совокупности. Расчёт средних величин позволяет выявить типичный уровень признаков и черт изучаемой совокупности.
Средними величинаминазываются обобщающие показатели, характеризующие типичный уровень варьирующего признака в расчёте на единицу совокупности в конкретных условиях места и времени.
Правильное понимание сущности средней величины определяет её особую значимость в условиях рыночной экономики, когда среднее через единичное и случайное позволяет выявить общее и необходимое, выявить тенденцию закономерностей экономического развития. В условиях реальной экономической, в том числе коммерческой, деятельности постоянные причины (факторы ) действуют одинаково на каждое изучаемое явление и именно они делают эти явления похожими друг на друга и создают общие для всех закономерности. Результатом учения об общих и индивидуальных причинах явлений стало выделение средних величин в качестве основного приёма статистического анализа, базирующегося на утверждении, что статистические средние величины представляют собой не просто меру математического измерения, а категорию объективной действительности. В статистической теории типическая реально существующая средняя величина отожествляется с истинной для данной совокупности величиной, отклонения от которой могут быть только случайными.
Например, выработка продавца зависит от многих причин: квалификации, стажа, возраста, формы обслуживания, воспитания, здоровья и т.д. А средняя выработка (продажа) на одного продавца отражает общее типичное свойство всей совокупности продавцов. Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством.
Таким образом, средние величины – обобщающие показатели, в которых находит выражение действие общих условий, закономерность изучаемого явления.
В практике статистической обработки данных возникают различные задачи, имеются особенности изучаемых явлений, и поэтому для их решения требуются различные средние.
По уровню обобществления данных изучаемой совокупности средние могут быть общими и групповыми. Средняя, рассчитанная по совокупности в целом, называется общей средней,а средние, исчисленные для каждой группы, - групповыми средними.
Различают степенные и структурные средние.
Степенные средние выводятся из общей формулы вида:
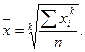
С изменением показателя степени 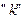 приходим к определенному виду средней:
приходим к определенному виду средней:
при 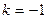 - средняя гармоническая;
- средняя гармоническая;
при 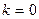 - средняя геометрическая;
- средняя геометрическая;
при 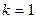 - средняя арифметическая;
- средняя арифметическая;
при 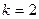 - средняя квадратическая.
- средняя квадратическая.
Вопрос о том, какой вид средней необходимо применять в отдельном случае, решается путём конкретного анализа изучаемой совокупности, материальным содержанием изучаемого явления, осмыслением результатов осреднения. Только тогда средняя величина применена правильно, когда в результате осреднения получают величины, имеющие реальный смысл.
Вводятся следующие обозначения:
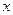 – количественный признак, по которому находится средняя, называется осредняемым признаком;
– количественный признак, по которому находится средняя, называется осредняемым признаком;

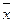 – среднее значениепризнака (с чертой сверху), представляющее результат осреднения;
– среднее значениепризнака (с чертой сверху), представляющее результат осреднения;
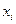 - индивидуальные значения признака у единиц совокупности
- индивидуальные значения признака у единиц совокупности 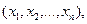 называемые вариантами;
называемые вариантами;
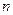 – общее число единиц совокупности;
– общее число единиц совокупности;
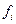 - частота или повторяемость индивидуального значения признака
- частота или повторяемость индивидуального значения признака 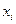 (его вес);
(его вес);
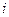 - усредняющий признак (индекс).
- усредняющий признак (индекс).
В зависимости от наличия исходных данных средние можно рассчитать различным образом. В случае, если индивидуальные значения осредняемого признака (варианты) не повторяются при конкретных значениях усредняющего признака 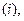 применяются формулы простых степенных средних.Однако, когда в практических исследованиях отдельные значения изучаемого признака
применяются формулы простых степенных средних.Однако, когда в практических исследованиях отдельные значения изучаемого признака 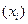 встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторения индивидуальных значений признака (
встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторения индивидуальных значений признака ( 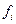 - вес признака) присутствует в формулах степенных средних. В этом случае они называются формулами взвешенных степенных средних. В формулах взвешенных средних вместо частот
- вес признака) присутствует в формулах степенных средних. В этом случае они называются формулами взвешенных степенных средних. В формулах взвешенных средних вместо частот 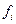 может содержаться частость
может содержаться частость

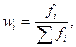
определяемая как отношение частоты признака к сумме частот.
В табл.9 приведены формулы расчёта различных видов степенных простых и взвешенных средних величин.
Табл.9. Формулы расчёта степенных средних величин
Значение
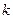
| Название средней | Формула средней | |
| простая | взвешенная | ||
| - 1 | Средняя гармоническая | 
| 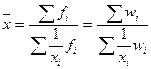
|
| Средняя геометрическая |
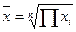
|
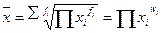
| |
| Средняя арифметическая |
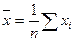
|

| |
| Средняя квадратическая |
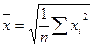
|
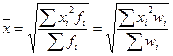
|
Средняя арифметическая – наиболее распространённый вид средней. Она исчисляется в случаях, когда объём осредняемого признака образуется как сумма его значений у отдельных единиц совокупности. Например, требуется вычислить средний стаж десяти работников предприятия, причём дан ряд одиночных значений признака 6, 5, 4, 3, 3, 4, 5, 4, 5, 4. Тогда объём осредняемого признака
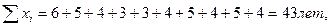
а среднее значение вычисляется по формуле простой средней 
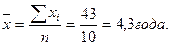
Если те же данные сгруппированы по величине признака, то среднее значение вычисляется по формуле взвешенной средней
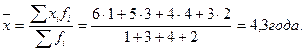
Средняя гармоническая величина чаще всего вычисляется, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а имеются данные по объёмам осредняемого признака, относящимся к отдельным вариантам совокупности. Например, необходимо вычислить среднюю цену единицы товара, причём даны объёмы реализации по каждому виду товара 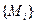
 в виде ряда 600, 1000, 850 (тыс. руб.) и соответствующие цены по каждому виду товара
в виде ряда 600, 1000, 850 (тыс. руб.) и соответствующие цены по каждому виду товара 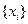 в виде ряда 20, 40, 50 (тыс. руб./шт.). Тогда средняя цена вычисляется по формуле средней гармонической взвешенной
в виде ряда 20, 40, 50 (тыс. руб./шт.). Тогда средняя цена вычисляется по формуле средней гармонической взвешенной
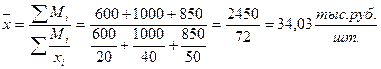
Можно видеть, что средняя гармоническая является превращённой (обратной) формой средней арифметической. Вместо средней гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса 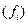 отдельных значений признака.
отдельных значений признака.
При использовании формулы средней геометрической индивидуальные значения признака, как правило, представляют собой относительные величины динамики, построенные в виде цепных величин (как отношения последующих уровней показателя к предыдущим уровням в ряду динамики), причём временные отрезки ряда динамики одинаковы (сутки, месяц, год). Средняя геометрическая величина характеризует, таким образом, средний коэффициент роста. Например, для данных ряда динамики, представленных в табл.10,
Табл.10. Ряд динамики роста доходов населения
Год 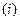
| (базовый) | |||
Отношение доходов последующего периода к предыдущему 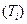
| 1,04 | 1,144 | 1,35 |
средний темп роста доходов населения вычисляется по формуле средней геометрической простой
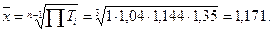
Формула средней квадратической величины используется для измерения средней степени колеблемости значений признака около среднего арифметического значения в рядах распределения. Так, например, при расчёте такого показателя вариации, как дисперсия, среднюю вычисляют из квадратов отклонений индивидуальных значений признака от средней арифметической величины (см. в главе 6).
Степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения, причём чем больше показатель степени 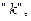 тем больше и величина соответствующей средней
тем больше и величина соответствующей средней
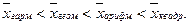
Это свойство степенных средних называется мажорантностью средних.
Для характеристики структуры совокупности применяются особые показатели, которые называют структурнымисредними. К таким показателям относятся мода и медиана.
Модой 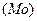 называется наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака.
называется наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака.
Например, выборочное обследование 8 пунктов обмена валюты позволило зафиксировать различные цены за доллар (табл.11). В этом случае модальной ценой за доллар является величина 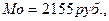 поскольку в обследованной совокупности пунктов обмена валюты она встречается наиболее часто ( 3 раза).
поскольку в обследованной совокупности пунктов обмена валюты она встречается наиболее часто ( 3 раза).
Табл.11.
| № пункта | ||||||||
| Цена за 1 $ |
Медиана 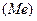 – это величина признака, которая делит численность упорядоченного вариационного ряда на две равные части.
– это величина признака, которая делит численность упорядоченного вариационного ряда на две равные части.
Для примера возьмём данные табл.10 и расположим индивидуальные значения признака в возрастающем порядке.
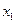
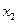

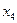
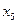
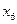
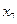
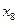
2150 2155 2155 2155 2160 2165  2165 2175
2165 2175
Порядковый номер медианы определяется по формуле
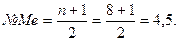
а) В случае чётного числа 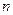 номер медианы имеет не целое значение (в нашем случае 4,5). Медиана будет равна средней арифметической из соседних значении
номер медианы имеет не целое значение (в нашем случае 4,5). Медиана будет равна средней арифметической из соседних значении 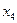 и
и 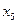
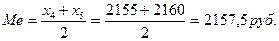
б) В случае нечётного числа индивидуальных признаков (допустим, 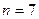 )
)
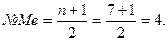
Следовательно, в этом случае 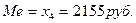
В рассмотренном примере нахождение таких средних, как мода и медиана, было целесообразно, поскольку исследователь не располагал объёмом продаж по каждому пункту и не мог поэтому с хорошей точностью провести расчёт средней арифметической цены за доллар. Также рассмотренный пример иллюстрирует положение о том, что выбор вида соответствующей средней всегда зависит от имеющихся в наличии данных.
4.3. Свойства и методы расчёта средних величин
Наиболее часто используемая в экономико-статистической практике средняя арифметическая величина обладает рядом математических свойств, которые иногда упрощают её расчёт. Эти свойства следующие:
1. Если варианты уменьшить или увеличить на некоторое постоянное число, то
средняя арифметическая величина соответственно уменьшится или увеличится на это
число
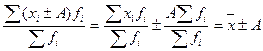
2. Если варианты изменить в постоянное число раз 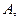 то средняя тоже изменится во
то средняя тоже изменится во
столько же раз

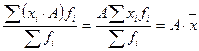
3. Если частоты разделить или умножить на некоторое постоянное число, то средняя не изменится
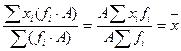
4. Произведение средней арифметической на сумму частот равно сумме произведений вариантов на частоты
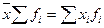
5. Алгебраическая сумма отклонения вариантов от средней величины равна нулю
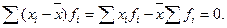
Все перечисленные свойства следуют из определения средней арифметической взвешенной (см.раздел 4.2).
Иногда расчёт средней арифметической величины удобно упростить, используя её математические свойства. Для этого нужно из всех вариант вычесть произвольную постоянную величину, полученную разность разделить на общий множитель, а затем исчисленную среднюю величину умножить на общий множитель и прибавить произвольную постоянную. В результате формула средней арифметической взвешенной получит следующий вид:
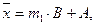 где
где 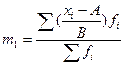 .
.
Средняя величина 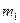 из значений вариант
из значений вариант 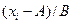 называется моментом первого порядка, а способ вычисления средней – способом моментов.
называется моментом первого порядка, а способ вычисления средней – способом моментов.
При выборе и расчёте вида средней величины необходимо учитывать наличие и характер исходных данных. Следует придерживаться следующего алгоритма.
1) Написать определяющее для расчёта среднего показателя соотношение, которое представляет собой суть связи между показателями задачи и определяет методологию расчёта обобщенного показателя. Например, если требуется определить среднюю месячную заработную плату работников, то таким соотношением является
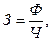
где 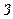 – средняя заработная плата;
– средняя заработная плата; 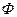 – фонд заработной платы;
– фонд заработной платы; 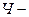 численность работников.
численность работников.
2) Изучить исходные данные и установить наличие показателей в определяющем соотношении. В предложенном примере такими показателями являются 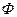 и
и 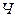 . Если какой-либо показатель отсутствует, то его необходимо определить по исходным данным, пользуясь определяющим соотношением. Например, при наличии данных о фондах заработной платы
. Если какой-либо показатель отсутствует, то его необходимо определить по исходным данным, пользуясь определяющим соотношением. Например, при наличии данных о фондах заработной платы 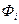 и средней заработной плате
и средней заработной плате 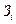 по группам работников, недостающие показатели находятся в виде
по группам работников, недостающие показатели находятся в виде
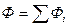
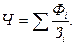
3) Подставить недостающие показатели в определяющее соотношение и установить вид средней. В нашем примере
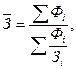
т.е. в этом случае расчёт средней заработной платы можно выполнить по формуле средней гармонической взвешенной (см. раздел 4.2).
Соотношения для определения средних структурных величин, представленные в разделе 4.2, предназначены для расчётов средних величин дискретных рядов. Методы расчёта средних по данным интервальных рядов имеют специфику, связанную с тем, что исследователь имеет дело не с дискретными значениями, а с интервалами группировочного признака. В этих случаях определения степенных средних сохраняются с учётом, что вместо значений вариант в них подставляются серединные значения интервалов.
Для расчёта моды по данным интервального ряда используется следующая формула:
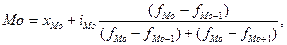
где 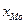 - нижняя граница модального интервала;
- нижняя граница модального интервала;
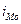 - размер модального интервала;
- размер модального интервала;
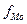 - частота модального интервала;
- частота модального интервала;
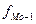 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
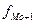 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Для расчёта медианы в интервальном ряду используется следующая формула:

где 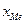 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
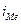 - размер медианного интервала;
- размер медианного интервала;
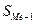 - сумма накопленных частот до медианного интервала;
- сумма накопленных частот до медианного интервала;
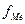 - частота медианного интервала;
- частота медианного интервала;
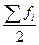 - полусумма частот ряда.
- полусумма частот ряда.
Дата добавления: 2017-11-04; просмотров: 943;
