Анализ эффективности финансовых вложений и инвестиционной политики компаний
Финансовые вложения – расходы (инвестиции) предприятия на приобретение ценных бумаг (акций и облигаций, в том числе государственных), паевые вклады в уставные капиталы других организаций, займы юридическим и физическим лицам. Для анализа эффективности финансовых вложений могут применяться те же методы, что и при анализе капитальных вложений. Кроме того, могут быть рассчитаны показатели инвестиционной привлекательности фирмы, использующие информацию об операциях с ее ценными бумагами. Эти показатели также характеризуют финансовую устойчивость предприятия. Поскольку большинство предприятий в России являются акционерными обществами, то из всех видов ценных бумаг в первую очередь анализируются акции.
Финансовое инвестирование - это активная форма эффективного использования временно свободных средств предприятия. Это вложение капитала в:
• доходные фондовые инструменты (акции, облигации и другие ценные бумаги, свободно обращающиеся на денежном рынке);
• доходные виды денежных инструментов, например депозитные сертификаты;
• уставные фонды совместных предприятий с целью не только получения прибыли, но и расширения сферы финансового влияния на другие субъекты хозяйствования, и др.
В процессе анализа изучаются объем и структура инвестирования в финансовые активы, определяются темпы его роста, а также доходность финансовых вложений в целом и отдельных финансовых инструментов.
Ретроспективная оценка эффективности финансовых вложенийпроизводится путем сопоставления суммы полученного дохода от финансовых инвестиций со среднегодовой суммой данного вида активов. Средний уровень доходности (ДВК) может измениться за счет: структуры ценных бумаг (УДi), имеющих разный уровень доходности; уровня доходности каждого вида ценных бумаг, приобретенных предприятием (ДВКi)
ДВКобщ = ∑ (Удi * ДВКi).
Таблица 4 - Анализ эффективности использования долгосрочных финансовых вложений
| Показатель | Прошлый год | Отчетный год | Изменение |
| Сумма долгосрочных финансовых вложений, тыс. руб. | +1500 | ||
| В том числе: в акции совместного предприятия | +500 | ||
| в облигации | +1000 | ||
| Удельный вес, %: акций | 50,0 | 46,67 | -3,33 |
| облигаций | 50,0 | 53,33 | +3,33 |
| Доход, тыс. руб.: от акций | +250 | ||
| от облигаций | +300 | ||
| Доходность, %: | 32,5 | 34,66 | +2,16 |
| акций | +5 | ||
| облигаций | - |
Данные табл. 4 показывают, что доходность финансовых вложений за отчетный год повысилась на 2,16%, в том числе за счет изменения:
структуры финансовых вложений
ΔДВК=∑ (ΔУДi * ДВКi 0) = [(-3,33) * 35 + (+3,33) * 30] / 100 = -0,17%;
уровня доходности отдельных видов инвестиций
ΔДВК=∑ (УДi * ΔДВКi) = (46,67 * 5 + 53,33 * 0) / 100 = +2,33%.
Доходность ценных бумаг необходимо сравнивать также с так называемым альтернативным (гарантированным) доходом, в качестве которого принимается ставка рефинансирования или процент, получаемый по государственным облигациям или казначейским обязательствам.
Прогнозирование экономической эффективности отдельных финансовых инструментовможет производиться с помощью как абсолютных, так и относительных показателей. В первом случае определяется текущая рыночная цена финансового инструмента, по которой его можно приобрести, и внутренняя его стоимость исходя из субъективной оценки каждого инвестора. Во втором случае рассчитывается относительная его доходность.
Различие между ценой и стоимостью финансового актива состоит в том, что цена — это объективный декларированный показатель, а внутренняя стоимость - расчетный показатель, результат собственного субъективного подхода инвестора.
Текущая внутренняя стоимость любой ценной бумаги в общем виде может быть рассчитана по формуле:
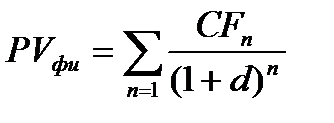 ,
,
где РVфи - реальная текущая стоимость финансового инструмента;
CFn - ожидаемый возвратный денежный поток в n-м периоде;
d - ожидаемая или требуемая норма доходности по финансовому инструменту;
n - число периодов получения доходов.
Подставляя в данную формулу значения предполагаемых денежных поступлений, доходности и продолжительности периода прогнозирования, можно рассчитать текущую стоимость любого финансового инструмента.
Если фактическая сумма инвестированных затрат (рыночная стоимость) по финансовому инструменту будет превышать его текущую стоимость, то инвестору нет смысла приобретать его на рынке, так как он получит прибыль меньше ожидаемой. Напротив, держателю этой ценной бумаги выгодно продать ее в данных условиях.
Как видно из приведенной формулы, текущая стоимость финансового инструмента зависит от трех основных факторов: ожидаемых денежных поступлений, продолжительности прогнозируемого периода получения доходов и требуемой нормы прибыли. Горизонт прогнозирования зависит от вида ценных бумаг. Для облигаций и привилегированных акций он обычно ограничен, а для обыкновенных акций равен бесконечности.
Требуемая норма прибыли, закладываемая инвестором в алгоритм расчета в качестве дисконта, отражает, как правило, доходность альтернативных данному инвестору вариантов вложения капитала. Это может быть размер процентной ставки по банковским депозитам, уровень процента по правительственным облигациям и т.д.
Особенности формирования возвратного денежного потока по отдельным видам ценных бумаг обусловливают разнообразие моделей определения их текущей стоимости.
Базисная модель оценки текущей стоимости облигаций с периодической выплатой процентоввыглядит следующим образом:
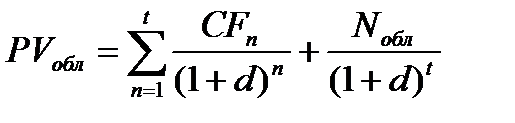 ,
,
где PVoбл - текущая стоимость облигаций с периодической выплатой процентов;
CFn - сумма полученного процента в каждом периоде (произведение номинала облигации на объявленную ставку процента (Noбл * k));
Noбл - номинал облигации, погашаемый в конце срока ее обращения (t);
k - годовая купонная ставка процента.
Пример.
Требуется определить текущую стоимость трехлетней облигации, номинал которой 1000 руб., с купонной ставкой 8% годовых, выплачиваемых раз в год, если норма дисконта (рыночная ставка) равна 12% годовых.
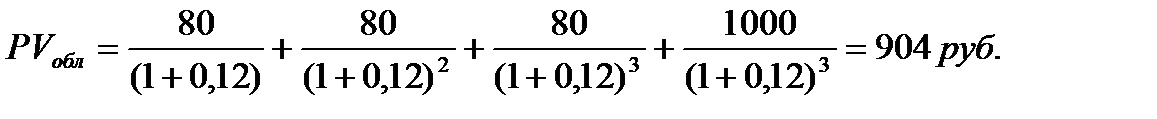
Следовательно, норма доходности в 12% будет обеспечена при покупке облигации по цене, приблизительно равной 900 руб.
Если требуемая норма доходности составляет 6%, то текущая стоимость облигации будет равна:
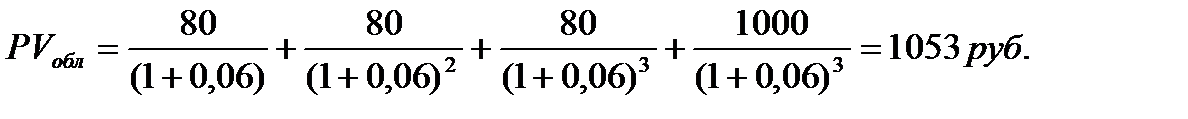
Отсюда видно, что текущая стоимость облигации зависит от величины рыночной процентной ставки и срока до ее погашения. Если d > k, то текущая стоимость облигации будет меньше номинала, т.е. облигация будет продаваться с дисконтом Если d < k, то текущая стоимость облигации будет больше номинала, т.е. облигация продается c премией. Если d = k, то текущая стоимость облигации равна ее номиналу.
Если доходность облигации не меняется в течение срока ее обращения, то по мере уменьшения срока до погашения величина дисконта или премии будет падать. Причем эти изменения более существенны по мере приближения срока погашения.
Доход по купонным облигациям состоит из периодических выплат процентов (купонов) и из курсовой разницы между рыночной и номинальной ценой облигации. Поэтому для характеристики доходности купонных облигаций используется несколько показателей:
а) купонная доходность, ставка которой объявляется при выпуске облигаций;
б) текущая доходность, представляющая собой отношение процентного дохода к цене покупки облигации:
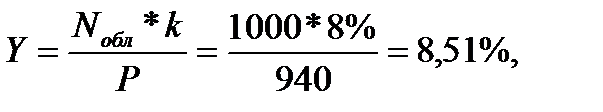
где Nобл – номинал облигации;
k – купонная ставка процента;
Р – цена покупки облигации.
в) доходность к погашению:
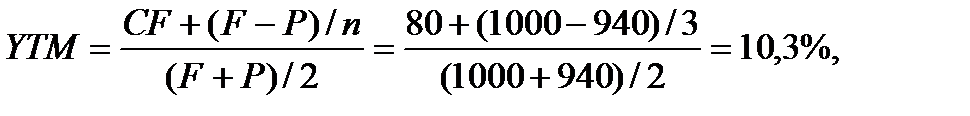
где F - цена погашения;
Р - цена покупки;
GF - сумма годового купонного дохода по облигации;
n - число лет до погашения.
Модель оценки текущей стоимости облигаций с выплатой всей суммы процентов при ее погашении:
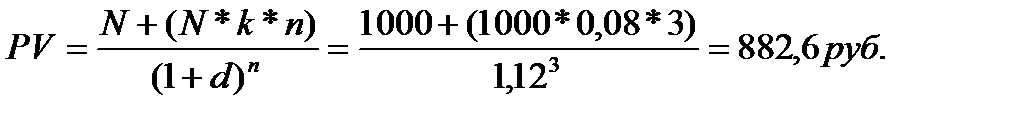
где N*k*n – сумма процентов по облигации, выплачиваемых в конце срока ее обращения.
Модель оценки текущей стоимости облигаций, реализуемых с дисконтом без выплаты процентов:
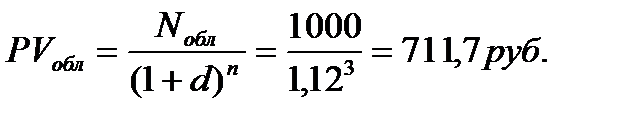
Модель доходности дисконтных облигаций:
а) по эффективной ставке процента
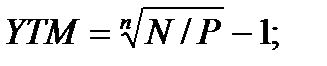
б) по ставке простых процентов
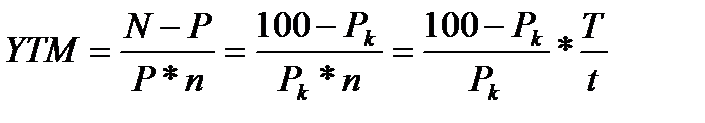 ,
,
где Pk – курс облигации (отношение цены покупки к номинальной стоимости облигации);
Т - количество календарных дней в году;
t - количество дней до погашения облигации.
Предположим, требуется определить уровень доходности облигаций к погашению, если цена покупки — 850 руб., цена выкупа (номинал) — 1000 руб., срок обращения облигации — 90 дней:
а) по эффективной ставке процента
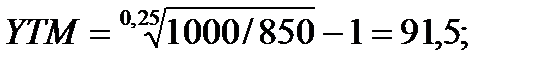
б) по ставке простых процентов
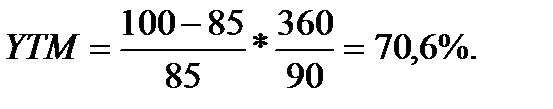
Для оценки текущей стоимости акции при ее использовании в течение неопределенного срока применяют обычно следующую модель:
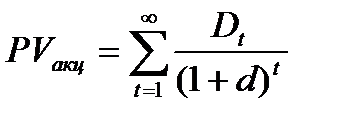 ,
,
где PVакц – текущая стоимость акции, используемой в течение неопределенного периода времени;
Dt – предполагаемая к получению сумма дивидендов в t-м периоде;
d - альтернативная норма доходности в виде десятичной дроби;
t - число периодов, включенных в расчет.
Текущая стоимость акций со стабильным уровнем дивидендов определяется как отношение суммы годового дивиденда к рыночной норме доходности:
PVaкц = Di / d = 200 / 0,15 = 1333 руб.
Для определения текущей стоимости акций, используемых в течение определенного срока, применяют следующую модель:
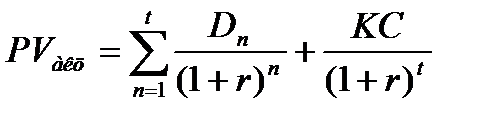 ,
,
где КС - курсовая стоимость акции в конце периода ее реализации;
n - число периодов использования акции.
Пример.
Номинальная стоимость акции - 1000 руб., уровень дивидендов - 20%, ожидаемая курсовая стоимость акции в конце периода ее реализации - 1100 руб., рыночная норма доходности - 15%,период использования акции - 3 года, периодичность выплаты дивидендов - один раз в году.
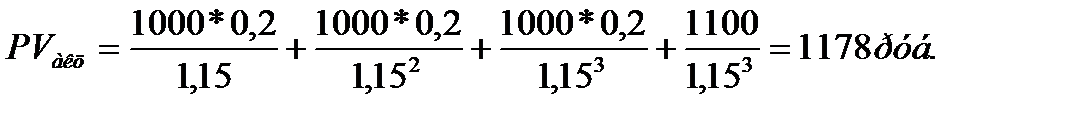
Доход от акций состоит из суммы полученных дивидендов и дохода от прироста их стоимости. Текущая доходность определяется отношением суммы дивидендов по акции за последний год к курсовой стоимости акции:
Yтeк = D / Pa * 100%.
Курсовая стоимость акции рассчитывается в сравнении с банковской депозитной ставкой (rd):
Pa = D / rd * 100%.
Конечная доходность акции (Y) - это отношение суммы совокупного дохода к первоначальной ее стоимости:
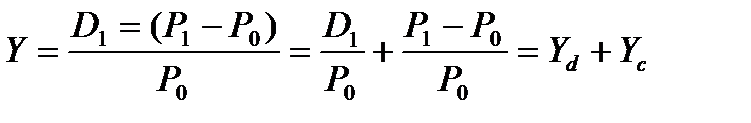 ,
,
где D1 - доход в виде полученных дивидендов;
P1 - рыночная цена акции на текущий момент, по которой она может быть реализована;
Р0 - цена покупки акции;
Yd - дивидендная доходность акции;
Yc - капитализированная доходность акции.
Предположим, предприятие приобрело два года назад пакет акций по цене 10 тыс. руб. за каждую. Текущая рыночная цена акции составляет 15 тыс. руб., а сумма полученных дивидендов на одну акцию за этот период - 3 тыс. руб. Отсюда суммарный доход от одной акции равен 8 тыс. руб. [3 + (15 - 10)], а общая ее доходность составляет 80% (8/10 * 100), в том числе дивидендная доходность - 30% (3/10 * 100), капитализированная доходность - 50% [(15 -10): 10 * 100].
Пользуясь приведенными моделями, можно сравнивать выгодность инвестиций в различные финансовые инструменты и выбирать наиболее оптимальный вариант инвестиционных проектов.
Уровень доходности инвестиций в конкретные ценные бумаги зависит от:
• изменения уровня процентных ставок на денежном рынке ссудных капиталов и курса валют;
• ликвидности ценных бумаг, определяемой временем, которое необходимо для конвертации финансовых инвестиций в наличные деньги;
уровня налогообложения прибыли и прироста капитала для разных видов ценных бумаг;
• размера трансакционных издержек, связанных с процедурой купли-продажи ценных бумаг;
• частоты и времени поступления процентных доходов;
• уровня инфляции, спроса и предложения и других факторов.
Дата добавления: 2017-11-04; просмотров: 382;
