Парная линейная корреляция
Корреляционные связи одних явлений с другими видны уже на первых стадиях статистической обработки данных. Сводка и группировка статистических показателей, исчисление относительных и средних величин, построение вариационных, динамических, параллельных рядов позволяет установить наличие взаимосвязи изучаемых явлений и даже ее характер (прямой и обратный).
Парная линейная корреляция– это связь между факторным признаком и результативным признаком. Определение парной корреляции находит широкое применение в судебной статистике. Корреляционное измерение связи часто производится после установления ее наличия и направленности (прямая, обратная).
Рассмотрим этапы расчета парного коэффициента корреляции, для этого воспользуемся данными двух статистических рядов, характеризующими количество административных правонарушений (х) и преступлений (у) с 1991 по 1997 годы. Если между показателями х и у существует прямая корреляционная связь, от необходимо абстрагироваться от влияния других факторов.
| Годы | |||||||
| Число правонарушений (х) | |||||||
| Число преступлений (у) |
В таблице годы расположены не в хронологическом порядке, а в порядке возрастания количества правонарушений.
На первом этапе для устранения влияния других факторов необходимо выполнить аналитическое выравнивание по прямой фактического ряда преступлений (у). Для выравнивания ряда может быть применено следующее уравнение
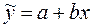 ,
,
где 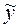 - значение выровненного ряда результативного признака (преступлений),
- значение выровненного ряда результативного признака (преступлений), 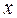 - реальное значение факторного признака (правонарушений),
- реальное значение факторного признака (правонарушений), 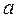 и
и 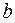 - параметры, вычисляемые методом наименьших квадратов.
- параметры, вычисляемые методом наименьших квадратов.
На втором этапе определяются параметры 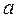 и
и 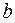 способом наименьших квадратов. Для этого решается система уравнений
способом наименьших квадратов. Для этого решается система уравнений
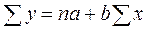 ,
,
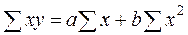 .
.
Для приобретения навыков расчета коэффициента корреляции будем считать, что в результате выполнения первого и второго этапа расчета значения выровненного ряда 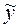 совпали с реальными значениями результативного признака
совпали с реальными значениями результативного признака  .
.
На третьем этапе производится расчет коэффициента корреляции по формуле:
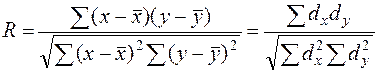 ,
,
где 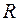 - коэффициент корреляции,
- коэффициент корреляции,  - отклонение от среднего значения признака-фактора,
- отклонение от среднего значения признака-фактора,  - отклонение от среднего значения признака-результата. Для выполнения расчета необходимо найти средние значения
- отклонение от среднего значения признака-результата. Для выполнения расчета необходимо найти средние значения 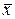 и
и 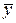 факторного и результативного признаков, а также отклонения значений признаков от средних величин
факторного и результативного признаков, а также отклонения значений признаков от средних величин 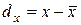 и
и 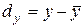 . Расчет требуемых величин покажем при помощи таблицы.
. Расчет требуемых величин покажем при помощи таблицы.
| № п/п | 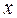
| 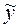
| 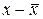
| 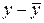
| 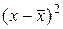
| 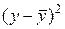
| 
|
| -27,29 | -1,43 | 744,51 | 2,04 | 38,98 | |||
| -20,29 | -2,43 | 411,51 | 5,90 | 49,27 | |||
| -6,29 | -3,43 | 39,51 | 11,76 | 21,55 | |||
| 2,71 | 0,57 | 7,37 | 0,33 | 1,55 | |||
| 9,71 | -0,43 | 94,37 | 0,18 | -4,16 | |||
| 13,71 | 2,57 | 188,08 | 6,61 | 35,27 | |||
| 27,71 | 4,57 | 768,08 | 20,90 | 126,69 | |||
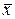 =65,29 =65,29
| 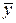 =7,43 =7,43
| 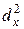 =2253,43 =2253,43
| 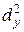 =47,71 =47,71
| 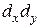 =269,14 =269,14
|
Подставляя полученные значения, в формулу для расчета коэффициента корреляции получим:
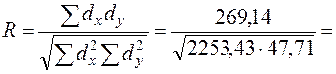 0,82.
0,82.
Коэффициент корреляции между совершенными административными правонарушениями и преступлениями принял значение 0,82, что свидетельствует о наличии прямой связи между изучаемыми явлениями и эта связь достаточно близка к функциональной.
Дата добавления: 2017-10-09; просмотров: 729;
