Процентные ставки и доходность основных ценных бумаг.

Более всего финансовая наука связана с анализом прибыльности инвестиционной деятельности. Цель инвестиций - увеличение благосостояния инвестора. Это увеличение называется доходом, а при выражении в процентах от стоимости инвестиций - став­кой дохода. Кроме измерения доходности финансовые аналити­ки имеют дело также с неопределенностью получения дохода, с этой неопределенностью связан анализ риска. В этой лекции мы сосредоточимся на измерении доходности, а в следующих рассмотрим различные виды и аспекты рисков.

Инвесторы приобретают активы такие, как акции компаний, облигации или недвижимость, в надежде получить доход либо от продажи их по более высокой цене, либо в виде дивидендов, про­центов по купонам или в виде рентных платежей. Кредиторы ссужают деньги в надежде получить доход в виде процентных платежей при полном погашении кредита заемщиком. Таким образом, кредиторы и инвесторы имеют общую цель - получить доход, или процент, как результат инвестиционной или кредиторской деятельности.

Процентные ставки, вероятно, - наиболее часто используемые фи­нансовые показатели. Многие экономические агенты берут кредит и платят проценты по этому кредиту. Многие помещают деньги в банк или другое финансовое учреждение и получат за это процентные платежи. Известно, что су­ществует большое разнообразие процентных ставок по кредитам и вкладам. Эти ставки отличаются не только по величине, но и по методу их вычисления. Одни процентные ставки фиксированы в течение всего периода действия договора, другие же могут изме­няться на оговоренных условиях в определенные промежутки вре­мени. Существуют и такие, например, по ипотечным ссудам, кото­рые могут меняться по желанию кредитора. Но почему же вообще выплачиваются проценты по кредитам и депозитам?

Чтобы ответить на этот вопрос, необходимо осознать, что деньги приносят выгоду или обеспечивают благосостояние толь­ко косвенно, являясь средством обмена. Это означает, что они должны быть обменены на другие товары или услуги, чтобы принести прямую пользу. Следовательно, деньги сами по себе (банкноты, монеты, банковские счета) мало удовлетворяют жизненные потребности. Это происходит путем обмена денег на то­вары и услуги, такие, как продукты питания, одежда и жилье.

Таким образом, когда кто-либо инвестирует деньги, он отка­зывается от возможности обратить их в товары и услуги, которые приносят пользу напрямую. Поэтому ему придется довольство­ваться более низким уровнем полезности, чем если бы деньги были употреблены для приобретения товаров и услуг вместо ин­вестирования. Эта потеря потенциальной полезности должна быть компенсирована - в этом состоит важнейшая функция процента.

Далее, кредитор сталкивается со значительной неопределен­ностью относительно стоимости денег, когда они к нему воз­вращаются (будущая стоимость этих денег неопределенна). Ко­личественная мера этой неопределенности известна как риск. Кредиторы встречаются с различными видами рисков, и это мо­жет уменьшить их выгоду или благосостояние. Одной из функ­ций процента является компенсация этой потери выгоды, суще­ствующей из-за рисков.

Первый вид риска, который мы рассмотрим - это риск поте­ри покупательной способности, более известный как инфляцион­ный. Если экономика характеризуется наличием инфляции в пе­риод инвестирования суммы денег или выдачи займа, на эту сумму можно будет приобрести меньшее количество товаров и услуг, когда они будут возвращены, чем до выдачи займа или инвестирования. Поэтому инвесторы будут требовать компенса­ции за потерю покупательной способности.

Второй вид риска - это то, что деньги могут быть не воз­вращены вследствие либо неудачи проекта, либо обмана со сто­роны заемщика, или других непредвиденных обстоятельств. Этот риск называется риском невыполнения обязательств, и снова ин­весторы должны получить компенсацию за него.

Если мы объединим риск потери потенциальной выгоды, инфляционный риск и риск невыполнения обязательств, мы по­лучим группу факторов, которые делают обладание деньгами в настоящем более предпочтительным по сравнению с их облада­нием в будущем. Люди предпочитают иметь деньги сейчас, чем довольствоваться обещаниями получить их позднее. О деньгах говорят, что они характеризуются положительным временным предпочтением(positive time preference).

Проценты компенсируют заимодавцу невозможность удовле­творить эти предпочтения в момент инвестирования средств. Заемщики готовы заплатить за использование средств, потому что это позволяет им иметь дополнительную выгоду раннего по­требления в результате получения средств от инвестора.

Из того, что было изложено, должно быть ясно, что сущест­вует множество процентных ставок. В любое время на финансо­вых рынках существует ряд процентных ставок, поэтому полезно разделить факторы, определяющие эти ставки, на две группы: те, которые определяют общий уровень процентных ставок, и те, которые определяют различие процентных ставок.

Факторы, влияющие на уровень процентных ставок:

• политика правительства

• денежная масса

• ожидания относительно будущей инфляции.

Факторы, влияющие на различие процентных ставок:

• время до погашения финансовых обязательств

• риск невыполнения обязательств

• ликвидность финансовых обязательств

• налогообложение

• другие различные факторы, специфические для конкретных
финансовых обязательств, например, предоставлено ли обес­печение активами, включены ли права выбора в договор.

4.1. Временная стоимость денег.

Временная стоимость денег имеет отношение к процессу опре­деления текущей стоимости, т.е. сегодняшней стоимости суммы, обещанной в какой-либо момент в будущем, или к расчету буду­щей стоимости, т.е. стоимости суммы в будущем, полученной или уплаченной сегодня. Процесс определения текущей стоимости денег называется дисконтированием, а будущей - наращением.

Текущая стоимость находится путем дисконтирования каждого из потоков платежей на процент, который мог бы быть зарабо­тан, если бы эти средства были получены сегодня. Наиболее распространенное применение дисконтирования - это оценка облигаций путем дисконтирования будущих купонных платежей, а также оценка акций на основе использования модели дискон­тирования дивидендов. Оба эти приложения продемонстрирова­ны ниже в этой главе.

Финансовые активы оцениваются при помощи расчета теку­щей стоимости ожидаемых потоков платежей от этих активов. Некоторые финансовые инструменты, такие, как фьючерсы и форварды, оцениваются исходя из будущей стоимости денег. Бу­дущая стоимость находится наращением всех процентных плате­жей, которые можно было бы получить на данную сумму до на­ступления определенного момента в будущем.

4.1.1. Простые проценты.

Предположим, что первоначальная сумма РV была помещена в банк под r процентов годовых. Тогда через время n (периодов) наращенная сумма FV составит величину:

FV = PV * (1+ r * n) (4.1).

Соглашения по подсчету дней.

Одна из сложностей, которая возникает при вычислении простых процентов, - это соглашения, принятые на данном конкретном рынке по подсчету количества дней. По всем финансовым инст­рументам наращение происходит ежедневно, однако существуют расхождения между разными рынками в подсчете процентов - одни берут за основу 360 дней в году, а другие - 365 дней или 366 в високосном году. Кроме того, на некоторых рынках принимает­ся в месяце 30 дней, независимо от их реального количества. В Великобритании по денежным инструментам, деноминированным в фунтах стерлингов, используют 365 дней в году при начислении процентов. Во многих других финансовых центрах, а также в Лон­доне по финансовым инструментам, деноминированным не в фунтах стерлингов, расчет ведется из 360 дней в году.

Таким образом, в случае 360 дней в году процентные плате­жи, уплачиваемые по, скажем, 45-дневному депозиту, рассчи­тываются исходя из общего срока, равного 45/360 лет. Этот ме­тод обозначается как АСТ/360 (actual over 360). Если же про­центные платежи рассчитываются исходя из 365 дней в году, тогда для 45-дневного депозита срок в годах выражается через 45/365. Этот метод носит название АСТ/365 (actual over 365).

4.1.2. Сложные проценты.

Предположим, что первоначальная сумма РV была помещена в банк под r процентов годовых. В конце года банк начисляет по вкладу проценты и причисляет их к основной сумме вклада. Тогда через n лет наращенная сумма FV составит величину:

FV = PV * (1+ r) 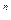(4.2).

Эта формула используется при вычислении будущей стоимости капитала. PV – это настоящая стоимость.

В формуле 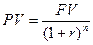величина 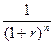называется коэффициентом дисконтирования, величина r называется ставкой процента, выраженной в долях единицы, под которую размещается текущая стоимость; величина n называется числом периодов начисления процентов по ставке r.

Пример: В конце третьего года на счете инвестора находится сумма 15 972 руб. Начисление происходило по схеме сложного процента по ставке 10% годовых в конце каждого года. Рассчитайте первоначальную сумму вклада.

Ответ: 12 000 руб.

Пример: Банк выплачивает сложные проценты. Какую минимальную процентную ставку должен обеспечить банк для того, чтобы вкладчик удвоил свои средства за 5 лет?

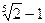Решение: 2 = 1* (1+ r) или r = = 1.15 – 1 = 0.15 или 15%.

Пример: Банк выплачивает сложные проценты. Вкладчик разместил в банке 18 000 руб. Сколько лет потребуется вкладчику для того, чтобы его вклад достиг 31 100 руб., если банк выплачивает 20% годовых.

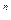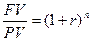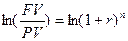Решение: FV = PV*(1+r) или или или

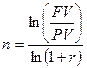. Тогда n = 3.

Простейший вид финансовой сделки – однократное предоставление в долг некоторой суммы PV с условием, что через время Т будет возвращена сумма FV. Для определения эффективности сделки используют две величины:

относительный рост (интерес, interest rate, return)

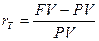(4.3)

и относительную скидку (дисконт, discount rate)

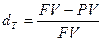(4.4).

Обе величины характеризуют приращение капитала кредитора или дилера, отнесенное либо к начальному вкладу (интерес), либо к конечной сумме (дисконт).

Очевидно, что все введённые величины взаимосвязаны:

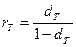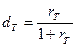, (4.5),

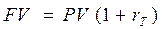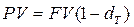, (4.6).

Последние формулы показывают, что сделку удобно характеризовать либо как «начальная сумма - интерес», либо как «конечная сумма – дисконт». Иногда вместо дисконта используют дисконт-фактор:

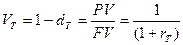(4.7).

Как правило, и рост, и дисконт выражаются в процентах, умножая соответствующие величины на 100. Эта традиция настолько сильна, что вместо термина «рост» часто говорят «ставка процента».

4.1.3. Эффективная ставка.

Эффективной называется годичная ставка сложных процентов, дающая то же соотношение между выданной суммой S(0) и суммой S(T), которая получена при любой схеме выплат. Мера доходности к погашению недооценивает возможные поступления от реинвестирования выплат по облигациям. Строго говоря, любая ставка, рассчитанная с учетом эффекта сложных процентов, называется эффективной.

Общая формула эффективной ставки 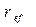следует из определения

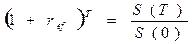(4.8)

откуда 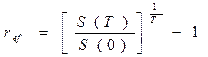(4.9),

где Т выражено в годах. Расчет эффективной ставки 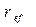- один из основных инструментов финансового анализа. Знание его позволяет сравнивать между собой сделки, построенные по различным схемам: чем выше эффективная ставка, тем (при прочих равных условиях) выгоднее сделка для кредитора.

Мера доходности к погашению недооценивает возможные поступления от инвестирования выплат по облигациям. Показатель, учитывающий эффект сложных процентов, называется эффективной доходностью. Между доходностью к погашению и эффективной доходностью существует следующая взаимосвязь. Если «у» - доходность за один купонный период, то годовая эффективная доходность 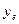рассчитывается как

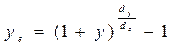(4.10),

где 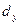- количество дней в году, 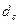- количество дней в купонном периоде. Пример: Годовая доходность к погашению облигации составляет 40% годовых, или 10% в квартал, купонный период – 91 день, а количество дней в году – 365. Определить эффективную доходность к погашению такой облигации.

Решение. Она равна: .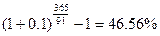

4.1.4. Оценка потока платежей.

Многие финансовые контракты, в том числе контракты, оформленные в виде рыночных ценных бумаг, предусматривают не однократную выплату в конечный момент, а многократные выплаты в различные промежутки времени. Взаимоотношения между кредитором и дебитором в общем случае определяются потоком платежей.

Предположим, что некто купил облигацию, которая гарантировано должна приносить купонные доходы в размере 1 тыс. руб. в течение 10 лет в конце каждого года. Предположим также, что это физическое лицо открыло в банке счет до востребования, на который будут зачисляться купонные выплаты. Вычислить сумму, которой будет обладать на счете этот человек через 10 лет после его открытия, если банк по таким счетам начисляет r % годовых.

В конце 1-го года на счете окажется 1 тыс. руб.

В конце 2-го года на неё будут начислены проценты и добавится ещё 1 тыс. руб. или 1 тыс. руб.*(1 + (1 + r)).

В конце 3-го года 1 тыс.руб. *(1 + (1 + r)*[1+(1+r)]) и так далее.

Конечный результат можно представить в виде:

S(10)=1000*(1+(1+r)[1+(1+r[1+…+1+r])…])=1000*(1+(1+r)+(1+r) 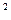+(1+r) 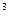+…+(1+r) 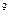) = 1000 * .

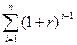Это есть геометрическая прогрессия вида 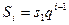. Сумма всех членов геометрической прогрессии равна:

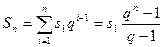(4.11).

В нашем случае q=(1+r), тогда

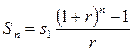(4.12).

Так, при r = 5% годовых, S(10) = 12 578 руб.

Необходимо подчеркнуть, что это есть прямой счет от S(0) к S(10). Во многих ситуациях представляет интерес приведение всех платежей к исходному данному моменту с учетом дисконтирования платежей, приходящих в будущем. Результат приведения называется современной или приведённой величиной (present value, PV). В общем случае это будет равенство следующего вида:

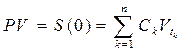(4.13).

Для постоянной ренты с поступлением в конце каждого года и ежегодным начислением по ставке r имеем за n лет:

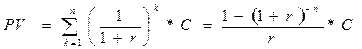(4.14).

Смысл PV очень прост: это начальная сумма, вложив которую под те же проценты, можно обеспечить возможность выплаты из неё всех рентных платежей.

4.1.5. Двусторонний поток платежей, чистая приведённая величина.

Финансовая операция может предусматривать неоднократные и разновременные переходы денежных сумм от одного владельца к другому. Рассматривая поток платежей с позиции одного из них, можно считать все поступления к нему положительными величинами, а все выплаты – отрицательными. Для оценки финансовой операции в целом используется чистая приведённая величина (net present value, NPV), вычисляемая по формуле 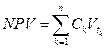, но с учётом знака величины .

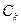Пример: Контракт между фирмой и банком предусматривает, что банк предоставляет в течение 2-х лет кредит фирме ежегодными платежами в размере 1 млн. руб. в начале каждого года под ставку 10% годовых. Фирма возвращает долг, выплачивая 1 и 1.5 млн. руб. в конце 2-го и 3-го годов. Какова NPV этой операции для банка?

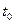
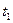
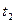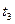+1 +1.5

-1 -1

NPV = -1 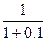– 1* + 1* 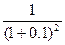+ 1.5 * 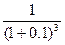= 0.044 млн. руб.

Поскольку результат положителен, то эта операция является для банка приемлемой.

4.1.6. Непрерывная ставка (сила роста) и дисконт.

В теоретическом анализе, а иногда на практике, когда платежи поступают или изымаются многократно за период оценки работы финансового учреждения, удобно предполагать, что накапливаемые суммы непрерывно меняются во времени. Если S(t) – сумма в любой момент времени t, то её скорость роста, производная по времени, по определению равна:

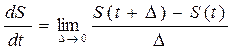(4.15).

Отношение скорости роста к текущему значению называется силой роста или непрерывной ставкой процента ( 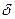дельта):

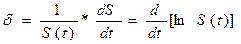, (4.16),

т.е. сила роста является производной натурального логарифма изменяющейся суммы S(t). Величина дельта 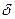также может зависеть от времени. Если сила роста 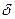(t) задана, то можно найти накопленную за любое время Т сумму:

.

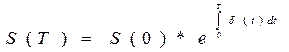При постоянной силе роста 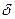(t) = 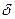= const получаем:

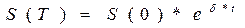(4.17),

где число «е» – основание натурального логарифма, оно равно 2.718.

Приведение дохода с дискретным наращиванием к эквивалентному

доходу с непрерывным наращиванием.

Для преобразования доходов с дискретным наращиванием к доходам с непрерывным наращиванием необходимо, чтобы сумма денег, инвестированная под непре­рывную процентную ставку, имела такую же будущую стои­мость, что и подобная сумма, инвестированная под эквивалент­ную дискретную процентную ставку. Таким образом:

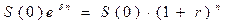или .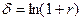

Пример: Инвестор вкладывает в банк сумму равную 1000 рублей под 10% годовых. Процент начисляется непрерывно. Какую сумму денег он получит на счете через 3 года?

Решение: Применяя формулу (4.17) получим: .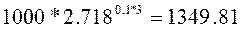

4.2. Оценка стоимости и доходности ценных бумаг.

4.2.1. Облигации.

Выше в этой лекции отмечено, что финансовые инструменты оце­ниваются исходя из суммы текущих стоимостей всех ожидаемых будущих денежных потоков, а фьючерсные и форвардные контракты - по будущей стоимости текущего денежного потока. Здесь мы продемонстрируем использование процентных ставок в процессах дисконтирования и наращивания в оценке банковских депозитных сертификатов, казначейских векселей, облигаций с нулевым купоном, купонных облигаций и акций компаний. По­мимо этого мы рассмотрим, как оцениваются фьючерсные и форвардные контракты. В первую очередь мы должны познако­миться с некоторыми рыночными соглашениями относительно методов наращивания по основным долговым обязательствам, су­ществующим на финансовых рынках.

Уже отмечено выше, что сегодня стоимость некоторой суммы денег, обещанной в будущем, меньше, чем ее будущая стои­мость. Даже в мире, характеризующемся отсутствием рисков, это условие по-прежнему будет выполняться, потому что денежные средства могли быть инвестированы по процентной ставке, сво­бодной от риска. Поэтому будущая стоимость денег, инвестиро­ванных сегодня, будет больше стоимости этой же суммы, обещанной в будущем. В мире, в котором мы живем и который ха­рактерен наличием рисков, существует ряд неопределенностей, касающихся стоимости денег, обещанных в будущем, таких, как инфляция и невыполнение договорных обязательств.

Для сравнения стоимостей различных денежных потоков в разные периоды времени в будущем необходимо дисконтировать будущие потоки наличности и привести их к текущей стоимо­сти. Текущая стоимость - это сумма, которая при инвестирова­нии под существующую процентную ставку до определенной даты платежа имела бы стоимость, равную по величине сумме платежа, обещанного в этот момент в будущем.

Дискретное дисконтирование. Во многих финансовых опера­циях, даже краткосрочных, при дисконтировании используются сложные проценты. В этом случае для дисконтирования будущих денежных потоков и приведения их к текущей стоимости необ­ходимо денежный поток разделить на дисконтный множитель (1 + ставка дисконтирования, выраженная в виде десятичной дроби) в степени, равной количеству лет до получения денежных средств. Это может быть представлено в следующем виде: инвестиционная, или внутренняя стоимость облигации (или акции), в соответствии с методом капитализации дохода есть суммарная сегодняшняя стоимость потока доходов, обеспечиваемых этой облигацией. Будем считать, что фактические будущие выплаты по облигации в точности соответствуют обещанным и равны С1, С2, …. Сn. Доход выплачивается через равные промежутки времени 1, 2, …, n. Инвестиционная стоимость облигации за n купонных периодов до погашения в этом случае равна:

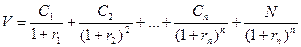(4.18).

Если купонные выплаты и процентная ставка, по которой дисконтируются эти выплаты, будут равны между собой, то инвестиционная стоимость облигации будет:

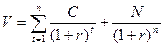(4.19),

или, применяя формулу для суммы геометрической прогрессии,

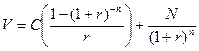(4.20).

Обозначим первое слагаемое в равенстве (4.20) через PV, тогда

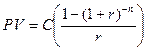(4.21)

представляет собой текущую стоимость аннуитета, а

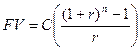(4.22)

- будущую стоимость аннуитета. Для бессрочной облигации уравнение (4.22) значительно упрощается:

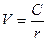(4.23).

Такое же уравнение справедливо и для оценки стоимости акции, по которой выплачиваются стабильные дивиденды в размере d рублей:

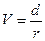(4.24).

Если выплачиваемые дивиденды по акциям из года в год увеличиваются на g процентов, то стоимость акции можно оценить по формуле Гордона:

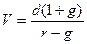(4.25),

где r – ставка дисконтирования.

Непрерывное дисконтирование. Так же, как и в случае с нара­щением, период между процессами дисконтирования может быть уменьшен до такой степени, что дисконтирование проис­ходит непрерывно.

Формула для непрерывного дисконтирования выглядит так:

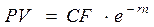(4.26),

где CF – величина денежного потока. Следовательно, при непрерывном дисконтировании число «е» возводится в отрица­тельную степень (-r • n). Например, текущая стоимость 1000 еди­ниц, получаемая через 5 лет и при непрерывном дисконтирова­нии в 10% годовых, равна:

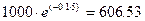ед.

Пример: Рассчитайте рыночную стоимость облигации (Р) номиналом 10 000 руб. с выплатой ежегодного купонного дохода 9% от номинала и сроком погашения через 3 года, если ставка процента по вкладу в банке составляет 11% годовых.

Решение: .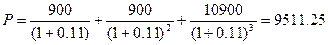

Пример: По акции был выплачен дивиденд в размере 40 руб. на акцию. Инвестор полагает, что в течение последующих лет темп прироста дивиденда составит 8% в год. Доходность равная риску покупки акции равна 19%. Определить цену акции.

Решение. Используяформулу (1.6.6), получим: 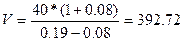руб.

Пример: Инвестор в течение следующих 10 лет в конце каждого года должен выплачивать по своим обязательствам по 30 тыс. руб. Чтобы располагать данными деньгами к концу каждого следующего года, он решает открыть в банке 10-и летний депозит на некоторую сумму денег. По депозиту ежегодно начисляются 6%, средства со счета можно снимать в конце каждого года полностью или частично. Какую минимальную сумму денег необходимо разместить на депозите сегодня, чтобы за счет средств депозита полностью покрыть все свои обязательства?

Решение. По формуле (4.21) PV = 30 000 * (1 – (1 + 0.06)^(-10)) / (0.06) = 220 802.6 руб.

Расчет доходности облигаций:

А) Чистая приведённая стоимость.

Разница между стоимостью облигации и её рыночной ценой есть чистая стоимость (NPV) облигации

NPV = V – P (4.27).

Как для любой инвестиции, положительная величина NPV говорит о выгодности приобретения (недооценённости) облигации, и наоборот, если NPV меньше нуля – облигация переоценена, и её выгодно продать.

Б) Доходность к погашению.

Доходность к погашению (более точно – обещанная доходность к погашению) облигации есть такое значение ставки дисконтирования, при котором суммарная приведённая стоимость платежей по облигации равняется текущей рыночной цене. Доходность к погашению – не что иное, как внутренняя норма доходности инвестиций в данную облигацию. Математически – доходность к погашению есть такое значение «у», для которого выполняется равенство:

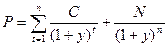(4.28),

где Р – рыночная цена облигации, С – купон, N – номинал, n – количество купонных периодов до момента погашения. Если купонные выплаты производятся чаще, чем один раз в год, полученную величину «у» необходимо привести к годовому измерению, умножив на количество купонных выплат в году. Очевидно, что такой метод расчёта годовой ставки доходности недооценивает эффективную ставку доходности (доходы от реинвестирования). Тем не менее, в большинстве случаев рыночные соглашения предусматривают именно такую процедуру. Показатель, рассчитанный по этой методике, называют ещё эквивалентной доходностью.

Смысл показателя доходности к погашению можно проиллюстрировать с помощью простой аналогии. Доходность к погашению есть эквивалент такой ставки по банковскому депозиту, при которой, разместив сегодня Р рублей, инвестор будет иметь возможность с периодичностью, равной периодичности купонных выплат, снимать со счёта С рублей, а остаток на счёте к моменту погашения облигации составит N рублей.

Курс облигации: 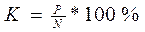, где Р – рыночная цена облигации, а N – номинальная стоимость. Рыночная цена определяется при помощи формулы (4.28).

Пример: Облигация сроком 1 год погашается по номиналу. Выплачивается ежегодный купонный доход в размере 8% от номинала. Рыночная цена облигации составляет 90% от номинала. Чему равна внутренняя ставка доходности?

Решение: 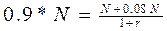, где N – номинал облигации. Откуда r = 20%.

В) Текущая доходность.

Упрощенной мерой доходности облигации является показатель текущей доходности равный отношению купонных выплат в годовом измерении к текущей цене облигации

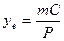(4.29),

где 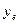- текущая доходность, С – объём одной купонной выплаты, m – количество купонных выплат в году, Р – цена облигации.

Г) Эффективная доходность.

Годовая эффективная доходность 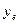рассчитывается как

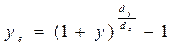(4.30),

где 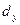- количество дней в году, 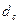- количество дней в купонном периоде. Можно использовать и другой, приближённый, вариант формулы (4.30):

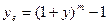(4.31),

где m – количество купонных выплат в году.

Д) Доходность дисконтных облигаций.

По отношению к дисконтным облигациям сроком обращения менее одного года, как правило, рассчитывается простая ставка доходности:

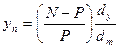(4.32),

где 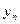- простая ставка доходности в годовом измерении, N – номинальная стоимость облигации, P – текущая цена, 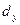- количество дней в году, 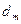- количество дней до погашения.

Пример: Бескупонная облигация А со сроком погашения 5 лет и бескупонная облигация Б со сроком обращения 8 лет имеют равную номинальную стоимость. Когда до погашения облигации А осталось 3 года, а до погашения облигации В осталось 4 года, рыночная стоимость облигации Б составила 85% от рыночной стоимости облигации А. Рассчитайте величину альтернативной годовой доходности.

Решение: 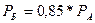или 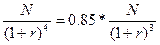или r = 18%.

Е) Накопленный процент.

Если промежуток времени до следующей купонной выплаты меньше одного купонного периода, то при расчёте стоимости облигации необходимо учитывать так называемый накопленный процент – долю от общего объёма купона, которая приходится на время от последней выплаты до сегодняшнего дня. Если промежуток времени до следующей купонной выплаты составляет d дней, а продолжительность одного купонного периода равна 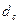дням, то стоимость облигации рассчитывается как

i-ый интервал

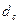
d

t=0 t=1 t=2 t=3 t=4

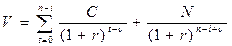(4.33),

где .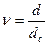

Пример. Номинал бескупонной облигации равен 1000 рублей. Бумага погашается через 2 года и 75 дней. Облигация стоит 845 рублей. Определить доходность облигации к погашению. База 365 дней.

Решение. 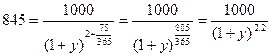. Отсюда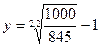

4.2.2. Банковские депозитные сертификаты.

Депозитные сертификаты выдаются банком в обмен на средства, размещаемые у них. Подобные депо­зиты отличаются от обычных банковских депозитов лишь только тем, что сертификаты, подтверждающие наличие срочного депо­зита в банке, могут обращаться на вторичном рынке. Депозитные сертификаты (ДС) выдаются согласно номинальной стоимости, а проценты выплачиваются при погашении, когда возвращается основная сумма.

Рассмотрим два ДС, оба деноминированы в фунтах стерлин­гов, но один выпущен на европейском рынке, а другой - на внутреннем (английском). Каждый из сертификатов имеет срок действия один год и обращается уже в течение 91 дня, ставка доходности по сертификатам составляет 6%. Стоимость ДС размером в 1 000 000 фунтов при погашении составит: первоначальная сумма + накопленные за 365 дней проценты. Однако по ДС на внутреннем рынке про­центы будут начисляться исходя из метода АСТ/365, когда как по евродепозитному сертификату будет применяться метод АСТ/360. Тогда будущие стоимости каждого из них равны:

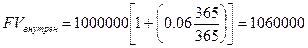
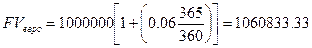
Заметим, что эффективная доходность на еврорынке будет 6*(365/360)= 6,0833.

Депозитный сертификат, обращаясь на вторичном рынке, оценивается исходя из текущей стоимости ожидаемых будущих денежных потоков. Ожидаемые будущие денежные потоки рассчитывают (при отсутствии риска невыполнения обяза­тельств) как было показано выше.

4.2.3. Казначейские векселя.

Казначейский вексель - общий термин для обозначения государственных краткосрочных ценных бумаг со сроком обращения обычно 90 дней, но казначейские векселя могут также иметь сроки как от одного месяца, так и до одного года. Обычно рынок казначейских векселей высоколиквиден, а их эмиссия происходит довольно часто, как правило, еже­недельно (в США).

Казначейские векселя выпускаются по дисконтированной стоимости, а погашаются по номиналу, таким образом, дисконт представляет собой доход инвестора. На наличном рынке каз­начейских векселей их котировка происходит в форме ставок дисконтирования, а не в форме цены. Типичным котиро­вочным предложением может быть 7.0-6.9, что означает жела­ние трейдера покупать вексель по дисконтной ставке 7% годовых, а продавать - по 6.9% годовых.

Доходность казначейского векселя (y) находится при известном дисконте следующим образом:

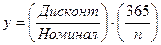(3.34)

при допущении АСТ/365 метода. При вычислении доходности казначейского векселя важно обратить внимание на общий срок его обращения и соответствующий метод подсчета дней, о чем говорилось выше.

4.2.2. Обыкновенные акции.

Один из методов оценки обыкновенных акций состоит в расчете текущей стоимости всех ожидаемых будущих дивидендов, т.е. расчете по так называемой модели дисконтирования дивидендов. Хотя стоимость акций обычно рассматривается как функ­ция ожидаемых будущих доходов, модель дисконтирования ди­видендов расценивает дивиденды как показатель доходов, и та­ким образом учитывает будущие доходы. Это допущение приемлемо при условии, что фирма может либо выплатить при­быль в качестве дивидендов, либо реинвестировать ее в произ­водство. В случае реинвестирования и одновременного приня­тия политики по увеличению дивидендов будущие дивиденды по величине будут больше текущих. Дивиденды будут расти до тех пор, пока часть прибыли направляется на развитие бизнеса. Теоретическая цена обыкновенной акции может быть выраже­на в следующем виде:

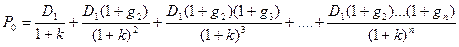(4.34),

где 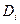- дивиденды, выплачиваемые в конце периода i; 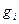- темп роста дивидендов.

Таким образом, текущая цена - это текущая стоимость всех будущих дивидендов. Будущая величина дивидендов находится наращением суммы дивидендов, выплачиваемых в конце теку­щего периода, в соответствии с последующими ожидаемыми темпами роста дивидендов. Например, дивиденды, выплачи­ваемые в конце третьего периода, находятся как ожидаемые ди­виденды в конце первого периода, наращенные за один период исходя из темпов роста 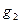затем наращенные для третьего пе­риода исходя из темпов роста .

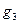Рост прибыли и соответственно дивидендов зависит от того, имеются ли в распоряжении у фирмы финансовые средства для осуществления инвестиций, а также от того, существует ли во­обще возможность для инвестиций. При внешнем финансирова­нии рост будет усилен посредством доходов, получаемых за счет внешнего финансирования проектов. Так как акции являются бессрочными, расчет по вышеприведенной модели трудно выполним, потому что требуется осущест­вить прогноз значений переменных вплоть до бесконечности.

4.3. Математические приложения.

4.3.1. Элементы теории вероятностей и математической статистики.

Случайным событием называется всякий факт, который в результате опыта может произойти или не произойти. Под случайным событием в теории вероятностей понимается неоднократное появление такого события, которое нельзя с полной определенностью предугадать каждый раз.

Классическая схема теории вероятностей охватывает те опыты, элементарные исходы которых удовлетворяют следующим условиям:

1. элементарных исходов – конечное множество;

2. элементарные исходы образуют полную группу попарно несовместных случайных событий, т.е. это означает, что каждый опыт дает в результате один и только один из N элементарных исходов;

3. элементарные исходы равновозможны.

Вероятностью события называется численная мера степени объективной возможности этого события. Вероятность события А обозначается Р(А).

Достоверным называется событие U, которое в результате опыта непременно должно произойти:

Р(U) = 1 (4.35).

Невозможным называется событие V, которое в результате опыта не может произойти:

Р(V) = 0 (4.36).

Вероятность любого события А заключена между нулем и единицей:

.

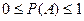Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. Несколько событий в данном опыте называются несовместными, если никакие два из них не могут появиться вместе.

Несколько событий в данном опыте называются равновозможными, если нет оснований считать какое-либо из них более возможным, чем любое другое.

Если несколько событий:

- образуют полную группу;

- несовместны;

- равновозможны,

то они называются случайными.

Случай называется благоприятным событию, если появление этого случая влечет за собой появление события. Если результаты опытов сводятся к схеме случаев, то вероятность события А вычисляется по формуле:

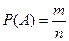(4.37),

где n – общее число случаев, m – число случаев, благоприятных событию А.

Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В.

Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и события В.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р(А+В) = Р(А) + Р(В) (4.38).

В случае, когда события А и В совместны, вероятность их суммы выражается формулой:

Р(А+В) = Р(А) + Р(В) – Р(А*В) (4.39).

Если события 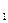А , А 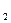, …, А 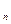несовместны и образуют полную группу, то сумма их вероятностей равна единице:

.

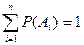Событие 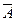называется противоположным событию А, если оно состоит в непоявлении события А. Сумма вероятностей противоположных событий равна единице:

Р(А) + Р( 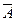) = 1 (4.40).

В число случайных событий включают и событие 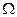, которое наблюдается в результате опыта всегда, а также событие Ǿ, которое не наблюдается в результате опыта никогда. Следовательно,

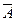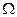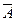А + = , А * = Ǿ

При этом 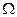называется достоверным событием, а Ǿ - невозможным событием. Очевидно, что Р( 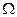) = 1, а Р(Ǿ) = 0. События А и В называются несовместными, если они не могут наступить в одном и том же опыте, т.е. АВ = Ǿ.

Если случайные события 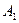, , 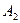…, 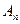попарно несовместны, то

.

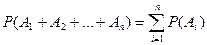Для произвольных же слагаемых:

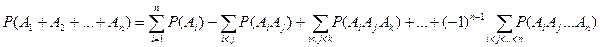
Условной вероятностью события А при наличии В называется вероятность события А, вычисленная при условии, что событие В произошло. Эта вероятность обозначается Р(А/В).

События А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий:

Р(А/В) = Р(А); Р(В/А) = Р(В) (4.41).

Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого:

Р(А*В) = Р(А) * Р(В/А) (4.42)

или

Р(А*В) = Р(В) * Р(А/В) (4.43).

Для независимых событий А и В:

Р(А*В) = Р(А) * Р(В) (4.44).

Формула полной вероятности; формула Байеса. Предположим, что случайные события 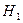, , 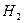…. образуют полную группу попарно несовместных событий. Тогда для всякого случайного события А:

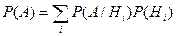(4.45).

Это – так называемая формула полной вероятности. Формула Байеса:

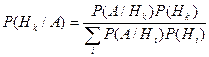(4.46).

Формула Байеса позволяет выразить условные вероятности 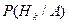рассматриваемых гипотез при условии, что произошло событие А.

Пример. В первой урне 7 белых и 3 черных шара, во второй 8 белых и 4 черных шара, в третьей 2 белых и 13 черных шаров. Из этих урн наугад выбирается одна урна и из нее наугад извлекается один шар. Какова вероятность того, что извлеченный шар окажется белым?

Решение. Обозначим буквой А событие, что из выбранной урны извлечен белый шар. Обозначим через 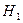, , 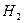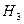гипотезы, что из данных трех урн выбрана соответственно первая, вторая и третья урны. Эти гипотезы образуют полную группу попарно несовместных событий:

.

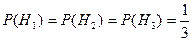Заметим, что 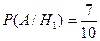, , 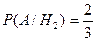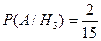. Тогда по формуле полной вероятности:

.

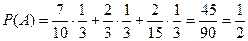4.3.2. Элементы комбинаторики.

Размещениями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения. Число размещений из n элементов по m в каждом обозначается символом 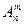и вычисляется по формуле:

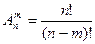(4.46).

Число размещений с повторениями равно:

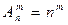(4.47).

Перестановками из n элементов называются такие соединения, из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов. Число перестановок обозначается символом :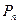

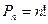(4.48).

Если же существует n элементов: a, b, …, d, среди которых элемент а повторяется 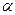раз, элемент b повторяется 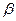раз и т. д. и 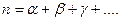, то число перестановок с повторениями выражается при помощи формулы:

Р (с повторен.) = 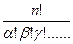(4.49).

Сочетаниями из n элементов по m в каждом называются такие соединениями, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга, по крайней мере, одним элементом. Например, из трех элементов а, в, с можно составить только одно сочетание по три элемента: авс.

Число сочетаний из n элементов по m в каждом вычисляется так:

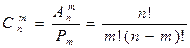(4.50).

Формула для вычисления числа сочетаний с повторениями:

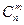(с повтор.) = 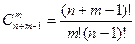(4.51).

Формула Бернулли. Когда рассматривается последовательность независимых испытаний, каждое из которых завершается наступлением (успех) или ненаступлением (неудача) случайного события А и Р(А) = p, а Р( 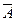) = 1- p = q, то вероятность 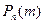того, что в n таких испытаниях произойдет ровно m успехов (событие А произойдет ровно m раз) вычисляется по формуле Бернулли:

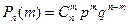(4.52).

Пример: монета бросается 3 раза. Какова вероятность, что все три раза выпадет орел?

Решение: Так как в каждом случае выпадение орла – независимое событие, то искомая вероятность Р(А*А*А) = Р(А)*Р(А)*Р(А). Следовательно, Р(А*А*А) = (1/2) * (1/2) * (1/2) = 1/ 8.

Пример: Монета бросается 2 раза. Какова вероятность того, что решка выпадет только 1 раз?

Решение: Благоприятные варианты: а) 1 ; 0 б) 0; 1. Вероятность события (а) равна ½* ½ = ¼. Вероятность события (б) ½* ½ = ¼. Общая вероятность того, что решка выпадет только 1 раз, равна сумме этих вероятностей как независимых друг от друга событий, т.е. ½.

Пример: Монета бросается 5 раз. Первые 4 раза выпала решка. Какова вероятность того, что на пятый раз выпадет тоже решка?

Решение: Так как выпадение любой стороны монеты – независимое событие, то вероятность выпадения и на пятый раз решки равна 0.5.

Пример: Независимо бросаются 2 монеты. Какова вероятность того, что среди них найдутся монеты, упавшие орлом, и монеты, упавшие решкой?

Решение: все возможные варианты: а) 1; 0 б) 0; 1; в) 1; 1 г) 0; 0. Благоприятных два варианта, поэтому искомая вероятность равна 2/4 = ½.

Пример: Имеется 10 разных облигаций. Инвестор хотел бы построить портфель из 2-х облигаций, включив каждую из них по одной штуке. Сколько вариантов портфелей может сформировать инвестор?

Решение: .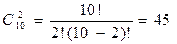

Пример: Какова вероятность того, что при бросании десяти монет выпадет семь гербов и три решки?

Решение: Здесь речь идет о десяти испытаниях Бернулли с вероятностью успеха (выпадение герба 7 раз) Р = 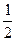и выпадения решки Р = 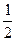(3 раза). Следовательно, по формуле Бернулли:

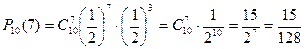
4.3.3. Свойства математического ожидания и дисперсии случайной величины.

Пусть дискретная случайная величина принимает конечное или счетное число значений. Каждому значению дискретной случайной величины отвечает его вероятность. Последовательность таких пар образует ряд распределения дискретной случайной величины. Среднее значение есть взвешенная средняя всех возможных значений случайной величины, роль весов играют вероятности.

Ожидаемое среднее значение случайной величины называется математическим ожиданием. Причина такого названия состоит в том, что среднее значение случайной величины есть оценка, которую ожидают получить. Математическое ожидание обозначается М(Х) или Е(Х).

Математическое ожидание дискретной случайной величины Х (т.е. принимающей только конечное или счетное множество значений х1, х2, … хn соответственно с вероятностями р1, р2, … рn), равно сумме произведений значений случайной величины на соответствующие им вероятности:

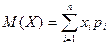(4.53).

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно этой постоянной:

М(С) = С.

2. Постоянный множитель можно выносить за знак математического ожидания:

М(СХ) = С М(Х).

3. Математическое ожидание алгебраической суммы конечного числа n случайных величин равно алгебраической сумме их математических ожиданий:

М(Х1 + Х2 + …. + Хn) = М(Х1) + М(Х2) + …. + М(Хn).

4. Математическое ожидание произведения конечного числа n независимых случайных величин равно произведению их математических ожиданий:

М(Х1 * Х2 * …. * Хn) = М(Х1) * М(Х2) * …. * М(Хn).

5. Математическое ожидание произведения двух случайных величин х1 и х2 равно сумме произведений их математических ожиданий и их ковариации:

М(Х1 * Х2) = М(Х1) * М(Х2) + cov(X1,X2).

Дисперсия случайной величины есть математическое ожидание квадрата отклонения значений случайной величины от ее математического ожидания:

D(X) = M({X – M(X)} 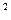) или

D(X) = M(X 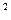) – (M(X)) .

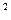Свойства дисперсии:

1. Дисперсия постоянной величины равна нулю:

D(C) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:

D(C * X) = C D(X).

3. Дисперсия суммы (разности) конечного числа n независимых случайных величин равна сумме (разности) их дисперсий:

D(Х1 + Х2 + …. + Хn) = D(Х1) + D(Х2) + …. + D(Хn).

4. Дисперсия суммы (разности) двух случайных величин Х1 и Х2 равна сумме (разности) их дисперсий и удвоенной ковариации между ними:

D(Х1 + Х2) = D(Х1) + D(Х2) + 2*cov(X1, X2).

Пример: X и Y – случайные величины. М(Х) = 2, M(Y) = 1.5.

Найти M(2*X - Y).

Ответ: 2.5.

Пример: X и Y – случайные величины. D(Х) = 2, D(Y) = 3.5. Найти D(X + Y).

Ответ: Указанных данных недостаточно, так как неизвестна ковариация между переменными X и Y (см. свойство дисперсии № 4).

Пример: Х и Y – независимые случайные величины. D(X) = 1.5, D(Y) = 2. Найти D(X+Y).

Ответ: 3.5

Пример: X – случайная величина. М(Х) = 2.5, D(X) = 1.5. Найти D(3*X + 4).

Ответ: 13.5.