Задания для самостоятельного решения
I уровень
1.1. Диагональ правильной четырехугольной призмы равна 25см, а диагональ ее боковой грани 20см. Найдите высоту призмы.
1.2. Сечение железнодорожной насыпи имеет вид трапеции, нижнее основание которой 14 м, верхнее 8 м и высота 3,2 м. Определите, сколько кубических метров земли приходится на 1 км насыпи.
1.3. В наклонной треугольной призме проведено сечение перпендикулярное боковому ребру равному 12 см. В полученном треугольнике две стороны с длинами 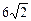 см и 8 см образуют угол 45°. Найдите площадь боковой поверхности призмы.
см и 8 см образуют угол 45°. Найдите площадь боковой поверхности призмы.
1.4. Основанием прямого параллелепипеда является ромб со стороной 4 см и острым углом 60°. Найдите диагонали параллелепипеда, если длина бокового ребра 10 см.
1.5. Основанием прямого параллелепипеда является квадрат с диагональю, равной 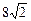 см . Боковое ребро параллелепипеда 5 см. Найдите площадь полной поверхности параллелепипеда.
см . Боковое ребро параллелепипеда 5 см. Найдите площадь полной поверхности параллелепипеда.
1.6. Основанием наклонного параллелепипеда является прямоугольник со сторонами 3 см и 4 см. Боковое ребро равное 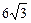 см наклонено к плоскости основания под углом 60°. Найдите объем параллелепипеда.
см наклонено к плоскости основания под углом 60°. Найдите объем параллелепипеда.
1.7. Вычислите площадь поверхности прямоугольного параллелепипеда, если два ребра и диагональ, исходящие из одной вершины, равны соответственно 11 см, 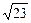 см и 13 см.
см и 13 см.
1.8. Определите вес каменной колонны, имеющей форму прямоугольного параллелепипеда, с размерами 0,3 м, 0,3 м и 2,5 м, если удельный вес материала равен 2,2 г/см3.
1.9. Найдите площадь диагонального сечения куба, если диагональ его грани равна  дм.
дм.
1.10. Найдите объем куба, если расстояние между двумя его вершинами, не лежащими в одной грани, равно 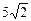 см.
см.
II уровень
2.1. Основанием наклонной призмы является равносторонний треугольник со стороной 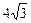 см. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите площадь сечения призмы, проходящего через боковое ребро и высоту призмы, если известно, что одна из вершин верхнего основания проектируется на середину стороны нижнего основания.
см. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите площадь сечения призмы, проходящего через боковое ребро и высоту призмы, если известно, что одна из вершин верхнего основания проектируется на середину стороны нижнего основания.
2.2. Основанием наклонной призмы является равносторонний треугольник ABC со стороной равной 3 см. Вершина A1 проектируется в центр треугольника ABC. Ребро AA1 составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности призмы.
2.3. Вычислите объем наклонной треугольной призмы, если стороны основания 7 см, 5 см и 8 см, а высота призмы равна меньшей высоте треугольника-основания.
2.4. Диагональ правильной четырехугольной призмы наклонена к боковой грани под углом 30°. Найдите угол наклона к плоскости основания.
2.5. Основанием прямой призмы является равнобедренная трапеция, основания которой равны 4 см и 14 см, а диагональ – 15 см. Две боковые грани призмы – квадраты. Найдите площадь полной поверхности призмы.
2.6. Диагонали правильной шестиугольной призмы равны 19см и 21 см. Найдите ее объем.
2.7. Найдите измерения прямоугольного параллелепипеда, у которого диагональ равна 8 дм, и она образует с боковыми гранями углы 30° и 40°.
2.8. Диагонали основания прямого параллелепипеда равны 34 см и 38 см, а площади боковых граней 800 см2 и 1200 см2. Найдите объем параллелепипеда.
2.9. Определите объем прямоугольного параллелепипеда, в котором диагонали боковых граней, выходящие из одной вершины, равны 4 см и 5 см и образуют угол в 60°.
2.10. Найдите объем куба, если расстояние от его диагонали до непересекающегося с ней ребра равно 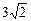 мм.
мм.
III уровень
3.1. В правильной треугольной призме проведено сечение через сторону основания и середину противоположного бокового ребра. Площадь основания 18 см2, а диагональ боковой грани наклонена к основанию под углом 60°. Найдите площадь сечения.
3.2. В основании призмы лежит квадрат ABCD, все вершины которого равноудалены от вершины A1 верхнего основания. Угол между боковым ребром и плоскостью основания равен 60°. Сторона основания 12 см. Постройте сечение призмы плоскостью, проходя через вершину C, перпендикулярно ребру AA1 и найти его площадь.
3.3. Основанием прямой призмы является равнобедренная трапеция. Площадь диагонального сечения и площади параллельных боковых граней соответственно равны 320 см2, 176 см2 и 336 см2. Найдите площадь боковой поверхности призмы.
3.4. Площадь основания прямой треугольной призмы равна 9см2, площади боковых граней 18 см2, 20 см2 и 34 см2. Найдите объем призмы.
3.5. Найдите диагонали прямоугольного параллелепипеда, зная, что диагонали его граней равны 11 см, 19 см и 20 см.
3.6. Углы, образованные диагональю основания прямоугольного параллелепипеда со стороной основания и диагональю параллелепипеда, равны соответственно a и b. Найдите площадь боковой поверхности параллелепипеда, если его диагональ равна d.
3.7. Площадь того сечения куба, которое представляет собой правильный шестиугольник, равна 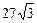 см2. Найдите площадь поверхности куба.
см2. Найдите площадь поверхности куба.
3.8. Измерения одного прямоугольного параллелепипеда относятся, как 3:5:6, а измерения второго – как 3:6:7. Зная, что их площади полных поверхностей относятся, как 7:9, найдите отношения объемов.
3.9. Основанием наклонного параллелепипеда является ромб со стороной равной b и углом в 60°. Боковое ребро также равно b и образует с прилежащими сторонами основания углы по 45°. Найдите объем параллелепипеда.
Дата добавления: 2017-09-19; просмотров: 1365;
