Задания для самостоятельного решения
I уровень
1.1. Через точку проведите прямую перпендикулярную двум заданным скрещивающимся прямым.
1.2. Определите, сколько различных плоскостей можно провести:
1) через три различные точки;
2) через четыре различные точки, никакие три из которых не лежат на одной плоскости?
1.3. Через вершины треугольника АВС, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А1, В1, С1. Докажите равенство треугольников АВС и А1В1С1.
1.4. Из вершины А прямоугольника ABCD восставлен перпендикуляр АМ к его плоскости.
1) докажите, что треугольники MBC и MDC – прямоугольные;
2) укажите среди отрезков MB, MC, MD и MA отрезок наибольшей и наименьшей длины.
1.5. Грани одного двугранного угла соответственно параллельны граням другого. Определите, какова зависимость между величинами этих двугранных углов.
1.6. Найдите величину двугранного угла, если расстояние от точки, взятой на одной грани, до ребра в 2 раза больше расстояния от точки до плоскости второй грани.
1.7. Из точки, отстоящей от плоскости на расстояние 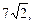 проведены две равные наклонные, образующие угол 60º. Проекции наклонных взаимно перпендикулярны. Найдите длины наклонных.
проведены две равные наклонные, образующие угол 60º. Проекции наклонных взаимно перпендикулярны. Найдите длины наклонных.
1.8. Из вершины В квадрата ABCD восставлен перпендикуляр ВЕ к плоскости квадрата. Угол наклона плоскости треугольника АСЕ к плоскости квадрата равен j, сторона квадрата равна а. Найдите площадь треугольника АСЕ.
II уровень
2.1. Через точку, которая не принадлежит ни одной из двух скрещивающихся прямых, проведите прямую, пересекающую обе данные прямые.
2.2. Параллельные прямые а, b и с не лежат в одной плоскости. Через точку А на прямой а проведены перпендикуляры к прямым b и с, пересекающие их соответственно в точках В и С. Докажите, что прямая ВС перпендикулярна прямым b и с.
2.3. Через вершину А прямоугольного треугольника АВС проведена плоскость, параллельная ВС. Катеты треугольника АС = 20 см, ВС = 15 см. Проекция одного из катетов на плоскость равна 12 см. Найдите проекцию гипотенузы.
2.4. В одной из граней двугранного угла, равного 30º, расположена точка М. Расстояние от нее до ребра угла равно 18 см. Найдите расстояние от проекции точки М на вторую грань до первой грани.
2.5. Концы отрезка АВ принадлежат граням двугранного угла, равного 90º. Расстояние от точек А и В до ребра равны соответственно АА1 = 3 см, ВВ1 = 6 см, расстояние между точками на ребре 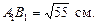 Найдите длину отрезка АВ.
Найдите длину отрезка АВ.
2.6. Из точки, отстоящей от плоскости на расстояние а, проведены две наклонные, образующие с плоскостью углы 45º и 30º, а между собой угол – 90º. Найдите расстояние между основаниями наклонных.
2.7. Стороны треугольника равны 15 см, 21 см и 24 см. Точка М удалена от плоскости треугольника на 73 см и находится на одинаковом расстоянии от его вершин. Найдите это расстояние.
2.8. Из центра О окружности, вписанной в треугольник АВС, к плоскости треугольника восставлен перпендикуляр ОМ. Найдите расстояние от точки М до сторон треугольника, если АВ = ВС = 10 см, АС = 12 см, ОМ = 4 см.
2.9. Расстояния от точки М до сторон и вершины прямого угла соответственно равны 4 см, 7 см и 8 см. Найдите расстояние от точки М до плоскости прямого угла.
2.10. Через основание АВ равнобедренного треугольника АВС проведена плоскость под углом b к плоскости треугольника. Вершина С удалена от плоскости на расстояние а. Найдите площадь треугольника АВС, если основание АВ равнобедренного треугольника равно его высоте.
III уровень
3.1. Макет прямоугольника ABCD со сторонами а и b перегнут по диагонали BD так, что плоскости треугольников BAD и BCD стали взаимно перпендикулярны. Найдите длину отрезка АС.
3.2. Две прямоугольные трапеции с углами в 60º лежат в перпендикулярных плоскостях и имеют большее общее основание. Большие боковые стороны равны 4 см и 8 см. Найдите расстояние между вершинами прямых и вершинами тупых углов трапеций, если вершины их острых углов совпадают.
3.3.Задан куб ABCDA1B1C1D1. Найдите угол между прямой CD1 и плоскостью BDC1.
3.4. На ребре АВ куба ABCDA1B1C1D1 взята точка Р – середина этого ребра. Постройте сечение куба плоскостью, проходящей через точки C1PD и найдите площадь этого сечения, если ребро куба равно а.
3.5. Через сторону AD прямоугольника ABCD проведена плоскость a так, что диагональ BD составляет с этой плоскостью угол 30º. Найдите угол между плоскостью прямоугольника и плоскостью a, если АВ = а, AD = b. Определите, при каком соотношении а и b задача имеет решение.
3.6. Найдите геометрическое место точек, равноудаленных от прямых, определенных сторонами треугольника.
Дата добавления: 2017-09-19; просмотров: 796;
