Призма. Параллелепипед
Призмой называется многогранник, две грани которого – равные n-угольники (основания), лежащие в параллельных плоскостях, а остальные n граней – параллелограммы (боковые грани). Боковым ребром призмы называется сторона боковой грани, не принадлежащая основанию.
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой призмой (рис. 1). Если боковые ребра не перпендикулярны плоскостям оснований, то призма называется наклонной. Правильной призмой называется прямая призма, основания которой – правильные многоугольники.
Высотой призмы называется расстояние между плоскостями оснований. Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани. Диагональным сечением называется сечение призмы плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Перпендикулярным сечением называется сечение призмы плоскостью, перпендикулярной боковому ребру призмы.
 Площадью боковой поверхности призмы называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех граней призмы (т.е. сумма площадей боковых граней и площадей оснований).
Площадью боковой поверхности призмы называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех граней призмы (т.е. сумма площадей боковых граней и площадей оснований).
Рис. 1
Для произвольной призмы верны формулы:
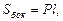
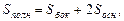
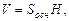 (1)
(1)
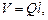
где l – длина бокового ребра;
H – высота;
P – периметр перпендикулярного сечения;
Q – Площадь перпендикулярного сечения;
Sбок – площадь боковой поверхности;
Sполн – площадь полной поверхности;
Sосн – площадь оснований;
V – объем призмы.
Для прямой призмы верны формулы:
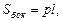
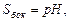
где p – периметр основания;
l – длина бокового ребра;
H – высота.
Параллелепипедом называется призма, основанием которой служит параллелограмм. Параллелепипед, у которого боковые ребра перпендикулярны к основаниям, называется прямым (рис. 2). Если боковые ребра не перпендикулярны основаниям, то параллелепипед называется наклонным. Прямой параллелепипед, основанием которого является прямоугольник, называется прямоугольным. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. Длины ребер, исходящих из одной вершины, называются измерениями параллелепипеда. Так как параллелепипед – это призма, то основные его элементы определяются аналогично тому, как они определены для призм.
Теоремы.
1. Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
2. В прямоугольном параллелепипеде квадрат длины диагонали равен сумме квадратов трех его измерений: 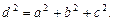
3.  Все четыре диагонали прямоугольного параллелепипеда равны между собой.
Все четыре диагонали прямоугольного параллелепипеда равны между собой.
Рис. 2
Для произвольного параллелепипеда верны формулы:
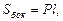
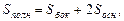
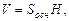
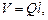
где l – длина бокового ребра;
H – высота;
P – периметр перпендикулярного сечения;
Q – Площадь перпендикулярного сечения;
Sбок – площадь боковой поверхности;
Sполн – площадь полной поверхности;
Sосн – площадь оснований;
V – объем призмы.
Для прямого параллелепипеда верны формулы:
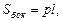
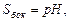 (2)
(2)
где p – периметр основания;
l – длина бокового ребра;
H – высота прямого параллелепипеда.
Для прямоугольного параллелепипеда верны формулы:
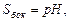
 (3)
(3)
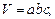
где p – периметр основания;
H – высота;
d – диагональ;
a,b,c – измерения параллелепипеда.
Для куба верны формулы:
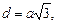

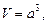
где a – длина ребра;
d – диагональ куба.
Пример 1.Диагональ прямоугольного параллелепипеда равна 33 дм, а его измерения относятся, как 2 : 6 : 9. Найти измерения параллелепипеда.
Решение. Для нахождения измерений параллелепипеда воспользуемся формулой (3), т.е. тем фактом, что квадрат гипотенузы прямоугольного параллелепипеда равен сумме квадратов его измерений. Обозначим через k коэффициент пропорциональности. Тогда измерения параллелепипеда будут равны 2k, 6k и 9k. Запишем формулу (3) для данных задачи:
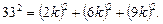
Решая это уравнение относительно k, получим:


Значит, измерения параллелепипеда равны 6 дм, 18 дм и 27 дм.
Ответ: 6 дм, 18 дм, 27 дм.
Пример 2. Найти объем наклонной треугольной призмы, основанием которой служит равносторонний треугольник со стороной 8 см, если боковое ребро равно стороне основания и наклонено под углом 60º к основанию.
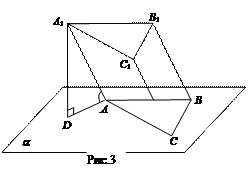 Решение. Сделаем рисунок (рис. 3).
Решение. Сделаем рисунок (рис. 3).
Для того, чтобы найти объем наклонной призмы необходимо знать площадь ее основания и высоту. Площадь основания данной призмы – это площадь равностороннего треугольника со стороной 8 см. Вычислим ее:
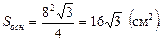
Высотой призмы является расстояние между ее основаниями. Из вершины А1 верхнего основания опустим перпендикуляр на плоскость нижнего основания А1D. Его длина и будет высотой призмы. Рассмотрим DА1АD: 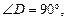
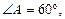 так как это угол наклона бокового ребра А1А к плоскости основания, А1А = 8 см. Из этого треугольника находим А1D:
так как это угол наклона бокового ребра А1А к плоскости основания, А1А = 8 см. Из этого треугольника находим А1D:

Теперь вычисляем объем по формуле (1):
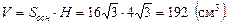
Ответ: 192 см3.
Пример 3. Боковое ребро правильной шестиугольной призмы равно 14 см. Площадь наибольшего диагонального сечения равна 168 см2. Найти площадь полной поверхности призмы.
Решение. Сделаем рисунок (рис. 4)
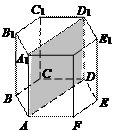
Рис. 4
Наибольшее диагональное сечение – прямоугольник AA1DD1, так как диагональ AD правильного шестиугольника ABCDEF является наибольшей. Для того, чтобы вычислить площадь боковой поверхности призмы, необходимо знать сторону основания и длину бокового ребра.
Зная площадь диагонального сечения (прямоугольника), найдем диагональ основания.
Поскольку 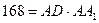 , то
, то 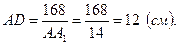
Так как 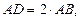 то АВ = 6 см.
то АВ = 6 см.
Тогда периметр основания равен: 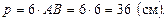
Найдем площадь боковой поверхности призмы:
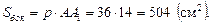
Площадь правильного шестиугольника со стороной 6 см равна:
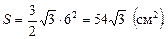
Находим площадь полной поверхности призмы:
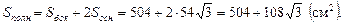
Ответ: 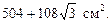
Пример 4. Основанием прямого параллелепипеда служит ромб. Площади диагональных сечений 300 см2 и 875 см2. Найти площадь боковой поверхности параллелепипеда.
Решение. Сделаем рисунок (рис. 5).

Обозначим сторону ромба через а, диагонали ромба d1 и d2, высоту параллелепипеда h. Чтобы найти площадь боковой поверхности прямого параллелепипеда необходимо периметр основания умножить на высоту:  (формула (2)). Периметр основания р = АВ + ВС + CD + DA = 4AB = 4a, так как ABCD – ромб. Н = АА1 = h. Т.о.
(формула (2)). Периметр основания р = АВ + ВС + CD + DA = 4AB = 4a, так как ABCD – ромб. Н = АА1 = h. Т.о. 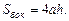 Необходимо найти а и h.
Необходимо найти а и h.
Рассмотрим диагональные сечения. АА1СС1 – прямоугольник, одна сторона которого диагональ ромба АС = d1, вторая – боковое ребро АА1 = h, тогда
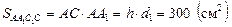
Аналогично для сечения ВВ1DD1 получим:
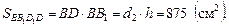
Используя свойство параллелограмма такое, что сумма квадратов диагоналей равна сумме квадратов всех его сторон, получим равенство 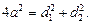 Получим следующее:
Получим следующее:
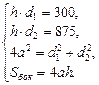
Из первых двух равенств выразим 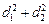 и подставим в третье. Получим:
и подставим в третье. Получим:
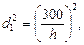
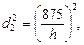

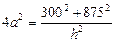 и далее
и далее
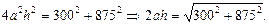 Тогда
Тогда
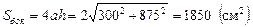
Ответ: 1850 см2.
Пример 5. На ребрах СС1, AD и АВ куба ABCDA1B1C1D1 взяты соответственно точки Р, М, R – середина этих ребер. Построить сечение куба плоскостью, проходящей через точки Р, М, R. Считая ребро куба равным 24 см, найти площадь полученного сечения.
Решение. Сделаем рисунок (рис. 6).

Построение. Прямая MR – след секущей плоскости на плоскости нижнего основания. 
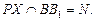
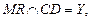
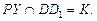 Получается искомое сечение куба PNRMK. Для вычисления его площади воспользуемся теоремой о площади ортогональной проекции многоугольника на плоскость. Многоугольник PNRMK, его ортогональная проекция – СВRMD, определим, где угол между плоскостями этих многоугольников. Ребром двугранного угла является прямая MR. Из точки Р опустим перпендикуляр на прямую MR:
Получается искомое сечение куба PNRMK. Для вычисления его площади воспользуемся теоремой о площади ортогональной проекции многоугольника на плоскость. Многоугольник PNRMK, его ортогональная проекция – СВRMD, определим, где угол между плоскостями этих многоугольников. Ребром двугранного угла является прямая MR. Из точки Р опустим перпендикуляр на прямую MR: 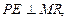 точка Е – середина отрезка MR.
точка Е – середина отрезка MR. 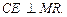
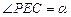 – угол между плоскостью многоугольника и его проекции. Теорему запишем в виде:
– угол между плоскостью многоугольника и его проекции. Теорему запишем в виде:
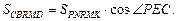 Тогда
Тогда 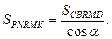
Вычислим 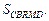 Так как ABCD – квадрат, а
Так как ABCD – квадрат, а 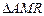 – треугольник равнобедренный
– треугольник равнобедренный 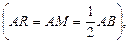 то
то
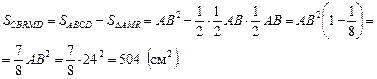
Вычислим 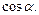

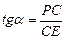 из
из 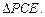
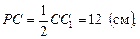
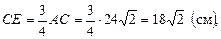
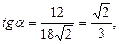
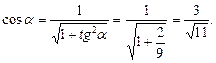
Площадь сечения: 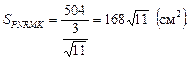
Ответ: 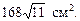
Дата добавления: 2017-09-19; просмотров: 1953;
