Описание задачи и пример ее решения
А. Описание задачи
Вентилятор комнатного кондиционера управляется встроенным программно-аппаратным блоком, работающим на базе нечетких множеств.
Основу программной реализации составляют три экспертных правила, определяющие зависимость скорости вращения вентилятора V от температуры воздуха в помещении t.
1. ЕСЛИ t = «низкая», ТО V = «низкая».
2. ЕСЛИ t = «средняя», ТО V = «средняя».
3. ЕСЛИ t = «высокая», ТО V = «высокая».
Данные правила определяют две лингвистические переменные:
· температура воздуха в помещении t Î {«низкая», «средняя», «высокая»};
· скорость вращения вентилятора V Î {«низкая», «средняя», «высокая»}.
Для каждого качественного значения каждой лингвистической переменной экспертным путем определены нечеткие множества. При этом температура воздуха в комнате может варьироваться от 0 до 60 °С,
а скорость вращения вентилятора – от 0 до 1000 об/мин (рис. 35).
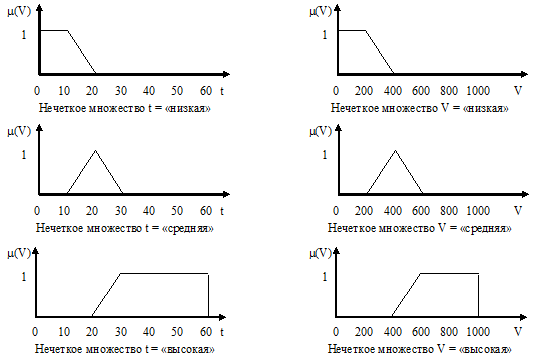
Рис. 35. Нечеткие множества для лингвистических переменных t и V
Предположим, что датчик кондиционера определил температуру воздуха в помещении, равную 22 °C. Процедура определения скорости вращения вентилятора выглядит следующим образом.
Этап 1. В левых частях правил указаны три нечетких множества, заданных на интервале t. Определенные значения функции принадлежности: mTнизкая(22) = 0, mTсредняя(22) = 0,8 и mTвысокая(22) = 0,2.
Этап 2. Полученные значения используются для модификации нечетких множеств правых частей методом «умножения» (рис. 36).
| h XK9tu+4/Bcz9/XgO4+MPlukPAAAA//8DAFBLAwQUAAYACAAAACEAC86jsN8AAAAIAQAADwAAAGRy cy9kb3ducmV2LnhtbEyPQUvDQBCF74L/YRnBm90kJTXGbEop6qkItoJ4m2anSWh2NmS3SfrvXU96 HN7He98U69l0YqTBtZYVxIsIBHFldcu1gs/D60MGwnlkjZ1lUnAlB+vy9qbAXNuJP2jc+1qEEnY5 Kmi873MpXdWQQbewPXHITnYw6MM51FIPOIVy08kkilbSYMthocGetg1V5/3FKHibcNos45dxdz5t r9+H9P1rF5NS93fz5hmEp9n/wfCrH9ShDE5He2HtRKcgXT0GUsFTAiLEyyxNQRwDl2QRyLKQ/x8o fwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0Nv bnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAA AC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQAco9GvFwMAAPgMAAAOAAAAAAAAAAAAAAAA AC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQALzqOw3wAAAAgBAAAPAAAAAAAAAAAA AAAAAHEFAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAfQYAAAAA "> 1 * 0,8 = 0 200 400 600 800 1000 |
0 200 400 600 800 1000 | |
| 1 * 0,2 = 0 200 400 600 800 1000 |
0 200 400 600 800 1000 |
Рис. 36. Модификация нечетких множеств
| |
Этап 4. Скалярное значение суперпозиции соответствует координате центра тяжести на базовой шкале. Для ее определения фигуру, указанную на рис. 37, необходимо разбить на элементарные треугольники и прямоугольники (рис. 38), определение центров тяжести которых не составляет труда.
| 0,8 |
| 0,2 |
| F1 |
| F3 |
| F2 |
0 200 400 600 800 1000
Рис. 38. Разбиение на элементарные фигуры
Геометрически центр тяжести треугольника находится на пересечении медиан, прямоугольника – диагоналей. Математически координаты центра тяжести этих фигур определяются по следующим формулам:
а) треугольника:
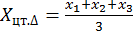 ;
; 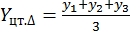 ;
;
б) прямоугольника:
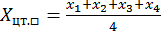 ;
; 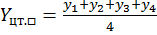 ,
,
где xi и yi – координаты i-й вершины треугольника (прямоугольника).
Координаты третьей вершины треугольника F2 можно определить, исходя из подобия треугольников.
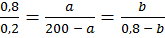 .
.
Рис. 39. Схема для определения координат третьей вершины треугольника
Из соотношения получаем: а = 160 и b = 0,64. Таким образом, x3 = 560 и y3 = 0,16.
Координаты центров тяжести фигур:
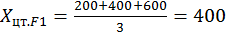 ;
; 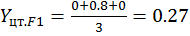 ;
;
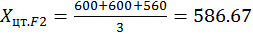 ;
;  ;
;
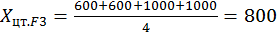 ;
; 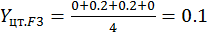 .
.
Центр тяжести суперпозиции определяется как средневзвешенная величина по формулам:
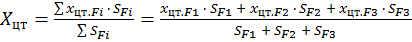 ;
;
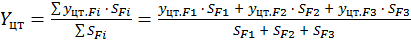 ;
;
где SFi – площадь i-й фигуры.
Площади фигур:
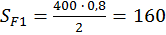 ;
;
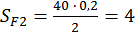 ;
;
 .
.
Центр тяжести суперпозиции:
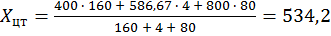 ;
;
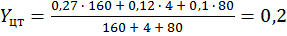 .
.
Таким образом, скорость вращения вентилятора при t = 22 °C должна быть V = Xцт = 534,2 об/мин.
Дата добавления: 2017-09-19; просмотров: 544;
