Описание задачи и пример ее решения
А. Описание задачи
Целевая функция задана выражением f(x) = 25 + 10x – 46x2 + x3. Требуется найти максимальное и минимальное значение целевой функции в интервале x Î [-10, 53].
Б. Решение с помощью математического анализа (точный метод решения оптимизационных задач)
Очевидно, что данную задачу можно решить с помощью методов математического анализа. Последовательность решения выглядит следующим образом.
1. Определение первой производной: f’(x) = 10 – 92x + 3x2.
2. Определение корней квадратного уравнения 10 – 92x + 3x2 = 0: x1 = 30.558, x2 = 0.109.
3. Определение второй производной: f”(x) = –92 + 6x.
4. Определение типа экстремумов:
· f”(30.558) = –92 + 6 × 30.558 = 91.348 > 0 ® минимум;
· f”(0.109) = –92 + 6 × 0.109 = –91.348 < 0 ® максимум.
5. Определение значений функции в точках экстремумов:
· f(30.558) = 25 + 10 × 30.558 – 46 × 30.5582 + 30.5583 = -14089;
· f(0.109) = 25 + 10 × 0.109 – 46 × 0.1092 + 0.1093 = 25.5.
6. Определение значений функции на границах интервала:
· f(-10) = 25 + 10 × (-10) – 46 × (-10)2 + (-10)3 = -5675;
· f(53) = 25 + 10 × 53 – 46 × 532 + 533 = 20218.
7. Определение максимального и минимального значений целевой функции:
· максимум: ymax = MAX(-14089, 25.5, -5675, 20218) = 20218 при
x = 53;
· минимум: ymin = MIN(-14089, 25.5, -5675, 20218) = -14089 при
x = 0.56.
Результаты расчетов подтверждаются графиком функции рис. 41.
В. Решение с помощью генетического алгоритма (эвристический метод решения оптимизационных задач)
Несмотря на то, что точное решение может быть легко найдено методами математического анализа, ниже приводится решение задачи с помощью генетического алгоритма на примере одной итерации вычисления максимального значения целевой функции.
Вариант решения задачи (особь) можно представить в виде битовой строки, которая будет соответствовать целочисленному значению x в заданном интервале. Таким образом, ген – это отдельный бит строки, хромосома – последовательность из 6 битов, генотип состоит из одной хромосомы (генотип Û хромосома), фенотип – десятичное представление битовой строки минус 10.
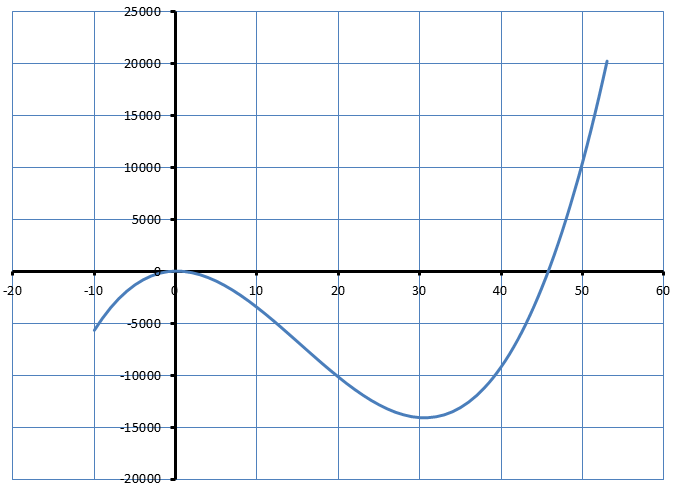
Рис. 41. График функции f(x) = 25 + 10x – 46x2 + x3 в интервале x Î [-10, 53]
Пусть размер популяции будет 4 особи, число скрещиваний – 2, число мутаций – 1 потомок на поколение. Процесс мутации заключается в инверсии одного из битов строки, выбираемого случайно.
1. Случайным образом генерируются особи исходной популяции
(табл. 11).
Таблица 11
Исходная популяция
| № | Представление особи | Фенотип, x | Значение целевой функции, f(x) = a + bx + cx2 + dx3 | |
| битовое | десятичное | |||
| -8186 | ||||
| -12407 | ||||
| -6 | -1355 | |||
2. Первая итерация – оператор скрещивания. Для скрещивания случайным образом выбраны две пары особей (1, 2) и (2, 4). В каждой паре разбиение на подстроки происходит независимо от другой пары и случайным образом. Потомки получаются в результате объединения левой подстроки одного родителя с правой подстрокой другого (табл. 12).
Таблица 12
Дата добавления: 2017-09-19; просмотров: 591;
