Распознавание образов
Распознавание образов – научное направление, связанное с разработкой принципов и построением систем, предназначенных для определения принадлежности объекта к одному из классов объектов [6]. Классы объектов могут быть заранее выделены (задача классификации) или необходимо их выявить в процессе решения задачи (задача кластеризации). При этом под объектами могут пониматься не только осязаемые органами чувств различные предметы, но и явления, процессы, ситуации, сигналы и т. п.
Одним из наиболее эффективных и распространенных способов решения задач распознавания образов являются искусственные нейронные сети. Искусственная нейронная сеть – математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей.
Базовым элементом искусственных нейронных систем является искусственный нейрон. Его обобщенная математическая модель выглядит следующим образом (рис. 42) [1].
|
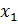
|
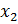
|
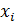
|
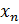
|
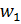
|
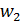
|
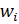
|
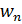
|
| f(P) |
Рис. 42. Математическая модель нейрона: входные сигналы 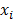 – данные, поступающие из окружающей среды или от других активных нейронов; вещественные весовые коэффициенты
– данные, поступающие из окружающей среды или от других активных нейронов; вещественные весовые коэффициенты 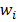 – определяют силу связи между нейронами; уровень активации (потенциал) нейрона
– определяют силу связи между нейронами; уровень активации (потенциал) нейрона 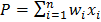 ; функция активации f(P) – предназначена для вычисления выходного значения сигнала, передаваемого другим нейронам
; функция активации f(P) – предназначена для вычисления выходного значения сигнала, передаваемого другим нейронам
Искусственная нейронная сеть состоит из нескольких слоев, в которые группируются нейроны (рис. 43).
На нейроны входного слоя подаются измеренные и преобразованные значения характеристик объекта (образа). Сигналы, поступившие к нейронам входного слоя, передаются на следующий слой (скрытый или выходной) без преобразования (т. е. к ним не применяется функция активации). Скрытые слои и выходной слой, отражающие специфику знаний, преобразуют входные данные. Выходной слой генерируют скаляр (одно значение) или вектор (несколько значений), являющийся решением задачи.
| Вектор входных сигналов | Входной слой | Скрытый слой | Скрытый слой | Выходной слой | Вектор выходных сигналов |
Рис. 43. Искусственная нейронная сеть с прямыми связями
В зависимости от количества преобразующих слоев (скрытых и выходного) различают одно- (в сети отсутствуют скрытые слои) и многослойные сети.
В качестве функций активации используются различные функциональные зависимости: линейная, пороговая, гиперболический тангенс, арктангенс, гауссиана и т. д. Одной из наиболее распространенных является сигмоидальная функция:
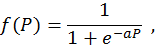
где a – коэффициент; e – основание натурального логарифма.
В зависимости от типа межнейронных связей различают искусственные нейронные сети:
· с прямыми связями (см. рис. 43);
· с перекрестными связями (рис. 44);
Рис. 44. Искусственная нейронная сеть с перекрестными связями
· с обратными (рекуррентными) связями (рис. 45). В таких сетях нейрон может посылать сигналы сам себе, нейронам того же слоя или нейронам предыдущих слоев.
Рис. 45. Искусственная нейронная сеть с обратными связями
Процедура построения искусственных нейронных сетей, используемых в задачах классификации, включает в себя насколько этапов.
Этап 1. Определение типа распознаваемых образов (фотография, видео, совокупность числовых характеристик и т. п.), набора измеряемых параметров образов, информативных с точки зрения распознавания, и классов распознаваемых образов.
Этап 2. Выбор способа преобразования (применение фильтров, подавление шумов, сегментация и т. п.) измеряемых параметров образов во входной вектор числовых величин и представления набора классов образов в виде вектора выходных величин. Эффективность нейросетевой модели повышается, если диапазоны изменения величин входного и выходного векторов будут нормализованы, например, в диапазоне [0,1] или [-1,1].
Этап 3. Проектирование архитектуры искусственной нейронной сети:
· определение количества слоев. В сети должно быть, как минимум, два слоя: входной и выходной. Количество скрытых слоев определяется, как правило, экспертным или опытным путем;
· определение количества нейронов в каждом слое. Количество нейронов во входном слое соответствует количеству преобразованных измеряемых параметров распознаваемых образов. Количество нейронов в выходном слое, как правило, соответствует количеству классов распознаваемых образов. Определение количества нейронов в каждом скрытом слое является неформальной проблемой, при решении которой можно использовать эвристическое правило: число нейронов в следующем слое должно быть в два раза меньше, чем в предыдущем;
· выбор типа связей между нейронами. Зависит от специфики решаемой задачи;
· выбор функции активации. Зависит от специфики решаемой задачи.
Этап 4. Обучение сети – уточнение значений весовых коэффициентов связей на основе многократного прогона обучающих примеров через сеть. Каждому обучающему примеру (образу) соответствуют строго определенные вектора входных и выходных величин. Обучающие примеры, как правило, представляют собой эталонные (идеальные) представления образов, а также их незначительные модификации. Они должны быть подобраны для каждого класса образов. Существует эмпирическое правило, которое устанавливает рекомендуемое соотношение l между количеством обучающих примеров и числом связей в нейронной сети: l ≤ 10 [7].
Этап 5. Тестирование сети с помощью контрольного набора примеров (образов) для оценки качества выбранной архитектуры и степени обучения. Контрольный набор должен содержать, как минимум, по одному примеру для каждого класса образов и включать в себя как эталонные, так и значительно искаженные образы.
Этапы с третьего по пятый могут совместно применяться для уточнения архитектуры сети на основе конструктивного или деструктивного подхода. В соответствии с первым подходом обучение начинается на сети небольшого размера, который постепенно увеличивается до достижения требуемой точности по результатам тестирования. Деструктивный подход базируется на принципе «прореживания дерева», в соответствии с которым из сети с заведомо избыточным объемом постепенно удаляют «лишние» слои, нейроны и примыкающие к ним связи. Этот подход дает возможность исследовать влияние удаляемых элементов на точность распознавания сети.
Процедура обучения является одной из ключевых при разработке и настройке сети. Существует большое количество подходов (правил) и соответствующих им методов (алгоритмов) обучения:
· правило коррекции по ошибке (дельта-правило);
· правило обратного распространения ошибки;
· синхронное обучение (правило Хебба);
· конкурентное обучение (правило Кохонена);
· правило Больцмана;
· и т. д.
Применение того или иного правила (алгоритма) зависит от выбранной архитектуры нейронной сети (количество слоев, тип связей, функция активации и т. п.).
Для решения задачи принадлежности предъявленного образа одному из заранее выделенных классов образов хорошо себя зарекомендовали многослойные нейронные сети с прямыми связями. Самым известным и популярным методом их обучения является алгоритм обратного распространения ошибки, который является модификацией классического метода градиентного спуска. Помимо многослойности и прямых связей, дополнительное требование его применимости – функция активации должна быть дифференцируема, т. е. иметь первую производную.
Алгоритм обратного распространения ошибки подразумевает два потока сигналов (данных) при прогоне одного обучающего образа через сеть:
· прямой (от входного до выходного слоя) – распространение сигнала, соответствующего значениям входного вектора обучающего образа;
· обратный (от выходного до входного слоя) – распространение сигнала ошибки для корректировки весовых коэффициентов связей.
Блок-схема алгоритма обратного распространения ошибки показана на рис. 46 со следующими обозначениями:
· э – номер эпохи;
· о – номер обучающего образа;
· с – номер слоя;
· нс – номер нейрона в слое с;
· NЭ – количество эпох;
· NО – количество обучающих образов;
· NС – количество слоев;
· NНс – количество нейронов в слое с;
·  – вектор входных значений обучающего образа о;
– вектор входных значений обучающего образа о;
· 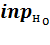 – значение элемента н входного вектора обучающего образа о;
– значение элемента н входного вектора обучающего образа о;
· 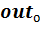 – вектор ожидаемых выходных значений обучающего образа о;
– вектор ожидаемых выходных значений обучающего образа о;
· 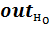 – значение элемента н выходного вектора обучающего образа о;
– значение элемента н выходного вектора обучающего образа о;
· 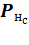 – потенциал нейрона н слоя с;
– потенциал нейрона н слоя с;
· 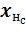 – выход нейрона н слоя с. Для нейронов входного слоя равен соответствующему элементу вектора входных значений
– выход нейрона н слоя с. Для нейронов входного слоя равен соответствующему элементу вектора входных значений 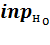 , для остальных слоев – результату расчета функции активации
, для остальных слоев – результату расчета функции активации 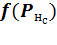 ;
;
· 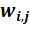 – весовой коэффициент связи нейрона i предыдущего слоя и нейрона j последующего слоя;
– весовой коэффициент связи нейрона i предыдущего слоя и нейрона j последующего слоя;
· 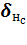 – ошибка (сигнал ошибки) нейрона н слоя с;
– ошибка (сигнал ошибки) нейрона н слоя с;
· 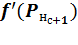 – результат расчета первой производной функции активации нейрона н слоя с+1;
– результат расчета первой производной функции активации нейрона н слоя с+1;
· 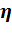 – норма обучения.
– норма обучения.
Перед процедурой обучения весовые коэффициенты всех связей инициализируются случайными малыми значениями (например, в диапазоне [-0.3, 0.3]).
| Начало |
Инициализация весовых коэффициентов всех связей сети случайными значениями 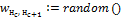
|
Для каждой эпох 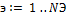
|
Для каждого обучающего образа 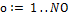
|
Инициализация (чтение) входного  и выходного и выходного 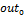 векторов образа векторов образа
|
Присвоение значений входного вектора нейронам первого слоя 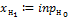
|
Для каждого последующего слоя 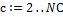 Для каждого последующего слоя
Для каждого последующего слоя 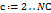
|
Для каждого нейрона слоя 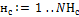 Для каждого нейрона слоя
Для каждого нейрона слоя 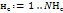
|
Расчет потенциала по всем входящим связям нейрона 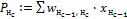 Расчет потенциала по всем входящим связям нейрона
Расчет потенциала по всем входящим связям нейрона 
|
Расчет выхода нейрона 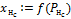 Расчет выхода нейрона
Расчет выхода нейрона 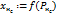
|
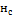
|

|
Для каждого нейрона последнего слоя 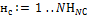 Для каждого нейрона последнего слоя
Для каждого нейрона последнего слоя 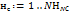
|
Расчет ошибки 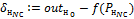
|
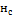
|
Для каждого промежуточного слоя 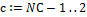 Для каждого последующего слоя
Для каждого последующего слоя 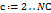
|
Для каждого нейрона слоя 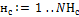 Для каждого нейрона слоя
Для каждого нейрона слоя 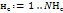
|
Расчет ошибки по всем исходящим связям нейрона  Расчет ошибки
Расчет ошибки 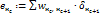
|
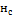
|

|
Коррекция весовых коэффициентов всех связей сети 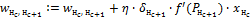
|

|

|
| Конец |
Рис. 46. Блок-схема алгоритма обратного распространения ошибки
При прогоне через сеть одного обучающего образа выполняется коррекция весовых коэффициентов. Прогон всех обучающих образов называется эпохой. Для настройки весовых коэффициентов (обучения) сети должно пройти достаточно большое количество эпох (несколько сотен, тысяч и т. п. – в зависимости от масштабов сети). Количество эпох может быть определено автоматически по заданной максимальной разнице средней ошибки (погрешности) между текущей эпохой и предыдущей, задано экспертом (как на рис. 46) и т. п.
При прямом распространении сигнала выполняется стандартная процедура, как и при распознавании образа:
· нейронам первого (входного) слоя присваиваются значения входного вектора  без преобразования. Можно условно принять, что эти значения
без преобразования. Можно условно принять, что эти значения  являются одновременно потенциалами
являются одновременно потенциалами 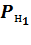 и выходами
и выходами 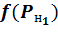 нейронов. Ввиду отсутствия преобразования при подсчете количества слоев
нейронов. Ввиду отсутствия преобразования при подсчете количества слоев
сети входной слой не учитывается и на схемах эти нейроны часто отображают иначе, чем остальные;
· для нейронов промежуточных и выходного слоев с учетом текущих значений весовых коэффициентов сети выполняется расчет потенциала 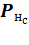 и выхода
и выхода 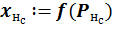 .
.
При проходе слоев в обратном направлении выполняется расчет сигнала ошибки:
· для нейронов последнего (выходного) слоя как разница между ожидаемым для образа значением выхода и полученным:
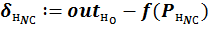 ;
;
· для нейронов промежуточных слоев с учетом весовых коэффициентов связей с нейронами последующего слоя и их сигналов ошибки:
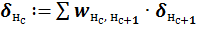 .
.
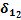
|

|
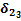
|
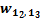
|
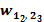
|
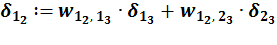 .
.
Рис. 47. Пример расчета сигнала ошибки для нейрона 1 слоя 2
Заключительной операцией является корректировка весовых коэффициентов всех связей на величину:
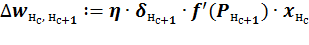 ,
,
где 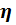 – норма обучения;
– норма обучения; 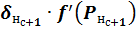 – локальный градиент. Произведение сигнала ошибки и результата расчета первой производной функции активации для нейрона, в который входит связь;
– локальный градиент. Произведение сигнала ошибки и результата расчета первой производной функции активации для нейрона, в который входит связь; 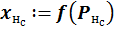 – результат расчета функции активации для нейрона, из которого выходит связь.
– результат расчета функции активации для нейрона, из которого выходит связь.
Норма обучения 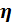 – коэффициент, от которого зависит величина изменения веса (скорость обучения). Выбирается в диапазоне 0 <
– коэффициент, от которого зависит величина изменения веса (скорость обучения). Выбирается в диапазоне 0 < 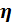 < 1.
< 1.
Значения потенциалов 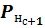 и
и 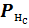 принимаются полученными при прямом распространении сигнала. В связи с этим корректировка весовых коэффициентов может выполняться независимо и в любом направлении (прямом или обратном).
принимаются полученными при прямом распространении сигнала. В связи с этим корректировка весовых коэффициентов может выполняться независимо и в любом направлении (прямом или обратном).
Дата добавления: 2017-09-19; просмотров: 1198;