Характеристика дополнительных ограничений скорости и мероприятий по их устранению
| № ограни-чения | Причина ограничения (мероприятие по устранению ограничения) | Дополни-тельные эксплуатационные расходы на проход одного поезда DCi, руб. | Потребные капвложения на устра-нение ограничения Ki, руб. | Срок окупае-мости Токi, лет | Подразде-ление, выполняющее мероприятие |
| Кривая малого радиуса R = 300 м (увеличение радиуса R = 1000 м) | 2 000 000 | 2.2 | ПМС-219 | ||
| Кривая малого радиуса R = 350 м (увеличение радиуса R = 1000 м) | 2 500 000 | 3.4 | ПМС-219 | ||
| Деформация опоры моста (укрепление опоры моста) | 3 500 000 | 4.8 | МСО-9 |
Окончание табл. 9
| № ограни-чения | Причина ограничения (мероприятие по устранению ограничения) | Дополни-тельные эксплуатационные расходы на проход одного поезда DCi, руб. | Потребные капвложения на устра-нение ограничения Ki, руб. | Срок окупае-мости Токi, лет | Подразде-ление, выполняющее мероприятие |
| Дефект трубы (замена оголовка трубы) | 4 500 000 | 4.9 | МСО-9 | ||
| Кривая малого радиуса R = 400 м (увеличение радиуса R = 1200 м) | 4 200 000 | 7.7 | ПМС-219 | ||
| Дефект трубы (замена оголовка трубы) | 5 000 000 | 10.5 | МСО-9 |
Примечание. Срок окупаемости отдельного мероприятия применительно к рассматриваемой задаче рассчитывается по формуле 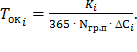
В качестве подразделений, которые могут выполнять мероприятия, выбраны:
· ПМС-219 – путевая машинная станция, выполняющая работы по земляному полотну и верхнему строению пути;
· МСО-9 – мостостроительный отряд, выполняющий работы по искусственным сооружениям.
В.Постановка задачи
Составить план (выбрать) мероприятий, направленных на устранение дополнительных ограничений скорости, чтобы капитальные вложения в мероприятия плана окупились в минимально короткий срок (принесли максимальный доход) при безусловном выполнении заданных требований на характеристики плана (решение задачи).
Срок окупаемости всего плана мероприятий рассчитывается по формуле
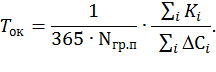
В качестве требований к характеристикам плана выступают следующие:
· суммарные капвложения не должны превышать 12 000 000 руб.;
· ПМС-219 должна освоить не менее 3 000 000 руб.;
· МСО-9 должен освоить не менее 4 500 000 руб.
Таким образом требуется найти план с минимальным сроком окупаемости
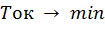
с учетом следующих условий:
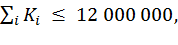 (О1)
(О1)
где i соответствует мероприятиям, включенным в план;
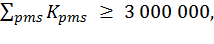 (О2)
(О2)
где pms соответствует мероприятиям, включенным в план и выполняемым ПМС-219;
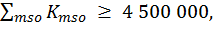 (О3)
(О3)
где mso соответствует мероприятиям, включенным в план и выполняемым МСО-9.
Г.Решение задачи методом частичного перебора
Дерево поиска решения методом частичного перебора показано на рис. 31.
Обход дерева выполняется сверху вниз слева направо (поиск в глубину). Каждый узел дерева (за исключением корневого) соответствует набору мероприятий. Mi = 1 означает включение i-го мероприятия в план,
Mi = 0 – невключение. Соответственно план мероприятий для каждого узла включает в себя все мероприятия, для которых Mi = 1, начиная с корневого и до текущего узла при спуске по стрелкам. Включение мероприятий в план согласно табл. 9 обеспечивает монотонность возрастания критерия (срока окупаемости). Надпись Oj означает несоблюдение j-го требования.
Характеристика найденного оптимального решения (плана) включает:
· мероприятия 1, 5 и 6;
· потребные капвложения менее максимально выделяемого объема 9 000 000 ≤ 12 000 000;
· объем капвложений, осваиваемых ПМС-219, не менее минимально потребного 4 500 000 ≥ 3 000 000;
· объем капвложений, осваиваемых МСО-9, не менее минимально потребного 4 500 000 ≥ 4 500 000;
· срок окупаемости плана мероприятий Tок = 3,5 года.
| | Рис. 31. Дерево поиска решения методом частичного перебора: узел с тонкой одинарной рамкой – промежуточное решение, неудовлетворяющее требованиям O2 или О3, из которого: имеет смысл дальше искать оптимальное решение (ниже расположены узлы, обозначенные большими квадратами); не имеет смысла дальше искать оптимальное решение, так как до этого уже было найдено допустимое решение с меньшим сроком окупаемости Ток (ниже расположены узлы, обозначенные малыми квадратами с одинарной штриховой рамкой). При дальнейшем поиске решения из этого узла, даже если будет найден новый допустимый вариант плана, значение срока окупаемости по нему будет заведомо хуже найденного; узел с толстой одинарной рамкой и белым фоном – допустимое, но не оптимальное решение; узел с толстой одинарной рамкой и серым фоном – оптимальное решение; узел с двойной рамкой – недопустимое решение. Нарушено требование на суммарные капвложения O1. Добавление мероприятий в такой план приведет к еще большему нарушению этого требования. Несоблюдение требований O2 и O3 (на минимальные суммарные капвложения, осваиваемые конкретными подразделениями) в отличие от требования O1 не означает прекращения поиска решения из конкретного узла; узел с одинарной штриховой рамкой – решение, не требующее рассмотрения (не попавшее в обход дерева) |
Д.Решение задачи с использованием алгоритма А*.
Дерево поиска решения с помощью алгоритма А* показано на рис. 32.
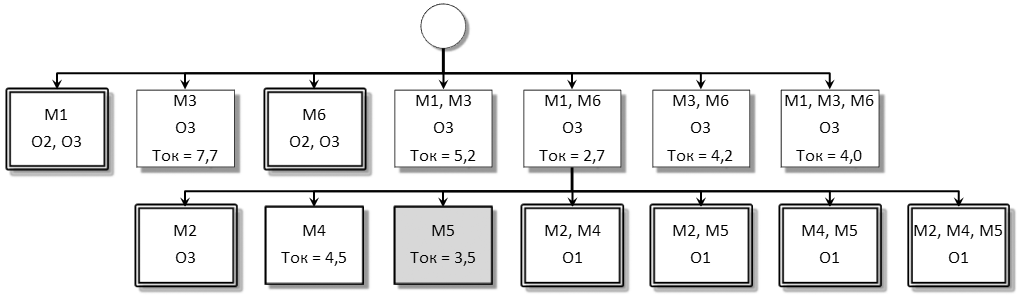
Рис. 32. Дерево при поиске решения с использованием алгоритма А*
Одним из вариантов решения задачи с использованием алгоритма А* является перебор возможных планов, когда на каждом уровне дерева рассматриваются сочетания мероприятий, выполняемые одним подразделением.
Надписи, цвет фона и тип рамки узлов приняты, как и при решении задачи методом частичного перебора. На 1-м уровне вариант плана должен обязательно отвечать требованиям O1 и O2, а на 2-м уровне – всем требованиям. В связи с этим, в узлах, несоответствующих этим требованиям, расчет критерия (срока окупаемости Ток) не выполняется.
Толстой одинарной рамкой и серым фоном выделен узел, соответствующий оптимальному плану. Результат (оптимальный план) идентичен полученному с помощью метода частичного перебора и состоит из мероприятий 1, 5 и 6.
Если бы из узла 1-го уровня с мероприятиями 1 и 6 все продолжения вели бы к узлам 2-го уровня, для каждого из которых не соблюдалось хотя бы одно требование, тогда при поиске решения следовало бы рассмотреть продолжения из следующего по оптимальности узла 1-го уровня (на рис. 32 узел с мероприятиями 1, 3 и 6) и т. д.
Следует отметить, что в данном конкретном случае алгоритм А* оказался эффективнее метода частичного перебора (при одинаковом результате потребовалось меньше вычислений). В то же время, если бы количество мероприятий, выполняемых ПМС-219, было бы не три, а десять, то уже на 1-м уровне пришлось бы рассматривать 1023 варианта вместо 7.
Дата добавления: 2017-09-19; просмотров: 645;
