Прогнозирование по диагностическим параметрам (прогнозирование по состоянию)
Прогнозирование по диагностическим параметрам — это наиболее прогрессивный вид прогнозирования, дающий более высокую точность прогноза.
Методической основой прогнозирования по диагностическим параметрам является:
— знание процессов изменения технического состояния машины (априорная информация);
— знание технического состояния машины в данный момент (диагностическая информация);
— умение эксплуатации этих процессов в будущем.
Экстраполяция — это статистический прием, посредством которого на основании определенного числа членов статистического ряда делается попытка продлить ряд за пределы данных нам известных значений ряда.
Одно из основных положений теории прогнозирования заключается в том, что вывод об изменении параметра, в частности об изменении диагностического параметра элемента машины в будущем, делается на основании изучения этого параметра в прошлом. Чем больше имеется данных об изменении параметра в прошлом, тем точнее будет осуществлен прогноз на будущее.
Может быть, два вида информации об изменении параметра:
а) для совокупности одноименных элементов;
б) для конкретного элемента.
В первом случае используется метод прогнозирования по среднему статистическому изменению параметра и среднеквадратическому отклонению этого изменения.
При наличии двух видов информации представляется возможным применить метод прогнозирования по реализации. Этот метод заключается в предсказании изменения параметра конкретного элемента с учетом его индивидуального изменения в прошлом, а также характера изменения, установленного путем анализа динамики параметра совокупности одноименных элементов.
Таким образом, при прогнозировании технического состояния машин по диагностическим параметрам используются в основном два вида прогнозирования:
— прогнозирование по среднестатистическому изменению параметра;
— прогнозирование по реализации.
8.3.1 Прогнозирование по среднестатистическому изменению параметра
Суть этого вида прогнозирования состоит в том, чтоделается предположение, что прогнозируемый параметр, характеризующий техническое состояние элемента машины (узла, агрегата, машины в целом), будет изменяться аналогично параметрам одноименных элементов из опытной партии, наблюдение за которой дали имеющуюся информацию.
Таким образом, для прогнозирования по среднестатистическому изменению параметра необходима следующая информация:
— априорная информация о среднестатистическом изменении параметра машины, в зависимости от наработки;
— текущая информация о значении прогнозируемого параметра, характеризующего техническое состояние элемента в данный момент.
Априорная информация о среднестатистическом изменении параметра может быть представлена в виде веерных кривых (см. рисунок 8.2) описываемых степенной функцией вида
S=SH+Vc·Lα,
у которых коэффициент a постоянен для всей совокупности одноименных элементов, а коэффициент Vс, характеризующий скорость изменения параметра, различен.
На рисунке 8.2 коэффициент V1c характеризует тяжелые условия эксплуатации, а V4c — самые легкие.
Графически, прогнозирование по среднестатистическому изменению параметра, сводится к следующему:
1) при диагностировании машины, определяется значение диагностического параметра – Si, при наработке Li (точка А с координатами Si и Li);
2) делается два допущения:
— допускается, что прогнозируемый параметр до текущего момента (до наработки Li) имел характер изменения аналогично кривой, на которой лежит точка А;
— допускается, что и в дальнейшем этот параметр будет иметь характер изменения аналогичный кривой с точкой А;
3) с учетом этих допущений делается предположение, что параметр элемента будет изменяться после наработки Li, по кривой на которой лежит точка А;
4) зная, по априорной информации, характер изменения кривой (зная значения коэффициентов Vс и a) определяется характер изменения параметра конкретного элемента в будущем (кривая АВ);
5) прогнозируется момент наступления отказа элемента исходя из того, что прогнозируемый параметр достигнет предельно-допустимого значения (Sпд) в точке В.
Следовательно, отказ элемента должен произойти при наработке Lотк., а остаточный ресурс при этом определится по формуле:
Lост=Lотк.-Li,
где Lост — остаточный ресурс.
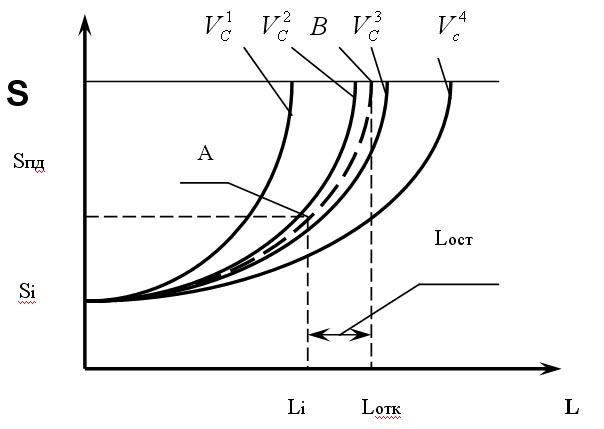
Рисунок 8.2 — Схема прогнозирования по среднестатистическому
изменению параметра
8.3.2 Прогнозирование по реализации
Это более точный вид прогнозирования, по сравнению с прогнозированием по среднестатистическому изменению параметра, но более дорогостоящий, т.к. требует большего объема информации.
Суть метода состоит в том, что прогнозирование делается на основе данных об изменении параметра конкретного элемента от его начала эксплуатации до текущего момента, а корректировка прогноза ведется с учетом информации о характере изменения параметра одноименных элементов, полученной в предыдущих исследованиях.
Таким образом, для прогнозирования по реализации необходимо систематически, через определенный интервал, проводить диагностику машины, чтобы получить данные о реальном изменении параметра элемента от начала эксплуатации до текущего момента.
8.3.3 Пример прогнозирования
Предположим, что в момент наработки L1, L2 ...Li были получены значения диагностического параметра S1, S2 ...Si (рисунок 8.3). На основе этих данных определяется конкретный вид аппроксимирующей функции. Если в качестве аппроксимирующей функции берется степенная функция вида S=SH+Vc·Lα ,то определение конкретного вида функции сводится к расчету значений коэффициентов a и Vс.
После определения функции, отображающей реальную картину изменения параметра конкретного элемента, делается предположение, что и в будущем, т.е. после наработки Li диагностический параметр S будет изменяться согласно характеру изменения данной функции (на рисунке пунктирная кривая АВ). В точке В значения данной функции достигнет предельно-допустимой величины Sпд, а, следовательно, можно предположить, что в этой точке произойдет отказ элемента.
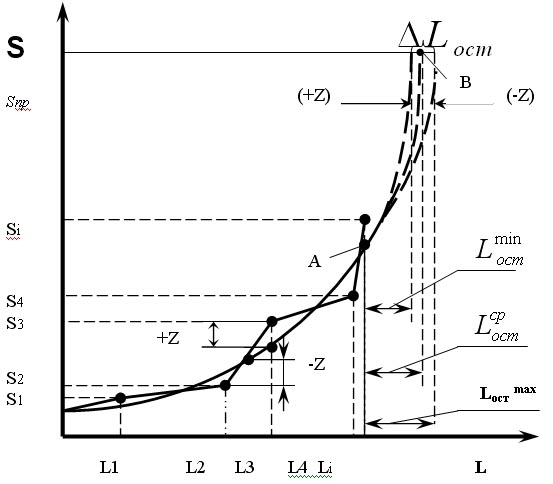
Рисунок 8.3 – Прогнозирование по реализации
Корректировка прогноза делается с целью повышения точности прогнозирования. Она осуществляется как на основе информации полученной об изменении во времени параметра конкретного элемента, так и на основе априорной информации об изменении параметра одноименных элементов.
Из приведенного примера (рисунок 8.3) видно, что реальные значения параметра S отличаются от значений теоретической кривой на величину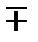 
Z. Следовательно, в данном случае общий вид аппроксимирующей функции будет:
S=SH+Vc·Lα±Z,
где Z — отклонение величины S от теоретического значения под воздействием внешних эксплуатационных факторов.
Следовательно, при прогнозировании необходимо делать допущение, что и в будущем под воздействием внешних эксплуатационных факторов параметр S может отклоняться на величину ±Z. Учет величины Z, при прогнозировании и является корректировкой прогноза.
В приведенном примере (рисунок 8.3), можно предположить, что отказ элемента произойдет в интервале наработки от Lостmin до Lостmax. Это уже прогноз, скорректированный с учетом величины Z.
Дальнейшее уточнение прогноза может вестись с учетом дополнительной информации, такой как:
— априорной информации об изменении параметра одноименных элементов после наработки Li;
— априорной информации о величине Z после наработки Li;
— информации о характере воздействия внешних эксплуатационных факторов на изменения параметра элемента после наработки Li (например: в каких природно-климатических условиях предполагается эксплуатировать машину после наработки Li) и т.д.
Из изложенного выше можно сделать вывод, что для повышения точности прогноза, необходимо увеличение объема информации, на основе которой делается прогноз.
Дата добавления: 2017-08-01; просмотров: 1967;