Процессы восстановления сложных систем и управление возрастной структурой парков
Наиболее сложно процессы восстановления проходят в больших системах, например в парках автомобилей, имеющих в своем составе автомобили разных возрастных групп (см. рисунок 2.4). При этом элементом восстанавливаемой системы (парка) является автомобиль, который поступает в парк, а затем, после определенной наработки (время, пробег), списывается или продается.
Очевидно, выбытие автомобиля можно рассматривать как отказ системы (парка), которая не может выполнить заданный объем работы, а пополнение парка – как устранение отказа восстановлением работоспособности. Изменяя соотношение поставки и списания автомобилей в парке, можно влиять на реализуемые показатели качества самого парка.
Под управлением возрастной структурой (ВС) парка понимается ее прогнозирование и такое целенаправленное изменение, которое обеспечивает получение в необходимый момент времени i заданных реализуемых показателей качества парка 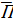 кi. В общем случае на формирование ВС парка влияют следующие основные факторы:
кi. В общем случае на формирование ВС парка влияют следующие основные факторы:
а) исходная возрастная структура, т.е. распределение парка по возрастным группам j в начальный момент i=1: а11, а12, а13,..., аij;
б) размер поставки новых автомобилей в момент i=1, 2, 3,...;
в) размер списания автомобилей Аicп.
Отношение размера поставки к размеру парка в i-м году называется коэффициентом пополнения
| ri=Aiп/Ai. | (3.14) |
Отношение размера списания к размеру парка в i-м году называется коэффициентом списания или выбытия
| bi=Aiсп/Ai. | (3.15) |
При ri=bi имеет место простое восстановление, а при ri>bi – расширенное, т.е. парк автомобилей увеличивается. При ri<bi, происходит деградация, т.е. сокращение размера парка.
На рисунке 3.7 приведена схема изменения размера образованного в момент i=t=0 парка Аi; при различном соотношении коэффициентов пополнения и списания и зафиксированном сроке службы автомобиля tсп (так называемое дискретное списание).
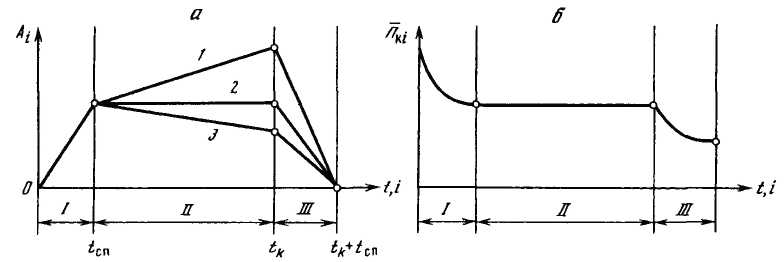
Рисунок 3.7 – Изменения размера (а) и реализуемого показателя качества (б) парка
При этом наблюдаются три характерных этапа:
I — от t=0 до t=tсп – рост парка, вызванный поставкой новых автомобилей при отсутствии списания (кроме аварийного), т.е. r>0; b=0;
II — от t=tспдо момента окончания производства (или приобретения данной фирмой) автомобилей определенной модели tк. На этом этапе в зависимости от соотношения r и b может наблюдаться относительный рост парка r>b (I, рисунок 3.7), его стабилизация r=b (2) или при r<b – сокращение (3);
III — от tкдо tк+tсппостепенная ликвидация парка данных автомобилей (r=0; b>0).
По этапам происходит изменение и реализуемых показателей качества парка (рисунок 3.7, б), в данном случае это удельный вес работоспособных автомобилей в парке, или коэффициент технической готовности αТ,
Управление ВС проводится на уровне конкретных предприятий и фирм и сводится к регулированию процессов списания-пополнения и соотношения в парке изделий разных возрастных групп при условии обеспечения требуемого (заданного) для парка объема транспортной работы при минимальных затратах или максимальной прибыли.
Методы расчета ВС парка зависят от принятого способа списания и поставки изделий:
— при дискретном списании по достижении установленного или принятого на данном предприятии срока службы tсп (1, рисунок 3.8) происходит списание или продажа автомобиля, вне зависимости от его технического состояния или показателей работы. Такая схема распространена при интенсивной эксплуатации в условиях повышенных требований к надежности (междугородные и международные перевозки, пассажирские перевозки, экстренная доставка ценных грузов и т.д.);
— случайное списание (2, рисунок 3.8) характеризуется вариацией фактической наработки до списания f(j). По этой схеме списание производится на основании контроля над определенными показателями работы автомобиля, например по накопленному расходу запасных частей, изменению производительности, уменьшению прибыли и т.д.

Рисунок 3.8 – Дискретное (1) и случайное (2) списание
3.5.1 Расчет показателей возрастной структуры парка при дискретном списании
Этот метод расчета, называемый методом диагонального сдвига, основан на следующих предпосылках (рисунок 3.9):
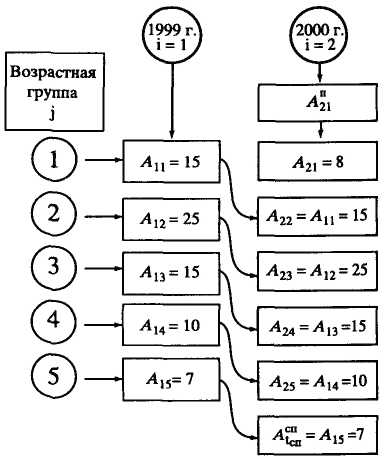
Рисунок 3.9 – Схема определения возрастной структуры парка методом
диагонального сдвига при дискретном списании
1 Различают календарное время i существования парка автомобилей данной модели и возрастную группу автомобилей j. В год образования парка или в исходный год анализа его возрастной структуры принимается i=1.
2 Возраст автомобиля j и календарное время существования данного парка i измеряются в одинаковых условных или абсолютных единицах, например годах.
3 При изменении календарного времени на одну единицу (i+1) автомобили, имевшие в момент i возраст j «стареют» на одну единицу и переходят в следующую возрастную группу (j+1), т.е. происходит диагональный сдвиг. Например, если в 1999 г. (i=1) автомобиль имел возраст 4 года (выпущен в 1996 г.), то в 2000 г. (i=1+1=2) его возраст составит 4+1=5 лет.
4 Поставки автомобилей условно относятся к началу, а списание – к концу соответствующего года.
5 Если приобретаются только новые автомобили Апi+1, а списываются автомобили при j=tсп, то дискретное списание называется простым. Количество автомобилей j+1-й возрастной группы в момент i+1 определяется по правилам диагонального сдвига (см. рисунок 3.9) и с учетом этапов существования парка (см. рисунок 3.7).
Для I этапа (при i=t<tсп) в первой возрастной группе j=1 в момент i+1 поступит автомобилей
| Ai+1,1=Aпi+1,1. | (3.16) |
В последующих возрастных группах
| Ai+1,j+1=Aij. | (3.17) |
Списания на этом этапе нет, т.е. Аcпi+1=0.
Для II этапа (при tсп≤i<tк) расчеты проводятся по тем же формулам (3.16) и (3.17), но дополнительно появляется группа автомобилей подлежащих списанию
| Aспi+1=Ai,tсп. | (3.18) |
Для III этапа tK+tcn≥i>tк поставки новых автомобилей прекращаются: Апi+1,1=0, размеры промежуточных возрастных групп автомобилей определяются по формуле (3.17), а размер списания – по формуле (3.18).
6 Если допускается не только приобретение новых автомобилей (j>1), но и промежуточная продажа при tсп j>1, то дискретное списание является сложным.
При этом количество автомобилей возрастной группы j+1 в момент времени i+1 определяется следующим образом:
| Аi+1,j+1=Аij+Апi+1,j+1-Аспi+1,j+1, j=j(2,tсп), | (3.20) |
где Апi+1,j+1 — поставка в момент i+1 автомобилей возрастной группы 2≤j≤tсп, т.е. не новых, которые суммируются с соответствующей возрастной группой;
Аcпi+1,j+1 — вывод из эксплуатации (продажа, передача в лизинг и т.д.) в момент времени i+1 автомобилей возрастной группы 2≤j≤tcп, которые вычитаются из соответствующей возрастной группы.
Размеры первой возрастной группы при наличии поставок новых автомобилей и размеры списания определяются по формулам (3.16) и (3.18).
Естественно, что в реальных условиях в конкретные моменты i существования парка размеры поставок или списания могут быть равны нулю.
В таблице 3.1 рассмотрены фрагменты трансформации структуры и размеров парка при простом и сложном обновлении для двух временных разрезов i и i+1 и сроков службы изделий tсп=5 лет. Исходная возрастная структура парка (при i=1) зафиксирована во втором столбце таблицы. Структура парка при временном разрезе i+1 и простом обновлении и поставке 8 новых автомобилей приведена в третьем столбце, а структура при сложном обновлении, заключающаяся в приобретении 20 автомобилей третьей возрастной группы Апi+1,3 – в четвертом столбце.
7 Как при простом, так и при сложном списании в каждом временном разрезе количество приобретенных и списанных автомобилей в общем случае (характерном для реальной практики) не одинаково, т.е. Аi п≠Аiсп.
8 Размер парка определяется суммированием всех данных по столбцам таблица 3.1:
Таблица 3.1 – Фрагмент расчета простого и сложного дискретного обновления парка
| Параметр | i | i+1 | |
| Простое | Сложное | ||
| Размер поставок Ап | Апi+1,1=+8 | Апi+1,3=+20 | |
| Возрастная группа j (середина интервала), годы 1 (0,5) 2 (1,5) 3 (2,5) 4 (3,5) 5=tсп (4,5) | Аi,1=5 Аi,2=10 Аi,3=12 Аi,4=10 Аi,5=6 | Аi+1,1=8 Аi+1,2=5 Аi+1,3=10 Аi+1,4=12 Аi+1,5=10 | 10+20 |
| Размер списания Асп | Аспi+1,tсп=-6 | -6 | |
| Размер парка А | 5+10+12+10+ +6=43 | 43+8-6=45 | 43+20-6=57 |
| Средний возраст автомобиля Тi, лет | 2,54 | 2,75 | 2,98 |
| Относительный доход парка, % | 98,2 | 123,6 |
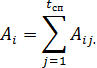
| (3.20) |
9 Прогнозирование возрастной структуры парка позволяет определить по формулам (2.3) и (3.19) динамику изменения реализуемого показателя качества парка по показателям качества автомобилей различных возрастных групп. Так, если доходы автобусов разных возрастных групп парка определяются в процентах Д1=100; Д2=99; Д3=82; Д4=64; Д5=41, то доход парка, являющийся одним из реализуемых показателей качества парка автобусов в момент i (см. таблица 3.1), с учетом возрастной структуры составляет
Дi=  Дjaij=
Дjaij= 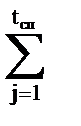 ДjAij/Ai=100·5/43+99·10/43+82·12/43+64·10/43+41·6/43=78,1 %
ДjAij/Ai=100·5/43+99·10/43+82·12/43+64·10/43+41·6/43=78,1 %
относительно дохода (100 %) новых автобусов (j=1).
При временном разрезе i+1 и простом восстановлении средний доход автомобиля парка Дi+1=73,2 %, т.е. на 4,9 % ниже, чем при исходной структуре i. При представленном в таблице 3.1 варианте сложного обновления (приобретении автобусов не новых, а третьей возрастной группы) реализуемый показатель качества по доходам парка будет еще ниже и составит 72,6 % от доходов Дi=100 % автобусов первой возрастной группы, хотя общий доход в результате роста парка возрастает.
10 Средний возраст автомобилей парка Ti, определяется по формуле
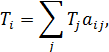
| (3.21) |
где Tj — середина интервала j-й возрастной группы автомобилей.
Для разреза i имеем (см. таблицу 3.1)
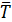 i=0,5·5/43+1,5·10/43+2,5·12/43+3,5·10/43+4,5·6/43=2,54 года.
i=0,5·5/43+1,5·10/43+2,5·12/43+3,5·10/43+4,5·6/43=2,54 года.
Для разреза i+1 и простого обновления
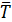 i+1=0,5·8/43+1,5·5/43+2,5·10/43+3,5·12/43+4,5·10/43=2,75 года.
i+1=0,5·8/43+1,5·5/43+2,5·10/43+3,5·12/43+4,5·10/43=2,75 года.
Для того же разреза и сложного обновления парка (поставкой 20 автомобилей третьей возрастной группы) средний возраст парка будет еще выше: 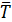 i+1=2,98 года. Это существенно увеличивает затраты на его содержание.
i+1=2,98 года. Это существенно увеличивает затраты на его содержание.
11 Относительный доход парка в расчетных единицах (ре)
| МД=ДiАi. | (3.22) |
По вариантам это составит:
— исходный (i) МДi=43·78,1=335,8 ре (100 %);
— простое обновление (i+1) МДi+1=45·73,2=329,4 ре (98,1 %);
— сложное обновление (i+1) МД1i+1=57·72,6=413,8 ре (123,2 %).
Таким образом, при рассмотренном варианте простого обновления доход парка сократится на 1,9 %, даже при некотором росте размера парка на 4,6 %. При рассмотренном варианте сложного обновления доход парка по сравнению с исходным возрастет на 23,6 % при значительном – на 32,6 % – росте размера парка и его старении, что приведет к существенному увеличению расходов на обеспечение работоспособности этого парка.
3.5.2 Расчет показателей возрастной структуры парка при случайном списании
Этот расчет основан на использовании закономерностей процесса восстановления (закономерности ТЭА пятого вида).
При этом весь наличный парк рассматривается в качестве восстанавливаемой технической системы, состоящей из элементов – отдельных автомобилей. Случайное списание автомобиля в соответствии с законом распределения 2 (см. рисунок 3.8) – это отказ системы, а поставка нового автомобиля, заменившего списанный,— восстановление системы.
Поток замен списываемых автомобилей во время существования парка i описывается, как это было показано ранее, ведущей функцией Ω(i)и параметром потока отказов (списаний) и замен (поставок) ω(i) (см. рисунки 3.4—3.6).
Ведущая функция определяет накопленное число событий (в данном случае – замен списанных автомобилей) к определенной наработке i большой системы – парка автомобилей, формула (3.4). Смысл формулы (3.4) применительно к задаче обновления парка состоит в том, что за фактический календарный срок существования парка автомобилей данной конструкции (i=20—25 лет) будет несколько (k)списаний и замен каждого инвентарного автомобиля (вернее, его гаражного номера).
Рассмотрим последовательность расчета случайного списания при следующих исходных данных: tcп=х=5 лет; σсп=1 год; υсп=σсп/  сп=0,2.
сп=0,2.
Закон распределения случайной наработки до списания – нормальный, что позволяет воспользоваться формулами (3.7) и (3.8).
За интервал календарного времени существования парка принят 1 год, т.е. размер списания и компенсирующей поставки определяется в расчете на 1 год. Расчет проводится для i=16, т.е. 16 календарных лет существования парка. Заданный размер парка, который необходимо поддерживать, Ai=const=100 автомобилей.
Последовательность расчета.
1 Определяем число замен в первом календарном интервале работы парка i=1. Так как фактические наработки при первом списании находятся в интервале  ±3σ, т.е. от 2 до 8 лет, число списаний и замен автомобилей при i=1 Ω(i)≈0, то расчет начинаем с i=2.
±3σ, т.е. от 2 до 8 лет, число списаний и замен автомобилей при i=1 Ω(i)≈0, то расчет начинаем с i=2.
2 При календарном сроке службы парка i+1=2:
а) для первых замен i=2; k=1;  =5; σ=1 и по формуле (3.8)
=5; σ=1 и по формуле (3.8)
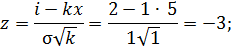
вероятность первых замен F1(2)=Ф(-3)=0,0013 (приложение Б);
б) для вторых замен i=2; k=2;  =5; σ=1.
=5; σ=1.
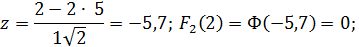
в) так как вероятность вторых замен при i=2 равна 0, то не будет третьих и последующих замен. Поэтому накопленное относительное количество замен на один инвентарный автомобиль при i=2 согласно формуле (3.7) Ω(2)=0,0013+0=0,0013.
3 Подобные расчеты проводятся для i=3, 4, 5,...,16.
Например, для календарной продолжительности работы парка i=8 имеем:
а) для первых замен i=8; k=1;  =5; σ=1:
=5; σ=1:
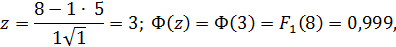
т.е. фактически весь списочный состав парка к этому моменту (i=8) будет обновлен, как минимум, один раз;
б) для вторых замен (k=2)

в) для третьих замен (k=3)
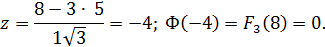
Общее накопленное количество замен на один инвентарный автомобиль за i=8
Ω(8)=F1(8)+F2(8)+F3(8)=0,999+0,082+0=1,081.
Это общее накопленное количество замен в парке на один инвентарный (списочный) автомобиль. Иными словами, за 8 лет существования данного парка каждый списочный автомобиль обновился (списание-замена) в среднем около 1,1 раза.
4 Полученные таким образом накопленные значения сводим в таблицу 3.2.
5 Определяем по формуле (3.13) параметр потока списаний по интервалам календарного периода существования парка (i+1)-i: ω1=Ω(i+1)-Ω(i), так как за интервал расчетов принят 1 год.
6 Число списываемых и, следовательно, получаемых автомобилей по парку при условии Ai=const:
| Аcпi=Апi≈ωiАi. | (3.23) |
Как следовало ожидать (см. рисунки 3.5, 3.6), ω(i)→1/  =ω=1/5=0,2, а Аспi, Апi→20 автомобилям (см. таблицу 3.2).
=ω=1/5=0,2, а Аспi, Апi→20 автомобилям (см. таблицу 3.2).
Однако в начальный период существования парка происходят в полном соответствии с закономерностями процесса восстановления значительные колебания размеров списания и, следовательно, пополнения (рисунок 3.10).
Максимальные потребности в замене (по отношению к средней) возникают в зоне средней наработки для первых замен при i=  +1 (6 лет). Затем амплитуда отклонений ω(i) от ω=const сокращается и в зоне средних для вторых замен (i=11 лет) составляет 135 %, а в зоне средних третьих замен (i=16 лет) – 115 % по отношению к средней.
+1 (6 лет). Затем амплитуда отклонений ω(i) от ω=const сокращается и в зоне средних для вторых замен (i=11 лет) составляет 135 %, а в зоне средних третьих замен (i=16 лет) – 115 % по отношению к средней.
Таблица 3.2 – Определение числа замен в парке автомобилей
| Календарное время работы парка i, годы | Интервал календарного времени Δi, годы | Ω(i) | ω1 | Aспi=Aпi при Ai=100 ед. |
| 0-1 | ||||
| 1-2 | 0,001 | 0,001 | 0,1 | |
| 2-3 | 0,02 | 0,02 | ||
| 3-4 | 0,16 | 0,14 | ||
| 4-5 | 0,50 | 0,34 | ||
| 5-6 | 0,88 | 0,38 | ||
| 6-7 | 0,99 | 0,11 | ||
| 7-8 | 1,08 | 0,09 | ||
| 8-9 | 1,24 | 0,16 | ||
| 9-10 | 1,50 | 0,26 | ||
| 10-11 | 1,77 | 0,27 | ||
| 11-12 | 1,95 | 0,22 | ||
| 12-13 | 2,10 | 0,15 | ||
| 13-14 | 2,30 | 0,20 | ||
| 14-15 | 2,50 | 0,20 | ||
| 15-16 | 2,73 | 0,23 |
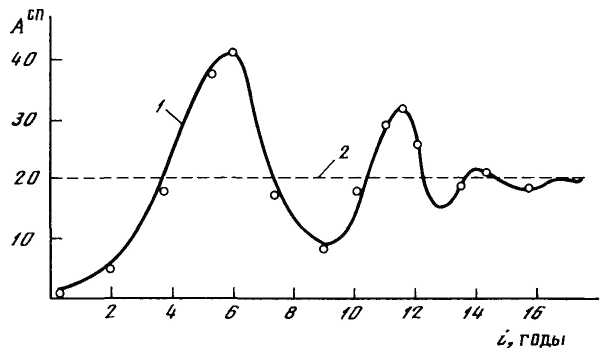
1 — фактическое списание; 2 — списание при ω=const
Рисунок 3.10 – Изменение размеров выбытия (пополнения) парка
при случайном списании
Некоторые практические рекомендации по формированию ВС парка.
1 Возрастная структура парка оказывает существенное влияние на все показатели парка и ИТС, которая обязана анализировать ВС парка и разрабатывать предложения по ее управлению.
Прогноз изменения ВС парка рекомендуется проводить, как минимум, ежегодно. Для внутрихозяйственных расчетов возрастные группы, особенно при различных условиях эксплуатации, целесообразно формировать с меньшим шагом, например в квартал или полгода.
2 Изменение ВС парка зависит от исходной структуры, темпов списания и пополнения, а также установленного срока службы автомобилей. Поэтому применительно к управлению ВС парков недопустимо планирование по достигнутому уровню (размеров списания в предыдущие периоды).
Регулируя списание и пополнение парка, можно получить необходимую возрастную структуру с заданными показателями эффективности, т.е. управлять ими.
3 В разные периоды существования парков они обладают разными провозными способностями, т.е. для выполнения одинаковой транспортной работы количественный состав парков должен изменяться. Для выполнения равной транспортной работы размер парка при его старении должен увеличиваться.
4 Увеличение сроков службы автомобилей до списания без изменения их надежности приводит к существенному ухудшению показателей эффективности парка – средней производительности автомобиля, дохода, коэффициента технической готовности, потребности в рабочей силе, производственно-технической базе (ПТБ), расхода запасных частей. При старении происходят изменения не только количественных, но и качественных показателей работы парков: расширяется номенклатура необходимых запасных частей, материалов; появляется необходимость в выполнении новых видов работ, оборудовании, персонале. Существенно ухудшаются свойства подвижного состава, непосредственно не связанные с надежностью, но влияющие на конкурентоспособность в рыночных условиях: внешний вид, комфортабельность, экологичность и др.
5 Существенного и устойчивого улучшения показателей работы парка можно добиться в результате его омоложения, т.е. своевременного списания автомобилей, выработавших установленный ресурс. Разовые поставки новых автомобилей приводят лишь к временному улучшению показателей по парку в целом, с последующим, более резким ухудшением этих показателей до момента списания этой группы автомобилей.
6 Увеличение темпов обновления парка способствует улучшению показателей эффективности и повышает интенсивность внедрения автомобилей новых конструкций, т.е. способствует научно-техническому прогрессу, но является ресурсоемким мероприятием. В рыночных условиях одним из распространенных и эффективных методов сокращения больших разовых инвестиций при обновлении парков являются различные формы лизинга, т.е. длительной аренды оборудования с рассрочкой соответствующих платежей за его приобретение.
Дата добавления: 2017-08-01; просмотров: 1301;
