Показатели процесса восстановления
1 Наработка до k-гоотказа (восстановления) изделия
| xk=x1+x12+x23+…+xk-1,k. | (3.1) |
Для одного изделия в формуле (3.1) используются фактические значения наработок, а для группы изделий – их средние значения:
 k= 1+Σk k-1,k, k=2, 3, 4, …
| (3.2) |
2 Средняя наработка между отказами для п автомобилей получается из (3.2). Между 1-м и 2-м отказами
12=(Σni=1 12)/n,
между k-1 и k-м
| k-1,k=(Σni=1 k-1,k,)/n.
| (3.3) |
3 Коэффициент полноты восстановления ресурса ηхарактеризует степень сокращения ресурса изделия после ремонта, т.е. качество произведенного ремонта. После первого ремонта (между 1-м и 2-м отказами) η1= 12/ 1 после k-горемонта ηk= k-1,k/ 1.При этом 0≤η≤1.
Сокращение ресурса после первого и последующих ремонтов, которое необходимо учитывать при планировании и организации работ по обеспечению работоспособности, объясняется: частичной заменой только отказавших деталей при значительном сокращении надежности других, особенно сопряженных; нарушением приработки; использованием в ряде случаев запасных частей и материалов худшего качества, чем при изготовлении автомобиля; низким технологическим уровнем работ.
4 Ведущая функция потока отказов (функция восстановления Ω(x) определяет накопленное количество 1-х и последующих отказов изделия к наработке х. Как следует из рисунков 3.3 и 3.4, из-за вариации наработок на отказы происходит смешение отказов, а функции вероятностей 1-х и последующих отказов F1(X), F2(X), ..., Fk(X)частично накладываются друг на друга. Fk(X)– вероятность k-го(1, 2, ..., k)отказа при наработке изделия X.
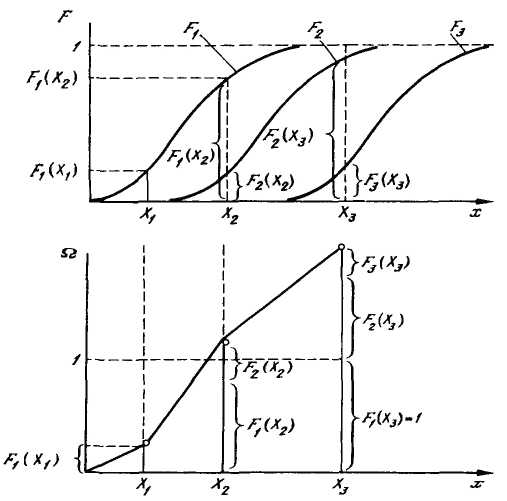
Рисунок 3.4 – Формирование ведущей функции восстановления
| Количество отказов при наработках | Произошли |
| X1: Ω(X1)=F1(X1) X2: Ω(X2)=F1(X2)+F2(X2) X3: Ω(X3)=F1(X3)+F2(X3)+F3(X3) | только 1-е отказы. 1-й и 2-й отказы. 1-, 2- и 3-й отказы. |
| В общем виде |
| Ω(X)=Σ∞k=1Fk(X). | (3.4) |
5 Параметр потока отказов (требований) ω(х) – это плотность вероятности возникновения отказа восстанавливаемого изделия, определяемая для данной наработки (момента времени или пробега):
| ω(x)=dΩ(X)/dx=Σ∞k=1fk(x), | (3.5) |
где fk(х) — плотность вероятности возникновения k-гоотказа.
Иными словами, ω(х)—это относительное число отказов, приходящееся на единицу времени или пробега одного изделия (рисунок 3.5).
В общем случае параметр потока отказов непостоянен во времени, т.е. ω(t, х)≠const. Наблюдаются три основных случая поведения параметра по наработке.
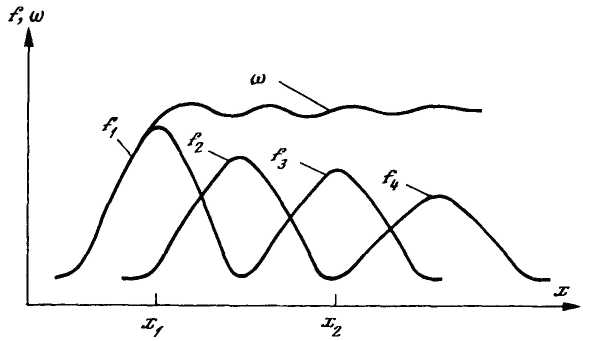
Рисунок 3.5 – Формирование параметра потока отказов
Первый случай (рисунок 3.6, а, кривая 1) – полное восстановление ресурса после каждого отказа, т.е.
1= 12= 23=…= k-1,k=const, η=1.
При этом происходит стабилизация параметра потока отказов на уровне ω1=1/ 1.
Второй случай (рисунок 3.6, а, кривая 2) — неполное, но постоянное восстановление ресурса после 1-го отказа, т.е.. 1>ηi=const. Для этого случая также характерна стабилизация параметра потока отказов, но на более высоком уровне: ω2=1/(η 1)=const.
Третий случай (рисунок 3.6, а,кривая 3)—последовательное снижение полноты восстановления ресурса, т.е. ηi≠const, 1>η1>η2>…>ηk.
В этом случае и параметр потока отказов непрерывно увеличивается, что приводит к постоянному повышению нагрузки на ремонтные подразделения предприятия. Однако при расчетах для этого случая можно принимать ω=const как среднюю для отдельных периодов I, II и III, на которые разбивается весь пробег или время работы автомобиля. Подобный подход возможен также при анализе изменения параметра потока отказов в течение года (рисунок 3.6, б). В этом случае также можно принимать ω практически постоянным для зимнего (ω3), осенне-весеннего (ω0, ωв) и летнего (ωл) периодов.
а — по наработке с начала эксплуатации; б — сезонное
Рисунок 3.6 – Изменение параметра потока отказов
Дата добавления: 2017-08-01; просмотров: 945;