Показатели надежности сложных систем
Под системой понимается совокупность элементов или подсистем, находящихся во взаимодействии и образующих определенную общность. Автомобиль (система) состоит из ряда подсистем (агрегатов), которые, в свою очередь, состоят из элементов (деталей).
Содержание и режимы проведения профилактических и ремонтных работ, как правило, адресны и определяются надежностью элементов: провести смазку конкретного соединения или узла; проверить затяжку конкретного крепежного соединения; отрегулировать зазор (люфт, ход) конкретного механизма, заменить конкретную деталь или агрегат и т.д.
Надежность системы (которую необходимо знать для оценки качества и эффективности системы, а также планирования и организации ТО и ремонта) определяется надежностью составляющих элементов и структурой системы, т.е. способами соединения и взаимодействия элементов.
Показатели надежности систем определяются следующими методами.
1 По результатам эксплуатации систем (в процессе которой фиксируются отказы и неисправности) рассчитывают для системы некоторые показатели надежности и оценивают вклад в ее формирование отдельных подсистем или элементов автомобиля (таблица 2.6). Полученные таким образом данные используются для корректирования технологии и организации ТО и ремонта с учетом надежности элементов систем, а также предъявления требований к производителям автомобилей и выбору последних.
2 На основании аналитических расчетов надежности системы по надежности ее элементов. Такие расчеты строятся на структурной схеме системы, определяющей связи между элементами, и данных по законам распределения показателей надежности элементов.
Преимущества аналитических расчетов – возможность количественно оценить влияние элемента на надежность системы. Однако аналитические расчеты возможны для ограниченного перечня законов распределения (экспоненциальный и в меньшей степени нормальный и логарифмически нормальный), и их сложность существенно возрастает при росте числа элементов в системе.
3 Если законы распределения показателей надежности элементов неизвестны или для них отсутствует аналитический аппарат, а также для систем с большим числом различных элементов применяются методы имитационного моделирования. При этом в основе модели – также данные по надежности элементов и структурная схема системы.
Таким образом, два из трех рассмотренных методов основываются на построении структурной схемы системы, основой которой являются связи или соединения между элементами.
Эти соединения могут быть последовательными, параллельными или смешанными, представляющими комбинации первых двух (рисунок 2.7).
Таблица 2.6 – Распределение отказов автобусов среднего класса
| Элемент (агрегат, система) | Число отказов, % | Трудоемкость устранения | Затраты на запасные части, % | Простой в ремонте, % | |
| средняя отказов, чел.-ч | отказов, % | ||||
| Двигатель | 17,7 | 3,5 | 37,7 | 42,1 | 36,9 |
| Система питания | 2,5 | 1,0 | 1,5 | 1,8 | 2,4 |
| Система выпуска | 3,3 | 0,6 | 1,3 | 1,3 | 1,5 |
| Система охлаждения | 8,8 | 2,1 | 11,4 | 12,4 | 11,2 |
| Сцепление | 6,3 | 1,6 | 6,4 | 1,4 | 4,9 |
| Коробка передач | 5,6 | 2,2 | 7,5 | 5,8 | 6,7 |
| Карданная передача | 5,0 | 1,2 | 3,8 | 5,2 | 3,6 |
| Задний мост | 1,4 | 1,6 | 1,4 | 0,1 | 2,8 |
| Подвеска | 4,9 | 1,3 | 4,1 | 7,4 | 4,4 |
| Передний мост | 4,6 | 1,9 | 5,5 | 3,6 | 3,6 |
| Колеса и ступицы | 0,6 | 2,1 | 0,8 | 0,8 | 0,8 |
| Рулевое управление | 2,0 | 0,5 | 0,7 | 0,9 | 0,8 |
| Тормозная система | 5,5 | 1,7 | 5,7 | 4,3 | 6,0 |
| Электрооборудование и приборы | 10,7 | 0,6 | 4,4 | 5,9 | 5,6 |
| Прочее | 21,1 | – | 7,8 | 7,0 | 7,8 |
| Примечание – Наработка 200 тыс. км |
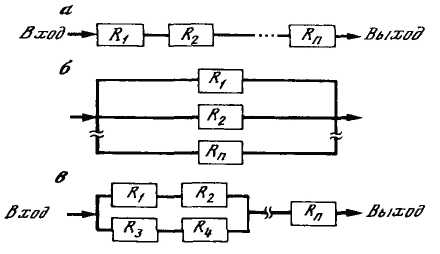
Ri — вероятность безотказной работы i-го элемента
Рисунок 2.7 – Схемы последовательных (а), параллельных (б) и смешанных (в) соединений системы
Рассмотрим влияние связей между элементами на надежность системы.
При последовательном соединении, наиболее распространенном в конструкции автомобилей и других преимущественно механических систем, отказ любого элемента вызывает отказ самой системы. Если отказы элементов независимы, то вероятность безотказной работы системы при последовательном соединении ее элементов Rспс за наработку х определяется произведением вероятностей безотказной работы ее элементов Ri(х)за ту же наработку:
| Rспс(x)=R1(х) R2(х)… Ri(х)… Rn(х)=Пi=1nRi(х). | (2.4) |
Например, для системы, состоящей из четырех последовательно соединенных элементов, у которых за определенную наработку R1=0,98; R2=0,65; R3=0,88 и R4=0,57, вероятность безотказной работы за ту же наработку равна Rспс=0,98 0,65 0,88 0,57=0,32. Иными словами, надежность системы с последовательно соединенными элементами ниже надежности самого слабого ее звена. Поэтому при усложнении конструкции автомобиля, его агрегатов и систем, одним из проявлений которого является увеличение числа элементов в системе, требования к надежности каждого элемента и их равнопрочности резко возрастают.
Вероятность отказа системы как противоположного отсутствию отказа события определяется по формуле
| Fспс(x)=1-Rспс(x). | (2.5) |
В общем случае для любого закона распределения
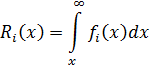
или
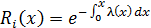 , ,
| (2.6) |
где f(x) и λ(х) — соответственно плотность вероятности отказа и интенсивность отказов i-го элемента.
Если отказы элементов подчиняются экспоненциальному закону распределения, то вероятность безотказной работы системы определяется следующим выражением:
| Rспс=exp(-λ1x) exp(-λ2x)… exp(-λnx)=exp[-(λ1+λ2+…+λn)x]=exp(-xΣni=1λi). | (2.7) |
Следовательно, для определения Rспс необходимо сложить интенсивности отказов всех последовательно соединенных элементов, умножить эту сумму на интересующую наработку и определить вероятность безотказной работы системы.
Характерным примером отказа автомобиля (системы) из-за отказа одного из последовательно соединенных в надежностном смысле элементов (шины) является прекращение движения автомобиля для замены колеса или ремонта шины из-за случайного ее прокола или повреждения, вероятность которого подчиняется экспоненциальному закону.
Определим вероятность дорожного прокола шины легкового автомобиля-такси за наработку в течение смены х=lсс=300 км.
Согласно отчетным данным, по этой причине интенсивность отказа шины переднего колеса λп=0,03 (тыс. км)-1; заднего колеса λз=0,04 (тыс. км)-1;
Интенсивность дорожного отказа автомобиля по этой причине Δ=
=2 0,03+2 0,04=0,14 (тыс. км)-1. Вероятность безотказной работы автомобиля в течение смены
Rспс=exp(-0,3 0,14)=0,958.
Это означает, например, что из ста автомобилей в течение смены могут получить проколы шин примерно четыре автомобиля.
Рассмотрим систему, состоящую из трех последовательно соединенных элементов, имеющих интенсивность отказов соответственно λ1=0,01, λ2=0,015, λ3=0,02 (тыс. км)-1. Для системы согласно формуле (2.7) λΣ=0,045, а средняя наработка на отказ хс=22,2 тыс. км. Вероятность безотказной работы этой системы за сменную наработку (150 км) составляет Rспс(х=0,15 тыс. км)=ехр(-0,15·0,045)≈0,995, а за наработку между последовательно проводимыми ТО (lто=3 тыс. км) Rсп (х=3 тыс. км)=ехр(-0,135)=0,875.
В результате конструктивного совершенствования система получила два дополнительных элемента с λ4=0,005 и λ5=0,008, и ее показатели изменились следующим образом:
— средняя наработка на отказ – 17,2 тыс. км, т.е. на 30 % ниже, чем при прежней конструкции;
— вероятность отказа за сменную наработку – 0,91;
— то же за межосмотровой период – 0,84.
Для получения прежних показателей средняя наработка на отказ каждого элемента системы должна быть увеличена на 23—25 %.
При параллельном соединении, где каждый из элементов выполняет одинаковые функции, отказ системы может произойти при отказе всех элементов за наработку х. Использование в конструкции системы параллельно соединенных элементов является резервированием, которое может быть нагруженным и ненагруженным.
При нагруженном (горячем) резервировании все элементы (основной и резервный) работают в течение всего времени в одинаковом режиме. Вероятность отказа системы при этом
| Fспс(x)=Пni=1Fi(x), | (2.8) |
а безотказной работы
| Rспс(x)=1-Fспс(x). | (2.9) |
Например, при F1(x)=0,2 и F2(x)=0,15 (R1(x)=0,8; R2(x)=0,85) вероятность отказа системы Fспр(x)=0,2 0,15=0,03, а вероятность безотказной работы системы Rспр(x)=0,97, т.е. выше вероятности безотказной работы любого из элементов системы.
Таким образом, надежность системы с параллельным соединением элементов выше, чем надежность любого входящего в систему элемента.
Если резервные элементы подключаются к работе по мере отказов основных, то резервирование называется ненагруженным или холодным. Наиболее простой случай – это система, состоящая из основного рабочего и резервного элементов. В этой схеме рабочий элемент отказывает при случайной наработке системы x1 а наработка резервного элемента начинается с момента х2=х-x1. Наработка на отказ системы для произвольных (известных) законов распределения наработки на отказы рабочего f1(x1) и резервного f2(x2) элементов определяется функцией
| fспр(x)=∫x∞ f1(x1) f2(x2)dx, | (2.10) |
а вероятность безотказной работы системы
| Rспс(x)=∫x∞ fспр(x)dx. | (2.11) |
Для экспоненциального закона распределения
| Rспс(x)=е-Λ1x+RпΛ1(е-Λ1x-е-λ2x)/(λ2-Λ1), | (2.12) |
где Rп— вероятность безотказной работы устройства, переключающего систему с основного элемента на резервный (если оно предусмотрено конструкцией системы).
Наличие запасного колеса описывает схему, в которой цепь из последовательно соединенных в надежностном смысле четырех элементов, имеющих интенсивность отказов в рассмотренном выше примере х=0,3 Λ1=0,14 (тыс. км)-1, резервируется запасным колесом с λзп=0,035 (тыс. км)-1. По формуле (2.12) вероятность безотказной работы автомобиля в течение смены (при Rп=1)
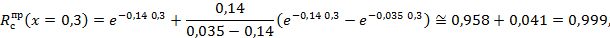
т.е. наличие запасного колеса практически исключает в рассматриваемых условиях отказ автомобиля, связанный с прекращением или нарушением транспортного процесса.
В автомобильных конструкциях иногда дублируются приборы системы зажигания (специальные автомобили и особые условия эксплуатации). К условному резервированию относятся также раздельные приводы тормозной системы. При этом отказ одного контура, в котором последовательно соединены, например, тормозные механизмы переднего левого и заднего правого колеса, частично компенсируется вторым контуром. Полного отказа системы не происходит, но эффективность торможения сокращается. Это так называемый частичный отказ автомобиля, снижающий вероятность возникновения аварийной ситуации при внезапном отказе одного контура.
Имея данные по надежности системы, можно определить по соответствующим формулам гамма-процентные, средние ресурсы, вероятности отказов при различных наработках системы и другие необходимые показатели надежности.
Принципы резервирования используются в ТЭА также при определении запасов, резервного технологического оборудования, персонала и автомобилей, что увеличивает надежность системы, в качестве которой в данном случае выступает ИТС, автотранспортное предприятие или предприниматель, осуществляющий перевозки.
Возникают вопросы: что практически дает информация по надежности и качеству автомобилей, не является ли она избыточной, бесполезной для ТЭА, приводящей к увеличению затрат на эксплуатацию автомобилей? Для чего необходимо специалисту понимание процессов изменения технического состояния автомобилей и умение измерить их количественно?
1 Прежде всего, эти знания помогают выбирать более качественные и надежные автомобили, агрегаты и предъявлять их производителям конкретные и обоснованные требования.
2 Знание того, что безопасность, безотказность, экологичность и экономичность современного автомобиля определяются надежностью сравнительно небольшой группы в 100—300 деталей (1—2 % их общего числа), поможет сосредоточить усилия ИТС эксплуатационных предприятий и производителей автомобилей на обеспечении работоспособности именно этих деталей.
3 Знание номенклатуры этих деталей и их надежности (которые могут изменяться в зависимости от конструкции автомобилей и условий эксплуатации) позволяет ИТС:
— разрабатывать и реализовывать меры по предупреждению отказов и неисправностей;
— знать, какие работы могут возникнуть, т.е. определять и предвидеть возможную производственную программу предприятия;
— иметь соответствующие производственные и складские помещения, персонал и оборудование;
— знать, какие детали и материалы, в каком количестве и какой стоимостью заказывать (см. рисунок 2.6, таблица 2.5) и иметь на складе;
— в соответствии с номенклатурой и вероятной потребностью деталей и материалов можно реализовывать рациональные схемы материально-технического обеспечения.
4 Понимание закономерностей изменения технического состояния позволяет перейти от ожидания отказов к их предотвращению, т.е. отслеживать и управлять неизбежными при случайных процессах рисками.
5 Достоверная информация позволяет нормировать процессы технической эксплуатации и управлять ими на основе системы технического обслуживания и ремонта автомобилей, упорядочить взаимоотношения с клиентурой ИТС как внутри, так и вне предприятия, а также с государственными и местными органами.
6 Опираясь на закономерности ТЭА четвертого вида, можно управлять реализуемыми показателями качества автомобилей и парков в эксплуатации.
Дата добавления: 2017-08-01; просмотров: 2094;
