Тогда волновое уравнение

Физика волновых процессов

Волна, волновая поверхность, волновой фронт, частота волны, скорость волны.

Классификация:

- монохроматические и немонохроматические волны
- механические и электромагнитные волны
- - продольные волны	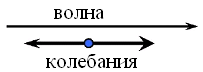- поперечные волны
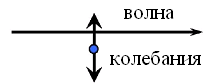
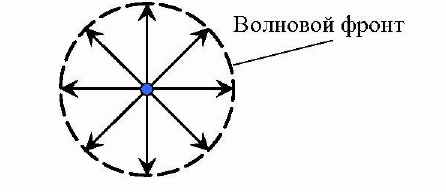
- сферические волны	- плоские волны

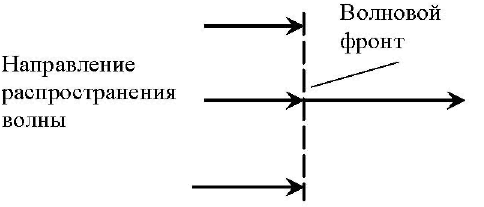
……уравнение бегущей и стоячей волны (нет в конспекте, было изложено)

Исключительно «на перспективу»

Волновое уравнениеимеет следующий вид, оно представляет собой дифференциальное уравнение второго порядка в частных производных

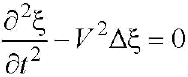или

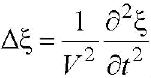
Здесь

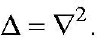К примеру,

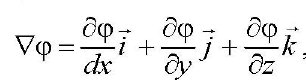
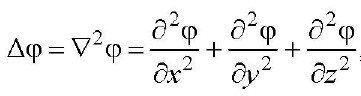, или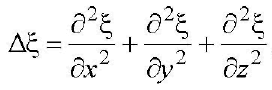

Тогда волновое уравнение

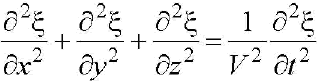
Любая функция вида 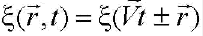является решением волнового уравнения.

Если волна распространяется вдоль одного направления, тогда уравнение становится одномерным волновым уравнением.Одномерное волновое уравнение при рас­пространении волны вдоль оси Ох имеет вид

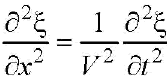
Скорость распространения колебаний, которую мы назвали скоростью волны,является фазовой скоростью волны.Она определяет скорость, с которой перемещается поверхность постоянной (одинаковой) фазы волны.

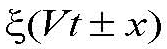- решение одномерного волнового уравнения.

Безразмерный аргумент функции 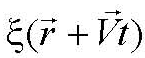, описывающей волновой процесс,

называется фазой волны.

Фаза плоской волны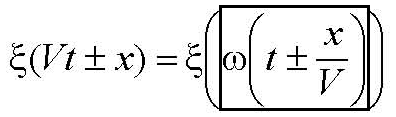

Скорость распространения колебаний, которую мы назвали скоростью волны,является фазовой скоростью волны.Она определяет скорость, с которой перемещается поверхность постоянной (одинаковой) фазы волны.

Минимальное расстояние между двумя точками, в которых фаза колебаний одинакова в один и тот же момент времени, называется длиной волны .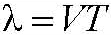

Волна называется гармонической,если распространяющиеся колебания яв­ляются гармоническими.

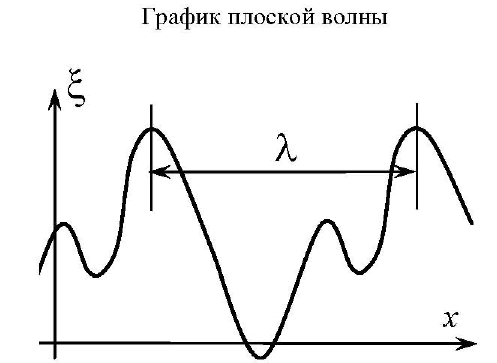
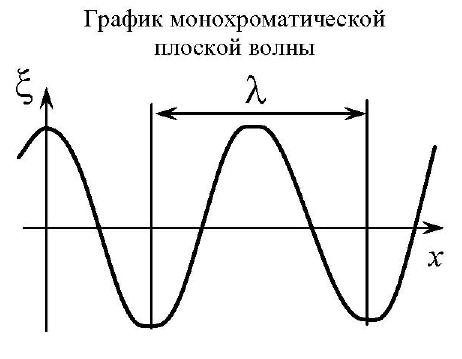
Для гармонических волн вводят понятие амплитуды волны,которая равна амплитуде гармонических колебании в данной точке пространства.

Интенсивностью волныназывается количество энергии, переносимой волной в единицу времени через единичную площадку, перпендикулярную распространению волны.