Простые ставки ссудных процентов
Простые ставки ссудных (декурсивных) процентов применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет, как правило, срок менее одного года), или когда после каждого интервала начисления кредитору выплачиваются проценты. Естественно, простые ставки ссудных процентов могут применяться и в любых других случаях по договоренности участвующих в операции сторон [46, 67–69].
Введем следующие обозначения:
i (%) – простая годовая ставка ссудного процента;
i – относительная величина ставки процентов;
Iг– сумма процентных денег, выплачиваемых за год;
I – общая сумма процентных денег за весь период начисления;
Р – величина первоначальной денежной суммы;
S – наращенная сумма;
kн – коэффициент наращения;
п – продолжительность периода начисления в годах;
д – продолжительность периода начисления в днях;
К – продолжительность года в днях.
Величина К является временной базой для расчета процентов.
В зависимости от способа определения продолжительности финансовой операции рассчитывается либо точный, либо обыкновенный (коммерческий) процент. Дата выдачи и дата погашения ссуды всегда считаются за один день. При этом возможны два варианта.
Вариант 1: используется точное число дней ссуды, определяемое по специальной таблице, где показаны порядковые номера каждого дня года; из номера, соответствующего дню окончания займа, вычитают номер первого дня;
Вариант 2: применяется приблизительное число дней ссуды, когда продолжительность полного месяца принимается равной 30 дням; этот метод используется, когда не требуется большая точность, например, при частичном погашении займа.
Точный процент получают, когда за временную базу берут фактическое число дней в году (365 или 366) и точное число дней ссуды.
Приведенным выше определениям соответствуют формулы:
| i(%) = (Iг /P)100 %. | (11.6) |
| i = Iг /P. | (11.7) |
| I = Iг n. | (11.8) |
| S=P + I. | (11.9) |
| kн = S/P. | (11.10) |
| n = д/К . | (11.11) |
Применяя последовательно формулы (11.9), (11.8), (11.7) и (11.11), получаем основную формулу для определения наращенной суммы:
| S = P(1+ni), | (11.12) |
или
| S = P (1+ (д /K)i). | (11.13) |
Если необходимо узнать величину суммы Р, которая в будущем должна составить заданную величину S, тогда Р называется современной (текущей, настоящей приведенной) величиной суммы S. Определение современной величины Р наращенной суммы S называется дисконтированием, а определение величины наращенной суммы S – компаудингом [45, 69, 80, 83].
Из формулы (11.12) получаем формулу, соответствующую операции дисконтирования:
| P = S/(1+ni). | (11.14) |
Преобразуя формулу (11.12) получаем еще несколько формул для определения неизвестных величин в различных случаях:
| n = (S-P)/Pi. | (11.15) |
| д = (S -P) K/ Pi. | (11.16) |
| i = (S -P)/ Pn. | (11.17) |
| д = (S -P) K/ Pд. | (11.18) |
Иногда на разных интервалах начисления применяются разные процентные ставки. Если на последовательных интервалах начисления n1,n2,.., nN используются ставки процентов i1,i2,.., iN , по формулам (11.7) и (11.8) сумма процентных денег в конце первого интервала составит:
| I1 =Pn1i1, | (11.19) |
в конце второго интервала:
| I2 =Pn2i2. | (11.20) |
При N интервалах начисления наращенная сумма составит:
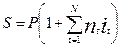 . .
| (11.21) |
Для множителя наращения, следовательно, имеем:
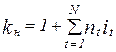 . .
| (11.22) |
Дата добавления: 2017-06-02; просмотров: 493;
