Годовая рента, начисление процентов m раз в году.

Пусть анализируется годовая рента постнумерандо. Однако проценты начисляются mраз в году. Члены ренты с начисленными к концу срока процентами образуют ряд (перепишем его в обратном порядке):

,

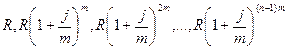где j– номинальная (годовая) ставка процентов.

И в этом случае мы имеем дело с возрастающей геометрической прогрессией. Первый член прогрессии равен R,знаменатель – (1 +j/m)^m.Сумма членов этой прогрессии равна

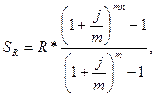
где n – срок ренты.

Пример 4. Найти сумму ренты по данным примера 2, с изменением условий: пусть проценты начисляются поквартально.

Решение:

В этом случае это годовая рента с начислением процентов 4 раза в год, т.е. общее количество начислений составит 5×4 = 20 (раз).

Отсюда сумма всех взносов с начисленными на них процентами будет равна:

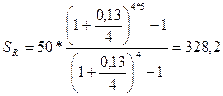тыс.руб.

Отсюда сумма начисленных процентов будет равна:

I = S - P = 328,2 - 250,00 = 78,2 тыс. руб.

Как видим, переход от годового начисления процентов к ежеквартальному начислению заметно увеличил как наращенную сумму, так и сумму процентов.

Пример 5.Найти сумму ренты по данным примера 2, с изменением условий: проценты начисляются ежемесячно.

Решение:

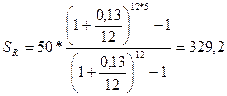
I = S - P = 329,2 - 250,00 = 79,2 тыс. руб.